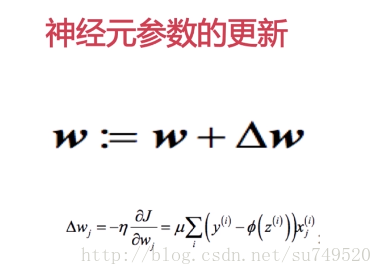自適應線性神經網路(Adaline)和感知器的區別：

1.自適應線性神經網路的啟用函式不再採用步調函式，而是直接將樣本運算的結果（點乘）與實際結果相比較。(白話版：自適應線性神經網路的啟用函式，是一個線性函式)

2.自適應線性神經網路提出了代價函式的概念，並對其做了最小優化。基於Adaline規則的權重更新是通過一個連續的線性啟用函式(本例子中採用)來完成，而感知器採用的單位階躍函式。

相關概念：

距離：和方差公式(歐幾里得距離)：  ，，其中y表示輸入的第i組資料對應的結果。不斷訓練，當這個距離J最小的時候，訓練結束。（注意：這是所有輸出誤差的和，因為本次距離只採用一個神經元，所以只有一個輸出，沒有用到求和公式）

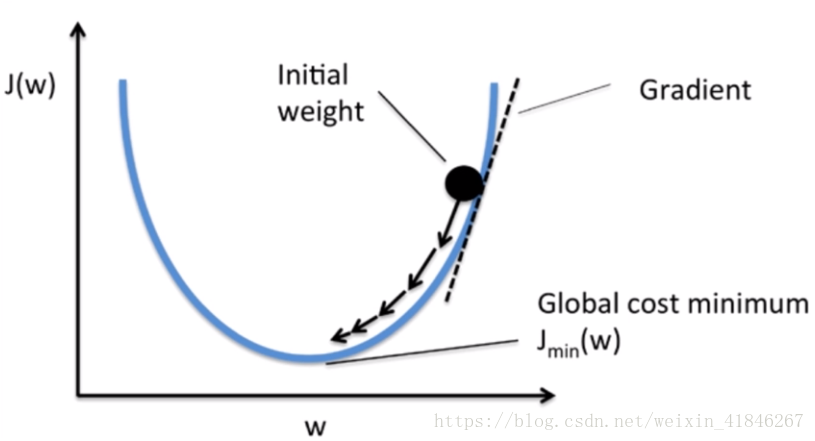
漸進下降法：和方差的函式實際上是一條曲線，對J(w)求導數，當大於0的時候，減小W，當小於0的時，增加W，這個方法叫漸進下降法。

步驟：

（有監督學習的核心：定義一個待優化的目標函式，即做最小化處理的代價函式。）

1.Adaline將和方差公式作為代價函式

2.通過梯度下降演算法，沿梯度做權重更新。權重增量定義為負梯度和學習速率的乘積。

（求偏導的過程，可以理解為權重w對誤差結果的影響程度，也就是斜率，斜率越大，影響越大。更新過程就是權重W減去學習速率*總誤差關於權重W的斜率。同理，偏置b的更新實際上就是偏置b減去學習速率*總誤差關於偏置b的斜率）

（注意：之所以第二個求和符號會沒有，是因為對樣本向量中的某一個樣本值求和，就是它本身）

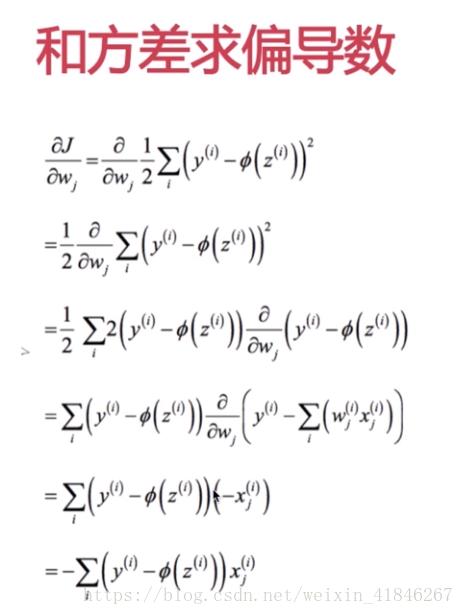
自適應性神經元和感知器的最大區別在於啟用函式的不同。