神經網路學習(一)——感知器分類演算法
最近,學習了一下神經網路的相關知識。寫一篇部落格,做思路整理。
神經網路包含input layer、hidden layer、output layer三層。(考慮真實神經原傳輸訊號的過程)
感知器分類演算法只適用於可以線性分割的資料!!!!!
相關概念:
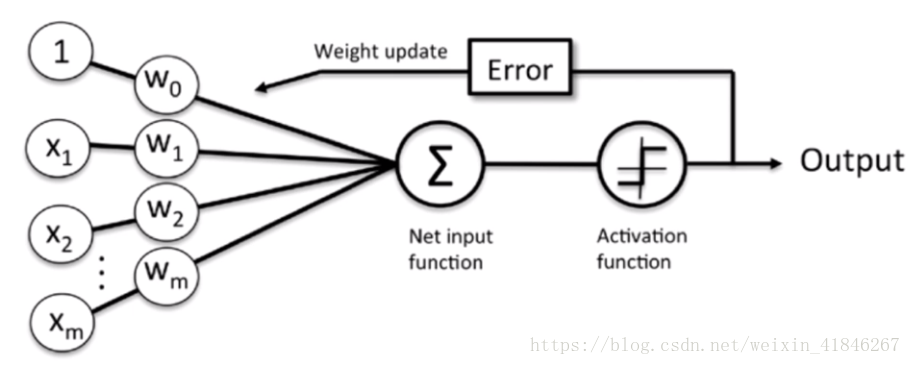
訓練樣本X = ,權重向量W =
,
(這個過程叫向量的點乘)。
啟用函式(單元步調函式):,用來分類。(注意,這是一個線性啟用函式)
閾值(偏置):,初始的閾值根據“經驗”給出,隨著模型的訓練,會更新
學習速率:,是0到1比區間內的小數
步驟:
1.把權重向量初始化為0,或把每一個分量初始化為0到1間的任意小數。(
2.把訓練樣本輸入感知器,得到分類結果(-1或1)
3.根據分類結果更新權重向量和閾值。
權重更新演算法:
y是輸入樣本的正確分類,是感知器計算出來的分類。
閾值更新方法:
整體思路圖如下:
相關推薦
神經網路學習(一)——感知器分類演算法
最近,學習了一下神經網路的相關知識。寫一篇部落格,做思路整理。 神經網路包含input layer、hidden layer、output layer三層。(考慮真實神經原傳輸訊號的過程) 感知器分類演算法只適用於可以線性分割的資料!!!!! 相關概念: 訓練樣本X
第2章 感知器分類演算法 2-2 感知器分類演算法
每一個神經元通過它的分叉組織去接受多個電訊號,而每一個分叉會將電訊號先做一些處理,也就是把這個傳入的電訊號乘以一個引數,所以分叉對應的引數就可以組成一個向量,我們稱之為權重向量W。那麼輸入的電訊號又可以組成一個向量,我們把輸入的電訊號所組成的這個向量稱之為訓練樣本X。 整個機器學習的最終目的,就是通過這個輸
第2章 感知器分類演算法 2-1 分類演算法的總體描述
機器學習的本質是模擬人的神經元對資訊的處理方法。根據神經學的研究,神經元可以看做是一種簡單的帶有二進位制輸出功能的邏輯電路門。多種電訊號能夠從神經元的交叉部分,這種電訊號能夠從交叉部分輸入到我們的神經元之中。那麼這些從這個交叉部分輸進來的電訊號,那麼會進入到神經元的細胞核。那麼細胞核就會將樹突傳入來的這個
神經網路之:感知器
在神經網路中,我們主要使用的是一種稱為S型神經元的神經元模型。感知器就是我們所謂的“人工神經元”。那麼感知器怎麼工作的呢,接下來我們來談談。 1.感知器工作機制: 上圖中有x1,x2和x3輸入,一般情況下我們可以引入權重w1,w2和w3來表示輸入對輸出的重要性,這時可以計算
神經網路基礎和感知器
神經元的變換函式 從淨輸入到輸出的變換函式稱為神經元的變換函式,即 閾值型變換函式比如符號函式 非線性變換函式比如單極性Sigmoid函式 又比如雙極性S型(又曲正切)函式 分段性變換函式比如 概率
神經網路1.3-感知器收斂定理
1.為了誤差修正學習演算法,我們對感知器的模型略作修改:偏置b(n)被當作一個等於1的固定輸入量所驅動的突觸權值。因此我們得到(m+1)×1的輸入向量 , 這裡n表示使用演算法時的迭代步數。 相應的定義(m+1)×1的權值向量: 。 因此,線性組合器的輸出(誘導區域性域)可
神經網路/多層感知器(MLP)架構:選擇隱藏層數量和大小的標準
隱藏層個數: 一個零隱藏層的模型可以解決線性可分資料。所以除非你早知道你的資料線性不可分,證明它也沒什麼壞處—為什麼使用比任務需求更困難的模型?如果它是線性可分的那麼一個更簡單的技術可以工作,感知器也可以。 假設您的資料確實需要通過非線性技術進行分離,則始終
感知器分類演算法
1、基本介紹 感知器學習演算法是神經網路中的一個概念,單層感知器是最簡單的神經網路,輸入層和輸出層直接相連。 每一個輸入端和其上的權值相乘,然後將這些乘積相加得到乘積和,這個結果與閾值相比較(一般為0),若大於閾值輸出端就取1,反之,輸出端取-1。 2
【Python-ML】神經網路-多層感知器增加梯度檢驗
# -*- coding: utf-8 -*- ''' Created on 2018年1月26日 @author: Jason.F @summary: 多層感知器實現,加梯度檢驗 訓練集:http://yann.lecun.com/exdb/mnist/ train-im
神經網路學習引入-線性分類器 Linear Classification
線性分類器 評分函式(score function):計算原始資料到所屬分類的得分 損失函式(loss function):量化預測得分和實際情況之間的認可度 從影象到標籤得分的引數對映 定義評分函式
MATLAB神經網路學習(1):單層感知器
單層感知器由一個線性組合器和一個二值閾值元件組成。 輸入是一個N維向量 x=[x1,x2,...,xn],其中每一個分量對應一個權值wi,隱含層輸出疊加為一個標量值: 隨後在二值閾值元件中對得到的v值進行判斷,產生二值輸出:
【機器學習】神經網路(一)——多類分類問題
一、問題引入 早在監督學習中我們已經使用Logistic迴歸很好地解決二類分類問題。但現實生活中,更多的是多類分類問題(比如識別10個手寫數字)。本文引入神經網路模型解決多類分類問題。 二、神經網路模型介紹 神經網路模型是一個非常強大的模型,起源於嘗試讓機
Spark中基於神經網路的MLPC(多層感知器分類器)的使用
本文首發於我的個人部落格QIMING.INFO,轉載請帶上鍊接及署名。 MLPC(Multilayer Perceptron Classifier),多層感知器分類器,是一種基於前饋人工神經網路(ANN)的分類器。Spark中目前僅支援此種與神經網路有關的演算
系統學習機器學習之總結(一)--常見分類演算法優缺點
主要是參考網上各種資源,做了整理。其實,這裡更多的是從基礎版本對比,真正使用的時候,看資料,看改進後的演算法。 1. 五大流派 ①符號主義:使用符號、規則和邏輯來表徵知識和進行邏輯推理,最喜歡的演算法是:規則和決策樹 ②貝葉斯派:獲取發生的可能性來進行概率推理,最喜歡的演算法是:樸素貝葉
一種用迴歸神經網路學習說話人嵌入的無監督神經網路預測框架
An Unsupervised Neural Prediction Framework for Learning Speaker Embeddings using Recurrent Neural Networks 一種用迴歸神經網路學習說話人嵌入的無監督神經網路預測框架 摘要 本文提出
搭建簡單圖片分類的卷積神經網路(一)-- 訓練模型的圖片資料預處理
一、訓練之前資料的預處理主要包括兩個方面 1、將圖片資料統一格式,以標籤來命名並存到train資料夾中(假設原始圖片按類別存到資料夾中)。 2、對命名好的圖片進行訓練集和測試集的劃分以及圖片資料化。 先對整個專案檔案進行說明: 專案資料夾
神經網路學習引入-鄰近演算法Nearest Neighbor Classifier
鄰近演算法 這個分類演算法與卷積神經網路無關,並且在實際應用中的使用也並不是特別廣泛,但是通過對這個演算法的學習,我們能夠對圖片分類問題有一個大致的解決思路。 L1距離與L2距離 給定的兩個圖片,將它們表現成兩個向量I1、I2,一個最容易理解、最容易被接受的對比它們的方法是L1距
神經網路學習引入-影象分類的基本概述
1. Motivation動機 儘管影象分類聽起來很簡單,但是它在現實中有大量的應用場景。 許多明顯是計算機視覺的任務都可以被簡化成影象分類問題。 2.挑戰 圖片分類問題主要存在的挑戰有: 多視角問題(viewpoint variation):同一個物體的不同角度看到的圖片 大小
深度學習之神經網路(CNN/RNN/GAN)演算法原理+實戰目前最新
第1章 課程介紹 深度學習的導學課程,主要介紹了深度學習的應用範疇、人才需求情況和主要演算法。對課程章節、課程安排、適用人群、前提條件以及學習完成後達到的程度進行了介紹,讓同學們對本課程有基本的認識。 1-1 課程導學 第2章 神經網路入門 本次實戰課程的入門課程。對機器學習和深度學習做了引入
神經網路學習(三)——BP神經網路演算法
前面學習了感知器和自適應線性神經網路。 下面介紹經典的三層神經網路結構,其中每個神經元的啟用函式採用Sigmoid。PS:不同的應用場景,神經網路的結構要有針對性的設計,這裡僅僅是為了推導演算法和計算方便才採用這個簡單的結構。 訓練步驟: 1.正向傳播 2.反向傳播(BP)