推薦：

http://www.cnblogs.com/Booble/archive/2011/02/28/1967179.html

凸包（Convex Hull）是一個計算幾何（圖形學）中的概念。

在一個實數向量空間V中，對於給定集合X，所有包含X的凸集的交集S被稱為X的凸包。

X的凸包可以用X內所有點(X1，...Xn)的線性組合來構造.

在二維歐幾里得空間中，凸包可想象為一條剛好包著所有點的橡皮圈。

用不嚴謹的話來講，給定二維平面上的點集，凸包就是將最外層的點連線起來構成的凸多邊型，它能包含點集中所有的點。

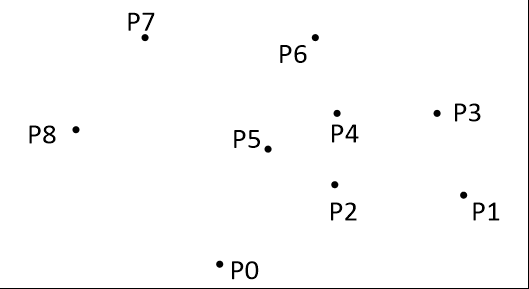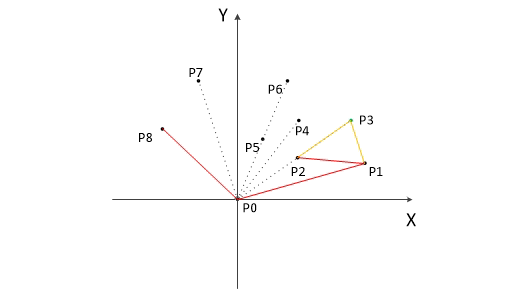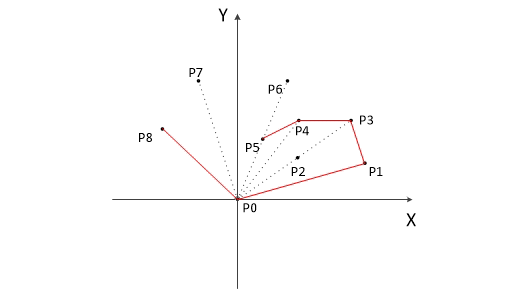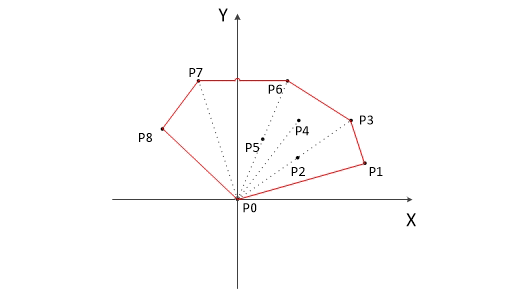
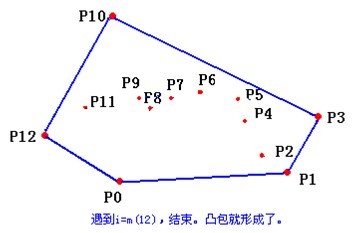
例子：假設平面上有p0~p12共13個點，過某些點作一個多邊形，使這個多邊形能把所有點都“包”起來。當這個多邊形是凸多邊形的時候，我們就叫它“凸包”。如下圖： 

二.解法：

Graham掃描法

時間複雜度：O(n㏒n) 
思路：Graham掃描的思想是先找到凸包上的一個點，然後從那個點開始按逆時針方向逐個找凸包上的點，實際上就是進行極角排序，然後對其查詢使用。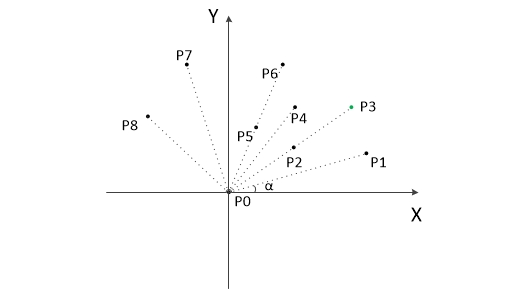 
 
步驟：

1. 把所有點放在二維座標系中，則縱座標最小的點一定是凸包上的點，如圖中的P0。
2. 把所有點的座標平移一下，使 P0 作為原點，如上圖。
3. 計算各個點相對於 P0 的幅角 α ，按從小到大的順序對各個點排序。當 α 相同時，距離 P0 比較近的排在前面。例如上圖得到的結果為 P1，P2，P3，P4，P5，P6，P7，P8。我們由幾何知識可以知道，結果中第一個點 P1 和最後一個點 P8 一定是凸包上的點。 
   （以上是準備步驟，以下開始求凸包）
    
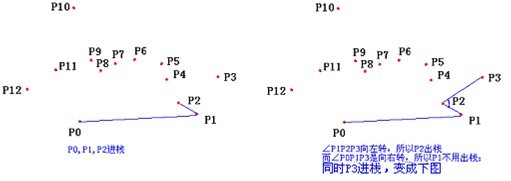
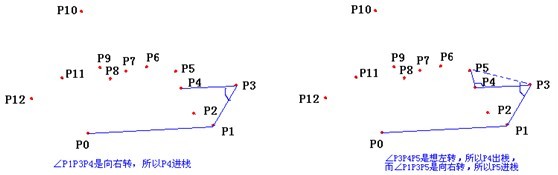
   以上，我們已經知道了凸包上的第一個點 P0 和第二個點 P1，我們把它們放在棧裡面。現在從步驟3求得的那個結果裡，把 P1 後面的那個點拿出來做當前點，即 P2 。接下來開始找第三個點：
4. 連線P0和棧頂的那個點，得到直線 L 。看當前點是在直線 L 的右邊還是左邊。如果在直線的右邊就執行步驟5；如果在直線上，或者在直線的左邊就執行步驟6。
5. 如果在右邊，則棧頂的那個元素不是凸包上的點，把棧頂元素出棧。執行步驟4。
6. 當前點是凸包上的點，把它壓入棧，執行步驟7。
7. 檢查當前的點 P2 是不是步驟3那個結果的最後一個元素。是最後一個元素的話就結束。如果不是的話就把 P2 後面那個點做當前點，返回步驟4。

　　最後，棧中的元素就是凸包上的點了。 
　　以下為用Graham掃描法動態求解的過程： 

　　下面靜態求解過程

三.模板

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define PI 3.1415926535
using namespace std;
struct node
{
    int x,y;
};
node vex[1000];//存入的所有的點
node stackk[1000];//凸包中所有的點
int xx,yy;
bool cmp1(node a,node b)//排序找第一個點
{
    if(a.y==b.y)
        return a.x<b.x;
    else
        return a.y<b.y;
}
int cross(node a,node b,node c)//計算叉積
{
    return (b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y);
}
double dis(node a,node b)//計算距離
{
    return sqrt((a.x-b.x)*(a.x-b.x)*1.0+(a.y-b.y)*(a.y-b.y));
}
bool cmp2(node a,node b)//極角排序另一種方法，速度快
{
    if(atan2(a.y-yy,a.x-xx)!=atan2(b.y-yy,b.x-xx))
        return (atan2(a.y-yy,a.x-xx))<(atan2(b.y-yy,b.x-xx));
    return a.x<b.x;
}
bool cmp(node a,node b)//極角排序
{
    int m=cross(vex[0],a,b);
    if(m>0)
        return 1;
    else if(m==0&&dis(vex[0],a)-dis(vex[0],b)<=0)
        return 1;
    else return 0;
    /*if(m==0)
        return dis(vex[0],a)-dis(vex[0],b)<=0?true:false;
    else
        return m>0?true:false;*/
}
int main()
{
    int t,L;
    while(~scanf("%d",&t),t)
    {
        int i;
        for(i=0; i<t; i++)
        {
            scanf("%d%d",&vex[i].x,&vex[i].y);
        }
        if(t==1)
            printf("%.2f\n",0.00);
        else if(t==2)
            printf("%.2f\n",dis(vex[0],vex[1]));
        else
        {
            memset(stackk,0,sizeof(stackk));
            sort(vex,vex+t,cmp1);
            stackk[0]=vex[0];
            xx=stackk[0].x;
            yy=stackk[0].y;
            sort(vex+1,vex+t,cmp2);//cmp2是更快的，cmp更容易理解
            stackk[1]=vex[1];//將凸包中的第兩個點存入凸包的結構體中
            int top=1;//最後凸包中擁有點的個數
            for(i=2; i<t; i++)
            {
                while(i>=1&&cross(stackk[top-1],stackk[top],vex[i])<0)   //對使用極角排序的i>=1有時可以不用，但加上總是好的
                    top--;
                stackk[++top]=vex[i];                                    //控制<0或<=0可以控制重點，共線的，具體視題目而定。
            }
            double s=0;
            //for(i=1; i<=top; i++)//輸出凸包上的點
            //cout<<stackk[i].x<<" "<<stackk[i].y<<endl;
            for(i=1; i<=top; i++)   //計算凸包的周長
                s+=dis(stackk[i-1],stackk[i]);
            s+=dis(stackk[top],vex[0]);//最後一個點和第一個點之間的距離
            /*s+=2*PI*L;
            int ans=s+0.5;//四捨五入
            printf("%d\n",ans);*/
            printf("%.2lf\n",s);
        }
    }
}

轉自:

https://www.cnblogs.com/aiguona/p/7232243.html