機器學習4---淺談神經網路
1. 神經元模型
神經網路是一個多學科交叉的領域,比較常見的定義是:“”神經網路是由具有適應性的簡單單元組成的廣泛並行互連的網路,它的組織能模擬生物神經系統對真實世界物體做出的互動反應“”。
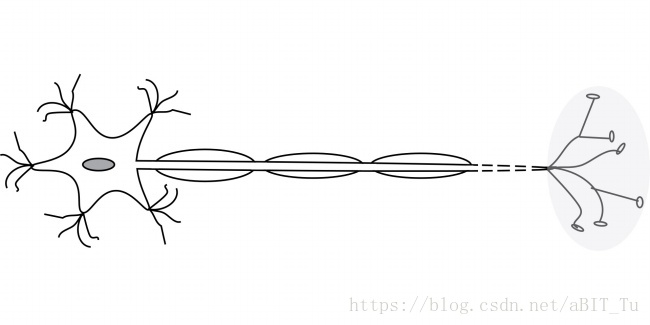
神經網路中最基本的成分是神經元模型,典型的為m-p神經元模型,從生物角度可以形象的理解為下圖。
從模型角度而言,m-p神經元接收n個輸入訊號,並通過權重
連線形成總輸入值,將總輸入值與神經元的閾值
相比較,然後通過啟用函式(activation function)處理以產生神經元的輸出
。
神經網路就是將多個神經元按照一定的層次結構連線起來。
2. 感知器與多層網路
感知器由兩層神經元組成,即輸入層和輸出層。單個感知器通過設定連線權重就可以實現“與”,“或“,”非”等線性問題,兩層感知器可以解決“異或”問題,中間一層叫做隱含層。具體而言,在感知器學習時,將閾值視為“啞節點”,權重總為-1,即可採用“負反饋”的修正思想統一學習權重:,其中
為學習率,控制修正權值的步長。
雖然單個感知器可以有效解決線性可分問題,但是解決非線性可分問題需要使用多層功能神經元,即擁有啟用函式的神經元。更一般的,若每層神經元只與下一層神經元互連,同層或跨層之間沒有互連,則可稱之為“多層前饋神經網路”(multi-layer feedorward neural networks)。
分享一段單個感知器的程式碼段,來源:https://blog.csdn.net/xmu_jupiter/article/details/21884501
function [ w,b ] = original_style( training_set,study_rate ) %training_set是一個m*n維矩陣,其中第一行是y_i,剩下的行的x_i %選取初始值w_0,b_0 w=0; b=0; count=0; %每一次正確分類點個數 iteration_count=0; %迭代次數 fprintf('迭代次數\t誤分類點\t\t權值w\t\t偏置b\t\n');%輸出結果標題 while count ~= size(training_set,2) count=0; %在訓練集中選取資料(x_i,y_i) for i=1:size(training_set,2) count = count+1; %如果y_i(w*x_i+b)<=0,則對w和b進行相應的更新 if training_set(1,i)*(w'*training_set(2:size(training_set,1),i)+b)<=0 w = w + study_rate*training_set(1,i)*training_set(2:size(training_set,1),i); b = b + study_rate*training_set(1,i); iteration_count=iteration_count+1; count=count-1;%不是正確分類點,減一 fprintf('\t%u\t',iteration_count);%輸出迭代次數 fprintf('\t\t%u\t',i);%輸出誤分類點 fprintf('\t(%2.1g,%2.1g)''\t',w);%輸出w fprintf('\t%4.1g\n',b);%輸出b end if w(2,1) ~= 0 x = [-5:0.1:5]; y = (-w(1,1)*x-b)/w(2,1); plot(x, y); pause; end end end end
主函式:
clear all;
training_set=[1,-1,1,-1;3,1,4,2;3,1,3,2];
hold on; xlim([-5,5]);
ylim([-5,5]);
plot(training_set(2,1),training_set(3,1),'*r');
plot(training_set(2,2),training_set(3,2),'*b');
plot(training_set(2,3),training_set(3,3),'*r');
plot(training_set(2,4),training_set(3,4),'*b');
study_rate=1;
[w,b]=original_style( training_set,study_rate );
hold off; 3. 誤差反向傳播(error BackPropagation)
3.1 標準BP演算法和累積BP演算法
BP演算法是迄今最為成功的神經網路學習演算法。為了詳細解釋BP演算法,假設有訓練集D={(xi,yi)| i=1...m},簡單的前饋神經網路只有一層輸入層(d個節點,某一個點為i),一層隱含層(q個節點,某一個點為h),一層輸出層(l個節點,某一個點為j),記輸入層到隱層的某一連線權重為,隱層到輸出層的某一連線權重為
,隱層的某一閾值為
,輸出層的某一閾值為
,隱層的某一節點的輸入值為
,輸出值為
,輸出層的某一節點的輸入值為
,輸出值為
.
如圖:明天來了補圖,今天來不及畫了,有點晚
根據向前傳播的公式可知:
,
(f(*)為啟用函式),
,
(f(*)為啟用函式).
誤差採用均方誤差計算,則有:
向後修正誤差:
基於梯度下降法(gradient descent),即以負梯度方向對目標函式進行調節,則有
,
,
和
類似,
以w的推導為例:
, 其中k表示第k個樣本。
根據鏈式法則,有:
,
容易知道,,記
為輸出層神經元的梯度項,後續可以根據數學求偏導繼續計算,因每一個啟用函式不同而不同
簡單可以寫成,
,
,
, 其中
為隱層神經元的梯度項。
至此標準BP演算法的推導基本結束,總結一下就是:
輸入訓練資料集,確定學習率,隨機初始化連線權重和閾值,開始訓練:
repeat:
對每一個樣本有:
step1. 根據前向傳播公式計算當前樣本的輸出;
step2. 計算輸出層神經元的梯度項;
step3. 計算隱層神經元的梯度項;
step4. 更新連結權重和閾值;
達到終止條件,儲存權重和閾值。
以上是標準BP演算法的步驟和推導,還有一個相像的稱為“累積BP演算法”,它通過計算整個訓練集上的累積誤差進行學習(即每讀取整個訓練集一遍後才更新閾值權重),而非每一個訓練樣本的誤差,因此目標函式為:
,累積BP演算法可以緩解標準BP演算法在準樣本修正中出現的反覆無效修正等問題,但在誤差下降到一定程度後,進一步下降的速度明顯減慢,此時應該選用標準BP演算法。
3.2 處理過擬合
一種策略是“早停”,即將訓練集分為訓練資料集和驗證資料集,當訓練資料集的誤差降低而驗證資料集的誤差上升時,停止訓練,並儲存最小的驗證集對應的權重閾值。
另一種策略是“正則化” (regularization),基本思想是增加一個用於描述網路複雜度的部分,對於誤差和複雜度做以折中,如修正目標函式為,
。
3.3 處理區域性極小
(1)使用多組值初始化。
(2)使用模擬退火演算法,每一步都部分接收次優值。也有使用遺傳演算法的。·
(3)使用隨機梯度下降法,即加入隨機因素,擾亂陷入區域性極小值的可能。