學習筆記-淺談神經網路對信用評級的應用
阿新 • • 發佈:2018-12-29
淺識神經網路在信用評級上的應用
一、一般企業
1.管理風險:金融機構在為中小企業提供貸款時將面臨很大的不確定性和風險,因此在授信前必須對其進行信用評級和風險分析評估
2.成本評估:金融機構需要建立一套完整有效的信用評級機制,來審定中小企業的貸款風險,以幫助作出正確的信貸決策,降低貸前調查和貸後監管的成本
3.企業能力評估:信用評級指標體系的建立應當立足於中小企業本身特點和發展規律,合理並全面的反映影響評價物件信用的所有因素,遵循一致性,系統性,可比性和可測性等原則,從而形成客觀,科學和公正的評估標準和評級方法
二、醫療行業
1.管理風險:確定提供貸款方究竟是政府(含銀行),還是醫院自資,還是第三方金融機構?
2.成本評估:1)醫院自身評估 2)患者經濟能力評估 3)資料來源?數學模型?
3.醫院評估:1)醫院等級->醫院可承受的處理相關疾病的能力 2)科室分類
第三部分:信用評級一般方法
1.專家判斷法:突出的優點是具有較好的靈活性,以及在處理定性指標上的優勢, 但是存在著不連續性和主觀性,評級效率較低、 成本較高
2.財務比率分析:是屬於古典信用分析評估方法,是將各項財務指標作為一個整體,系統、綜合、全面地對貸款人財務狀況進行分析、評價
3.數學建模:基於較為嚴謹的統計模型分析方法,是根據歷史資料庫來構建概率統計模型,主要是一些判別分析模型、違約概率度量模型和違約損失率度量模型
第四部分:淺識神經網路及其企業應用
1.基本原理
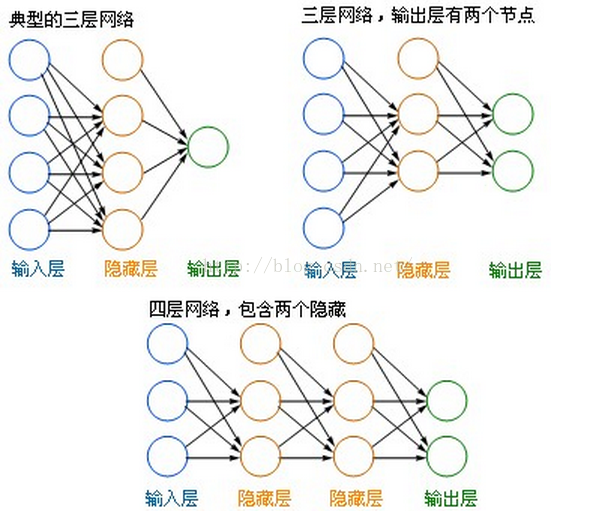 四層
四層
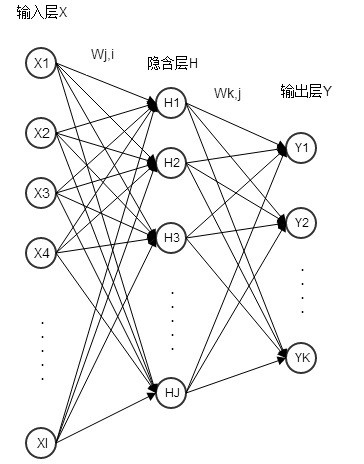
1)左邊藍色的圓圈叫“輸入層”,中間橙色的不管有多少層都叫“隱藏層”,右邊綠色的是“輸出層”。
2)每個圓圈,都代表一個神經元,也叫節點(Node)。
3)輸出層可以有多個節點,多節點輸出常常用於分類問題。
4)理論證明,任何多層網路可以用三層網路近似地表示。
5)一般憑經驗來確定隱藏層到底應該有多少個節點,在測試的過程中也可以不斷調整節點數以取得最佳效果。
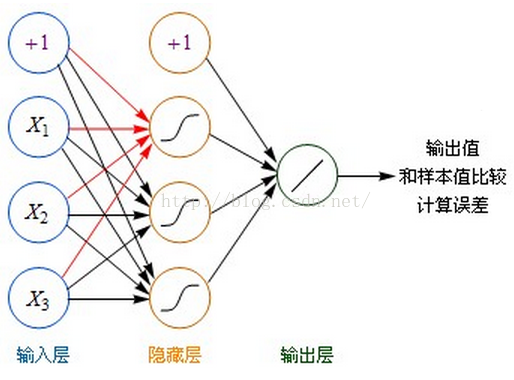
- 雖然圖中未標識,但必須注意每一個箭頭指向的連線上,都要有一個權重(縮放)值。
- 輸入層的每個節點,都要與的隱藏層每個節點做點對點的計算,計算的方法是加權求和+啟用,前面已經介紹過了。(圖中的紅色箭頭指示出某個節點的運算關係)
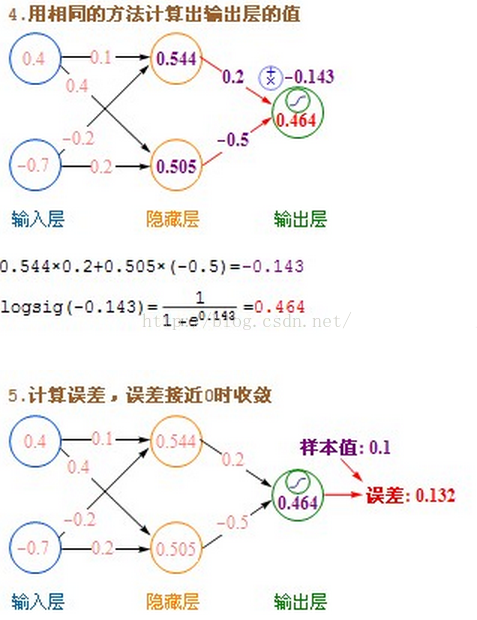
- 利用隱藏層計算出的每個值,再用相同的方法,和輸出層進行計算。
- 隱藏層用都是用Sigmoid作啟用函式,而輸出層用的是Purelin。這是因為Purelin可以保持之前任意範圍的數值縮放,便於和樣本值作比較,而Sigmoid的數值範圍只能在0~1之間。
- 起初輸入層的數值通過網路計算分別傳播到隱藏層,再以相同的方式傳播到輸出層,最終的輸出值和樣本值作比較,計算出誤差,這個過程叫前向傳播(Forward Propagation)。
使用梯度下降的方法,要不斷的修改k、b兩個引數值,使最終的誤差達到最小。神經網路可不只k、b兩個引數,事實上,網路的每條連線線上都有一個權重引數,如何有效的修改這些引數,使誤差最小化,成為一個很棘手的問題。從人工神經網路誕生的60年代,人們就一直在不斷嘗試各種方法來解決這個問題。直到80年代,誤差反向傳播演算法(BP演算法)的提出,才提供了真正有效的解決方案,使神經網路的研究絕處逢生。
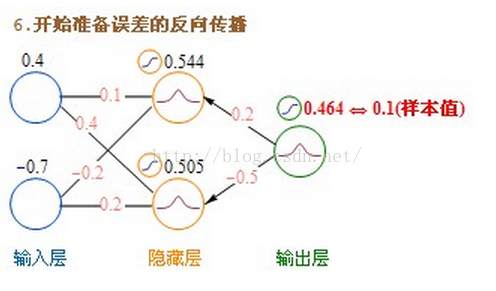
BP演算法是一種計算偏導數的有效方法,它的基本原理是:利用前向傳播最後輸出的結果來計算誤差的偏導數,再用這個偏導數和前面的隱藏層進行加權求和,如此一層一層的向後傳下去,直到輸入層(不計算輸入層),最後利用每個節點求出的偏導數來更新權重。
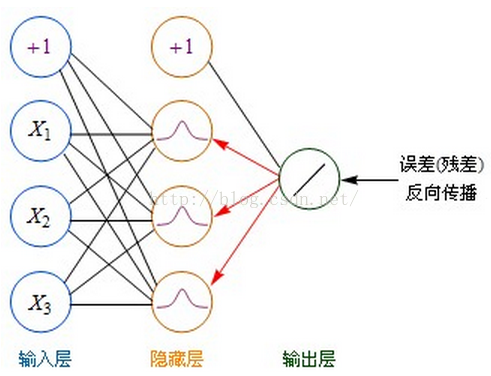
為了便於理解,後面一律用“殘差(error term)”這個詞來表示誤差的偏導數。
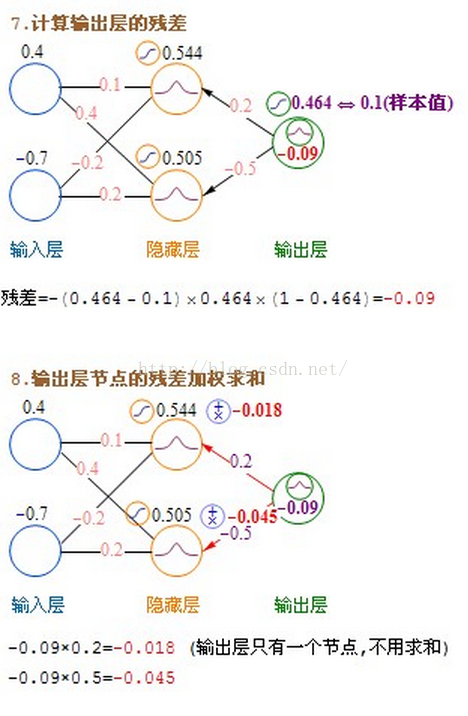
輸出層→隱藏層:殘差 = -(輸出值-樣本值) * 啟用函式的導數
隱藏層→隱藏層:殘差 = (右層每個節點的殘差加權求和)* 啟用函式的導數
例如:如果輸出層用Purelin作啟用函式,Purelin的導數是1,輸出層→隱藏層:殘差 = -(輸出值-樣本值)
如果用Sigmoid(logsig)作啟用函式,那麼:Sigmoid導數 = Sigmoid*(1-Sigmoid)
輸出層→隱藏層:殘差 = -(Sigmoid輸出值-樣本值) * Sigmoid*(1-Sigmoid) = -(輸出值-樣本值)*輸出值*(1-輸出值)
隱藏層→隱藏層:殘差 = (右層每個節點的殘差加權求和)* 當前節點的Sigmoid*(1-當前節點的Sigmoid)
如果用tansig作啟用函式,那麼:tansig導數 = 1 - tansig^2
殘差全部計算好後,就可以更新權重了:
輸入層:權重增加 = 當前節點的Sigmoid * 右層對應節點的殘差 * 學習率
隱藏層:權重增加 = 輸入值 * 右層對應節點的殘差 * 學習率
偏移值的權重增加 = 右層對應節點的殘差 * 學習率
學習率前面介紹過,學習率是一個預先設定好的引數,用於控制每次更新的幅度。
此後,對全部資料都反覆進行這樣的計算,直到輸出的誤差達到一個很小的值為止。
以上介紹的是目前最常見的神經網路型別,稱為前饋神經網路(FeedForward Neural Network),由於它一般是要向後傳遞誤差的,所以也叫BP神經網路(Back Propagation Neural Network)。
BP神經網路的特點和侷限:
- BP神經網路可以用作分類、聚類、預測等。需要有一定量的歷史資料,通過歷史資料的訓練,網路可以學習到資料中隱含的知識。在你的問題中,首先要找到某些問題的一些特徵,以及對應的評價資料,用這些資料來訓練神經網路。
- BP神經網路主要是在實踐的基礎上逐步完善起來的系統,並不完全是建立在仿生學上的。從這個角度講,實用性 > 生理相似性。
- BP神經網路中的某些演算法,例如如何選擇初始值、如何確定隱藏層的節點個數、使用何種啟用函式等問題,並沒有確鑿的理論依據,只有一些根據實踐經驗總結出的有效方法或經驗公式。
- BP神經網路雖然是一種非常有效的計算方法,但它也以計算超複雜、計算速度超慢、容易陷入區域性最優解等多項弱點著稱,因此人們提出了大量有效的改進方案,一些新的神經網路形式也層出不窮。
詳細的計算過程圖:
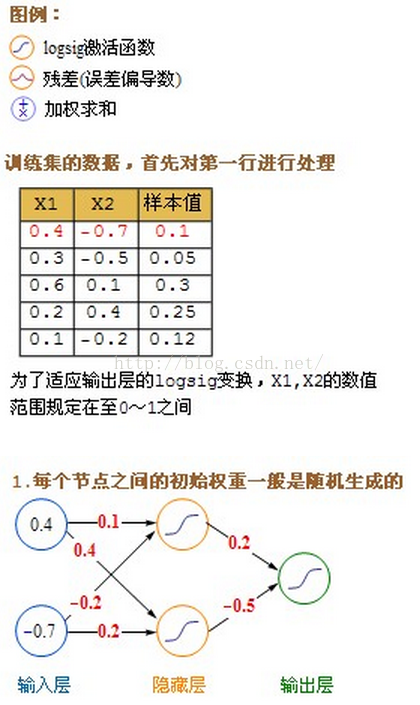
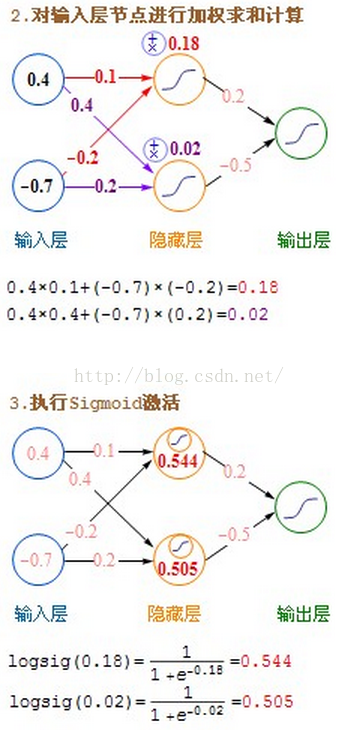



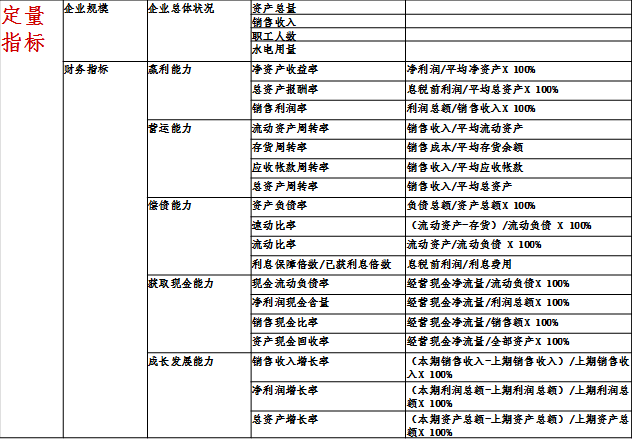
一般企業應用:
2.演算法流程圖
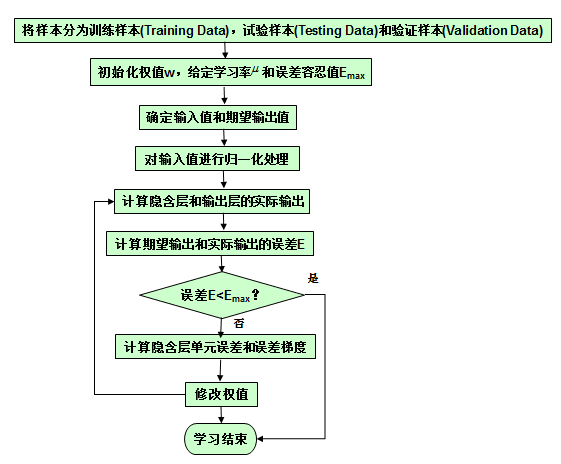
To be continued(醫療輸入輸出變數的假想)
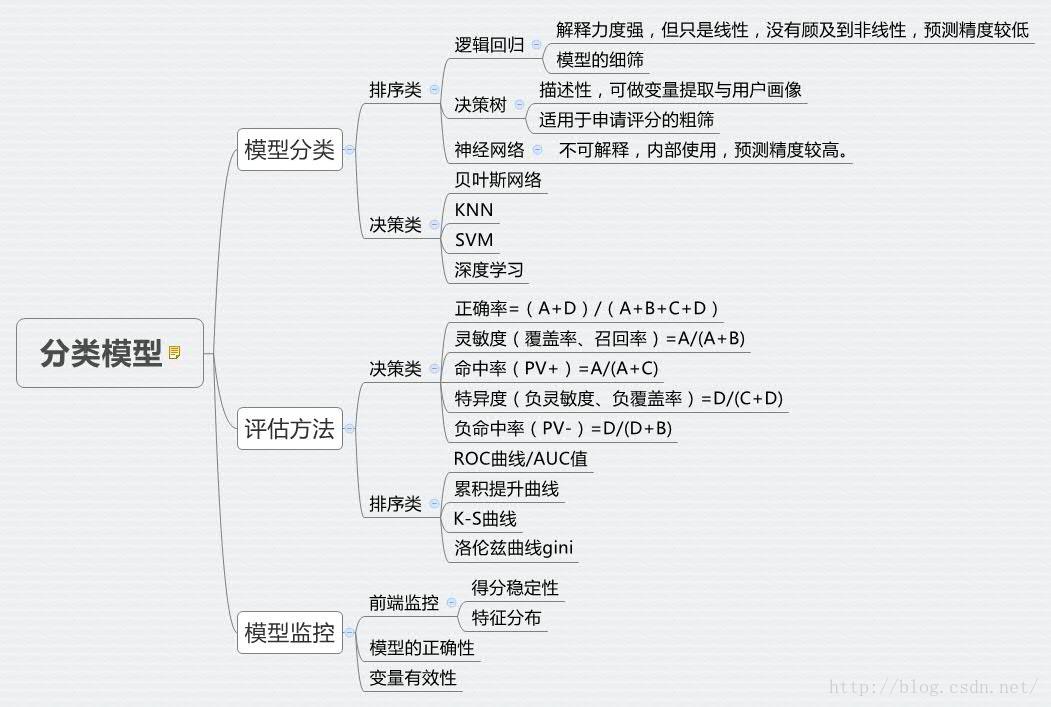
第一部分:常用風控分類模型

第二部分:一般企業對信用評級的要求及醫療行業信用評級的假想
一、一般企業
1.管理風險:金融機構在為中小企業提供貸款時將面臨很大的不確定性和風險,因此在授信前必須對其進行信用評級和風險分析評估
2.成本評估:金融機構需要建立一套完整有效的信用評級機制,來審定中小企業的貸款風險,以幫助作出正確的信貸決策,降低貸前調查和貸後監管的成本
3.企業能力評估:信用評級指標體系的建立應當立足於中小企業本身特點和發展規律,合理並全面的反映影響評價物件信用的所有因素,遵循一致性,系統性,可比性和可測性等原則,從而形成客觀,科學和公正的評估標準和評級方法
二、醫療行業
1.管理風險:確定提供貸款方究竟是政府(含銀行),還是醫院自資,還是第三方金融機構?
2.成本評估:1)醫院自身評估 2)患者經濟能力評估 3)資料來源?數學模型?
3.醫院評估:1)醫院等級->醫院可承受的處理相關疾病的能力 2)科室分類
第三部分:信用評級一般方法
1.專家判斷法:突出的優點是具有較好的靈活性,以及在處理定性指標上的優勢, 但是存在著不連續性和主觀性,評級效率較低、 成本較高
2.財務比率分析:是屬於古典信用分析評估方法,是將各項財務指標作為一個整體,系統、綜合、全面地對貸款人財務狀況進行分析、評價
3.數學建模:基於較為嚴謹的統計模型分析方法,是根據歷史資料庫來構建概率統計模型,主要是一些判別分析模型、違約概率度量模型和違約損失率度量模型
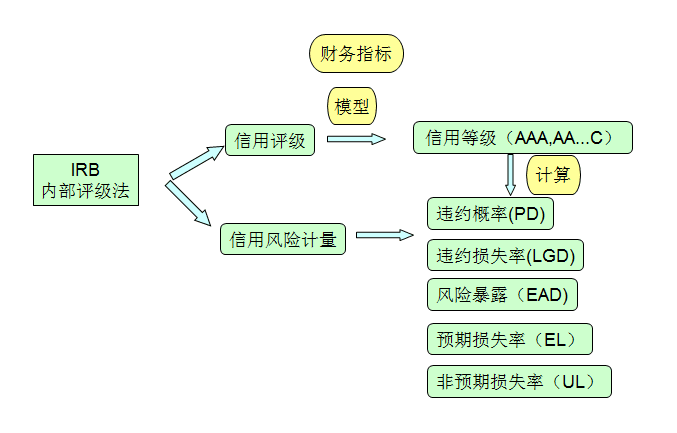
4.IRB:
第四部分:淺識神經網路及其企業應用
1.基本原理
 四層
四層
1)左邊藍色的圓圈叫“輸入層”,中間橙色的不管有多少層都叫“隱藏層”,右邊綠色的是“輸出層”。
2)每個圓圈,都代表一個神經元,也叫節點(Node)。
3)輸出層可以有多個節點,多節點輸出常常用於分類問題。
4)理論證明,任何多層網路可以用三層網路近似地表示。
5)一般憑經驗來確定隱藏層到底應該有多少個節點,在測試的過程中也可以不斷調整節點數以取得最佳效果。
計算方法:

- 雖然圖中未標識,但必須注意每一個箭頭指向的連線上,都要有一個權重(縮放)值。
- 輸入層的每個節點,都要與的隱藏層每個節點做點對點的計算,計算的方法是加權求和+啟用,前面已經介紹過了。(圖中的紅色箭頭指示出某個節點的運算關係)
- 利用隱藏層計算出的每個值,再用相同的方法,和輸出層進行計算。
- 隱藏層用都是用Sigmoid作啟用函式,而輸出層用的是Purelin。這是因為Purelin可以保持之前任意範圍的數值縮放,便於和樣本值作比較,而Sigmoid的數值範圍只能在0~1之間。
- 起初輸入層的數值通過網路計算分別傳播到隱藏層,再以相同的方式傳播到輸出層,最終的輸出值和樣本值作比較,計算出誤差,這個過程叫前向傳播(Forward Propagation)。
使用梯度下降的方法,要不斷的修改k、b兩個引數值,使最終的誤差達到最小。神經網路可不只k、b兩個引數,事實上,網路的每條連線線上都有一個權重引數,如何有效的修改這些引數,使誤差最小化,成為一個很棘手的問題。從人工神經網路誕生的60年代,人們就一直在不斷嘗試各種方法來解決這個問題。直到80年代,誤差反向傳播演算法(BP演算法)的提出,才提供了真正有效的解決方案,使神經網路的研究絕處逢生。
BP演算法是一種計算偏導數的有效方法,它的基本原理是:利用前向傳播最後輸出的結果來計算誤差的偏導數,再用這個偏導數和前面的隱藏層進行加權求和,如此一層一層的向後傳下去,直到輸入層(不計算輸入層),最後利用每個節點求出的偏導數來更新權重。

為了便於理解,後面一律用“殘差(error term)”這個詞來表示誤差的偏導數。
輸出層→隱藏層:殘差 = -(輸出值-樣本值) * 啟用函式的導數
隱藏層→隱藏層:殘差 = (右層每個節點的殘差加權求和)* 啟用函式的導數
例如:如果輸出層用Purelin作啟用函式,Purelin的導數是1,輸出層→隱藏層:殘差 = -(輸出值-樣本值)
如果用Sigmoid(logsig)作啟用函式,那麼:Sigmoid導數 = Sigmoid*(1-Sigmoid)
輸出層→隱藏層:殘差 = -(Sigmoid輸出值-樣本值) * Sigmoid*(1-Sigmoid) = -(輸出值-樣本值)*輸出值*(1-輸出值)
隱藏層→隱藏層:殘差 = (右層每個節點的殘差加權求和)* 當前節點的Sigmoid*(1-當前節點的Sigmoid)
如果用tansig作啟用函式,那麼:tansig導數 = 1 - tansig^2
殘差全部計算好後,就可以更新權重了:
輸入層:權重增加 = 當前節點的Sigmoid * 右層對應節點的殘差 * 學習率
隱藏層:權重增加 = 輸入值 * 右層對應節點的殘差 * 學習率
偏移值的權重增加 = 右層對應節點的殘差 * 學習率
學習率前面介紹過,學習率是一個預先設定好的引數,用於控制每次更新的幅度。
此後,對全部資料都反覆進行這樣的計算,直到輸出的誤差達到一個很小的值為止。
以上介紹的是目前最常見的神經網路型別,稱為前饋神經網路(FeedForward Neural Network),由於它一般是要向後傳遞誤差的,所以也叫BP神經網路(Back Propagation Neural Network)。
BP神經網路的特點和侷限:
- BP神經網路可以用作分類、聚類、預測等。需要有一定量的歷史資料,通過歷史資料的訓練,網路可以學習到資料中隱含的知識。在你的問題中,首先要找到某些問題的一些特徵,以及對應的評價資料,用這些資料來訓練神經網路。
- BP神經網路主要是在實踐的基礎上逐步完善起來的系統,並不完全是建立在仿生學上的。從這個角度講,實用性 > 生理相似性。
- BP神經網路中的某些演算法,例如如何選擇初始值、如何確定隱藏層的節點個數、使用何種啟用函式等問題,並沒有確鑿的理論依據,只有一些根據實踐經驗總結出的有效方法或經驗公式。
- BP神經網路雖然是一種非常有效的計算方法,但它也以計算超複雜、計算速度超慢、容易陷入區域性最優解等多項弱點著稱,因此人們提出了大量有效的改進方案,一些新的神經網路形式也層出不窮。
詳細的計算過程圖:








一般企業應用:
1.輸入輸出變數

2.演算法流程圖

To be continued(醫療輸入輸出變數的假想)