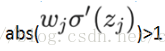1）梯度不穩定問題：

什麼是梯度不穩定問題：深度神經網路中的梯度不穩定性，前面層中的梯度或會消失，或會爆炸。

原因：前面層上的梯度是來自於後面層上梯度的乘乘積。當存在過多的層次時，就出現了內在本質上的不穩定場景，如梯度消失和梯度爆炸。

（2）梯度消失（vanishing gradient problem）：

原因：例如三個隱層、單神經元網路：

則可以得到：

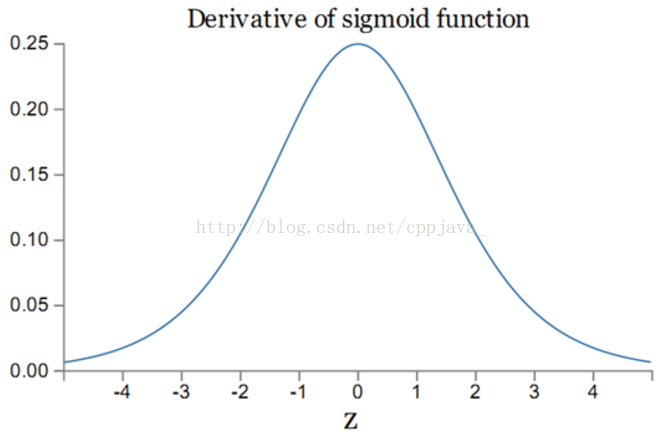
然而，sigmoid方程的導數曲線為：

可以看到，sigmoid導數的最大值為1/4，通常abs（w）<1,則：

前面的層比後面的層梯度變化更小，故變化更慢，從而引起了梯度消失問題。

（3）梯度爆炸（exploding gradient problem）：

當權值過大，前面層比後面層梯度變化更快，會引起梯度爆炸問題。

（4）sigmoid時，消失和爆炸哪個更易發生？

量化分析梯度爆炸出現時a的樹枝範圍：因為sigmoid導數最大為1/4，故只有當abs(w)>4時才可能出現

由此計算出a的數值變化範圍很小，僅僅在此窄範圍內會出現梯度爆炸問題。而最普遍發生的是梯度消失問題。

（5）如何解決梯度消失和梯度爆炸？

使用ReLU,maxout等替代sigmoid。（具體細節請看博主之前神經網路啟用函式部分）

區別：（1）sigmoid函式值在[0,1],ReLU函式值在[0,+無窮]，所以sigmoid函式可以描述概率，ReLU適合用來描述實數；（2）sigmoid函式的梯度隨著x的增大或減小和消失，而ReLU不會。

正因為有了這單側抑制，才使得神經網路中的神經元也具有了稀疏啟用性。尤其體現在深度神經網路模型(如CNN)中，當模型增加N層之後，理論上ReLU神經元的啟用率將降低2的N次方倍。這裡或許有童鞋會問：ReLU的函式影象為什麼一定要長這樣？反過來，或者朝下延伸行不行？其實還不一定要長這樣。只要能起到單側抑制的作用，無論是鏡面翻轉還是180度翻轉，最終神經元的輸出也只是相當於加上了一個常數項係數，並不影響模型的訓練結果。之所以這樣定，或許是為了契合生物學角度，便於我們理解吧。
那麼問題來了：這種稀疏性有何作用？換句話說，我們為什麼需要讓神經元稀疏？不妨舉栗子來說明。當看名偵探柯南的時候，我們可以根據故事情節進行思考和推理，這時用到的是我們的大腦左半球；而當看蒙面唱將時，我們可以跟著歌手一起哼唱，這時用到的則是我們的右半球。左半球側重理性思維，而右半球側重感性思維。也就是說，當我們在進行運算或者欣賞時，都會有一部分神經元處於啟用或是抑制狀態，可以說是各司其職。再比如，生病了去醫院看病，檢查報告裡面上百項指標，但跟病情相關的通常只有那麼幾個。與之類似，當訓練一個深度分類模型的時候，和目標相關的特徵往往也就那麼幾個，因此通過ReLU實現稀疏後的模型能夠更好地挖掘相關特徵，擬合訓練資料。

此外，相比於其它啟用函式來說，ReLU有以下優勢：對於線性函式而言，ReLU的表達能力更強，尤其體現在深度網路中；而對於非線性函式而言，ReLU由於非負區間的梯度為常數，因此不存在梯度消失問題(Vanishing Gradient Problem)，使得模型的收斂速度維持在一個穩定狀態。這裡稍微描述一下什麼是梯度消失問題：當梯度小於1時，預測值與真實值之間的誤差每傳播一層會衰減一次，如果在深層模型中使用sigmoid作為啟用函式，這種現象尤為明顯，將導致模型收斂停滯不前。