機器學習:神經網路-多層前饋神經網路淺析(附程式碼實現)
阿新 • • 發佈:2019-02-14
M-P神經元模型神經網路中最基本的組成成分:神經元模型。如下圖是一個典型的“M-P神經元模型”: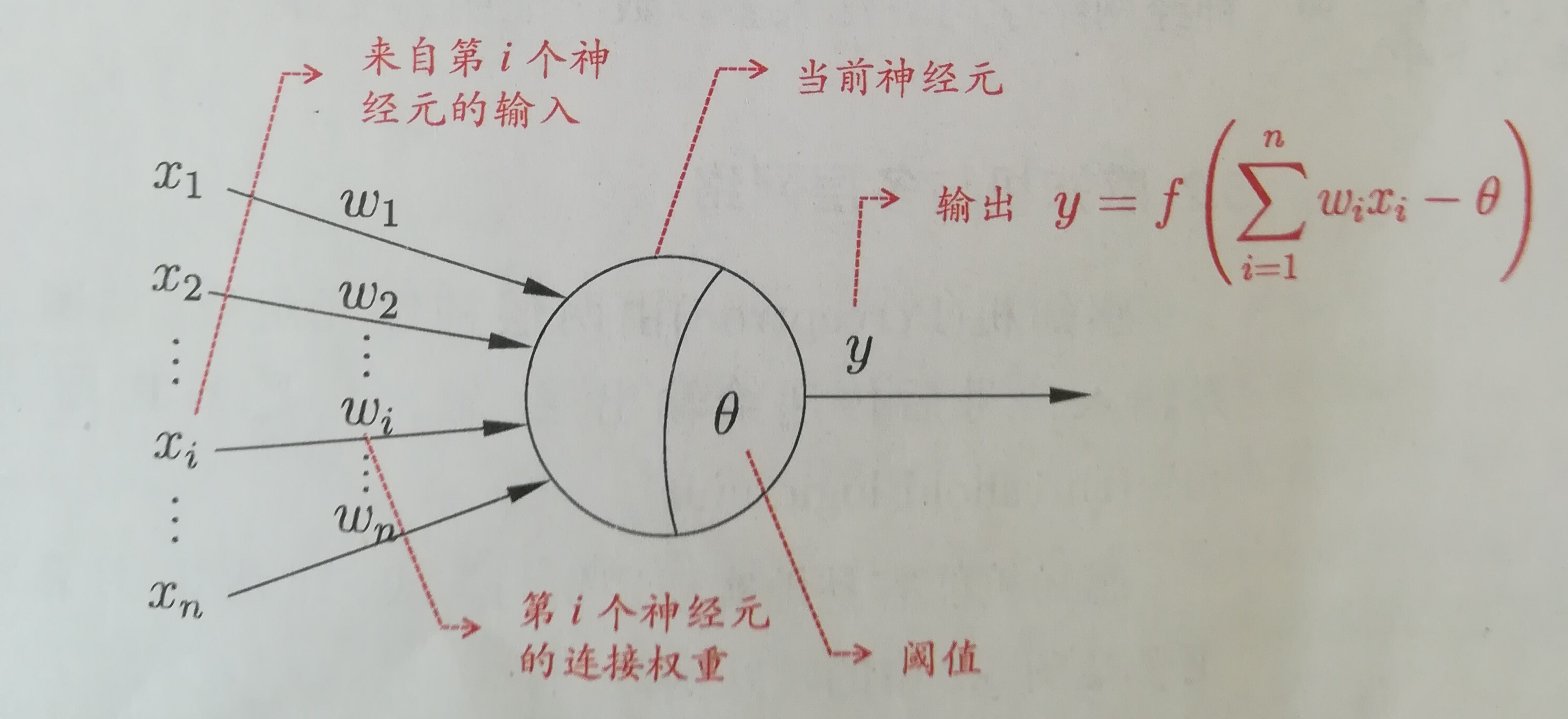 上圖中,神經元接收到n個其他神經元傳遞過來的輸入訊號,這些訊號通過權重的連線進行傳遞,神經元接收到的總輸入值與神經元的閾值進行比較,並通過“啟用函式”處理產生神經元輸出。常用S函式作為啟用函式:y=1/(1+e^-x);多層前饋神經網路定義:每層神經元與下一層神經元全互聯,不存在同層連線和跨層連線。包含一個輸入層,一個輸出層和若干個隱層。如下圖:
上圖中,神經元接收到n個其他神經元傳遞過來的輸入訊號,這些訊號通過權重的連線進行傳遞,神經元接收到的總輸入值與神經元的閾值進行比較,並通過“啟用函式”處理產生神經元輸出。常用S函式作為啟用函式:y=1/(1+e^-x);多層前饋神經網路定義:每層神經元與下一層神經元全互聯,不存在同層連線和跨層連線。包含一個輸入層,一個輸出層和若干個隱層。如下圖: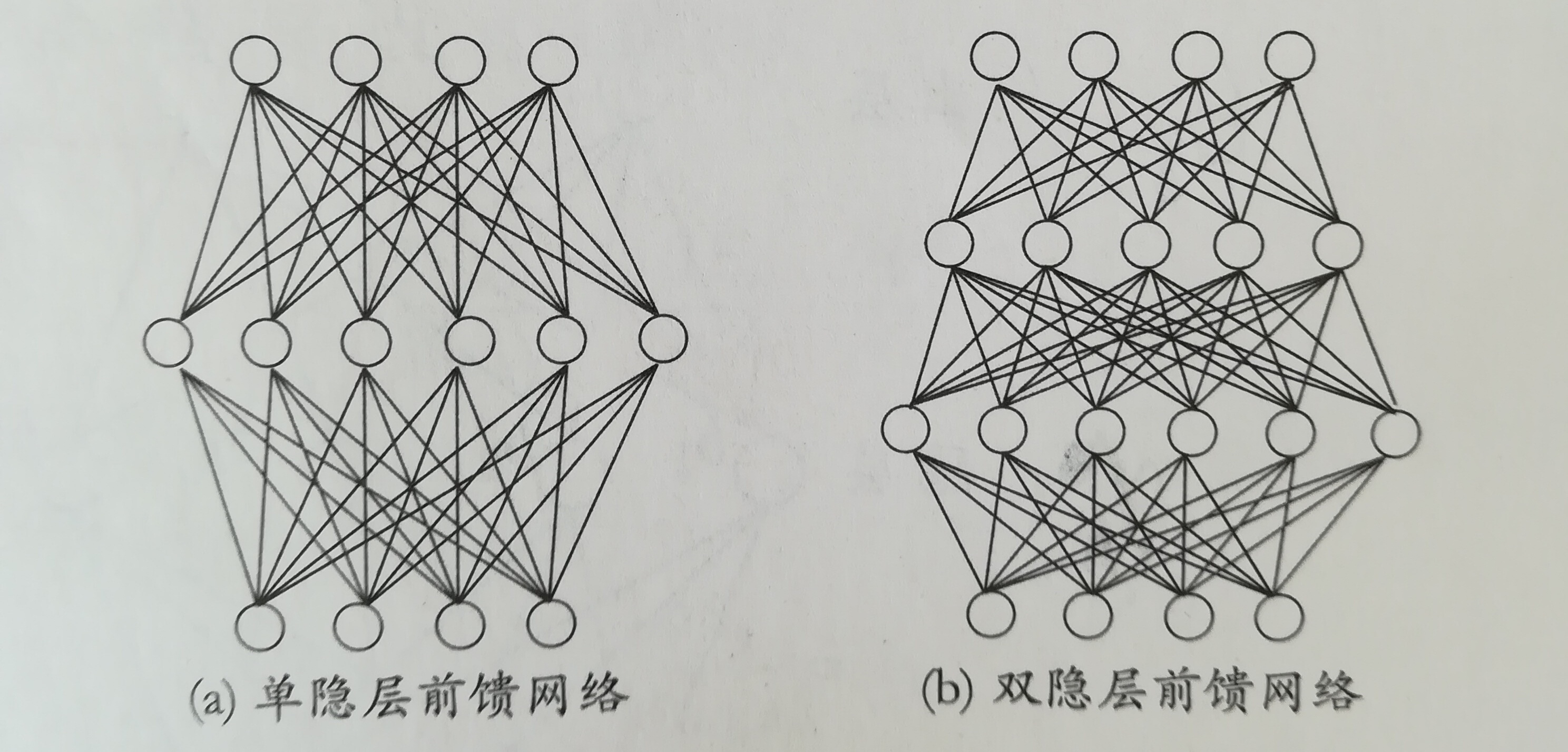 BP演算法(反向傳播演算法,誤差逆傳播演算法)
BP演算法(反向傳播演算法,誤差逆傳播演算法)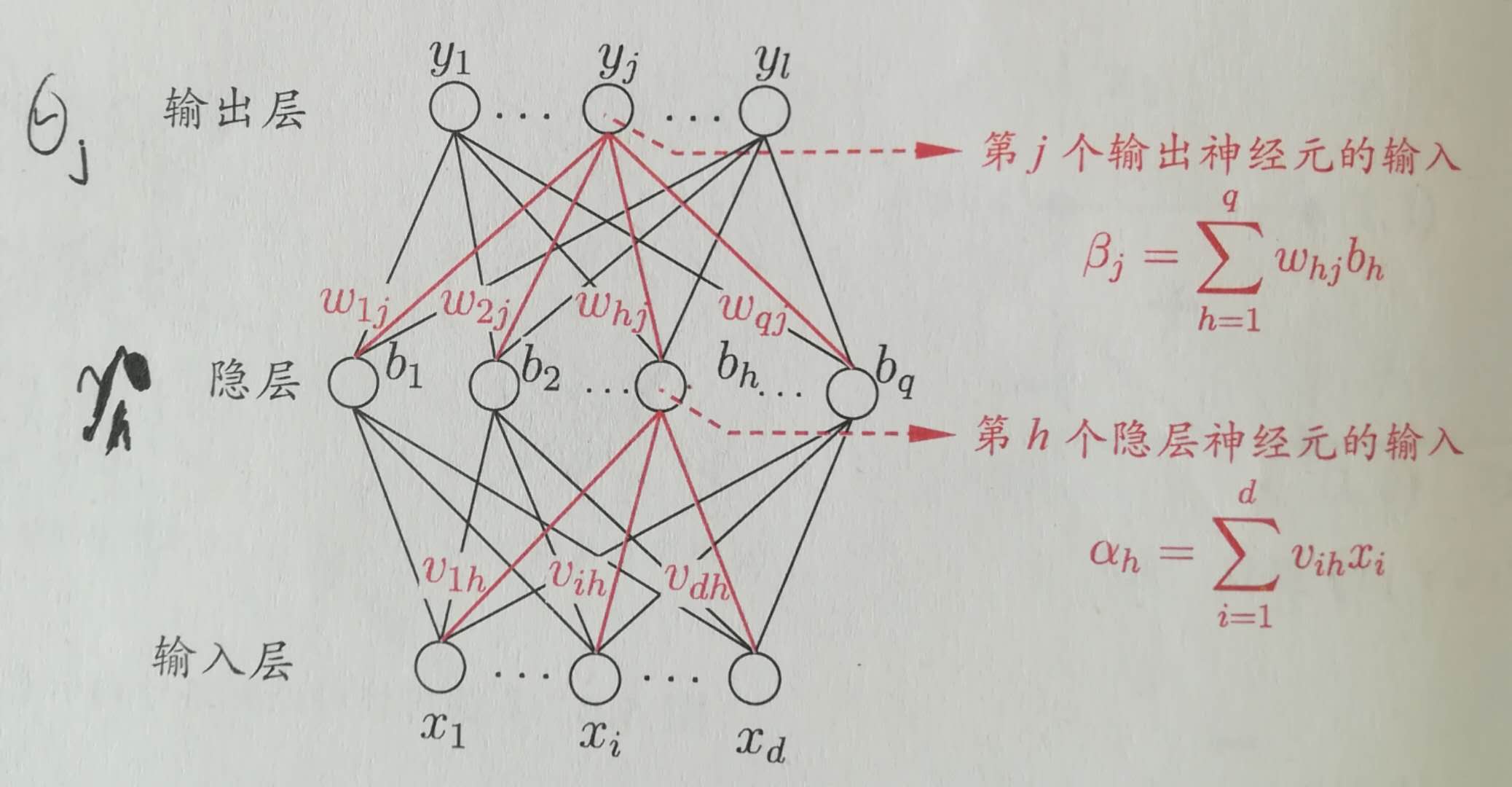 BP演算法推導:
BP演算法推導:
 BP演算法虛擬碼如下:
BP演算法虛擬碼如下:
 上圖中,神經元接收到n個其他神經元傳遞過來的輸入訊號,這些訊號通過權重的連線進行傳遞,神經元接收到的總輸入值與神經元的閾值進行比較,並通過“啟用函式”處理產生神經元輸出。常用S函式作為啟用函式:y=1/(1+e^-x);多層前饋神經網路定義:每層神經元與下一層神經元全互聯,不存在同層連線和跨層連線。包含一個輸入層,一個輸出層和若干個隱層。如下圖:
上圖中,神經元接收到n個其他神經元傳遞過來的輸入訊號,這些訊號通過權重的連線進行傳遞,神經元接收到的總輸入值與神經元的閾值進行比較,並通過“啟用函式”處理產生神經元輸出。常用S函式作為啟用函式:y=1/(1+e^-x);多層前饋神經網路定義:每層神經元與下一層神經元全互聯,不存在同層連線和跨層連線。包含一個輸入層,一個輸出層和若干個隱層。如下圖: BP演算法(反向傳播演算法,誤差逆傳播演算法)
BP演算法(反向傳播演算法,誤差逆傳播演算法) BP演算法推導:
BP演算法推導:
 BP演算法虛擬碼如下:
BP演算法虛擬碼如下:過擬合處理:1、將樣本分成訓練集和驗證集,當訓練集誤差降低但驗證集誤差升高,則停止訓練;2、正則化:誤差目標函式變為:E=lambda*(E1+E2+...+Em)/m+(1-lambda)(w1^2+w2^2+...+wi^2).
標準BP演算法和累積BP演算法matlab程式碼如下:if alg_type == 0,%標準BP演算法 for j=1:loops_num,%設定的梯度次數 for i=1:rows, %前向計算輸出 z1 = x_1(i,:)*w1_b; %隱層輸出 output1 = 1./(1+exp(-z1)); output1_b = [output1,1]; z2 = output1_b*w2_b; %輸出層輸出 output2 = 1./(1+exp(-z2)); %誤差 %error = (output2-y(i))*(output2-y(i))'; %反向傳播更新引數 g = (y(i)-output2).*output2.*(1-output2); %隱層與輸出層之間的權重變更 c_w2 = lambda2*output1'*g; %輸出層的閾值變更 c_b2 = -lambda2*g; c_w2_b = [c_w2;c_b2]; e = g*w2_b'(:,1:hidden_num).*output1.*(1-output1); %輸入層和隱層之間的權重變更 c_w1 = lambda1*x(i,:)'*e; %隱層的閾值變更 c_b1 = -lambda1*e; c_w1_b = [c_w1;c_b1]; %更新權重和閾值引數 w1_b = w1_b + c_w1_b; w2_b = w2_b + c_w2_b; endfor; %error endfor; else%累積BP演算法 for j=1:loops_num, c_w2 = zeros(hidden_num,2); c_b2 = zeros(1,2); c_w1 = zeros(cols-1,hidden_num); c_b1 = zeros(1,hidden_num); error = 0; %累積 for i=1:rows, z1 = x_1(i,:)*w1_b; output1 = 1./(1+exp(-z1)); output1_b = [output1,1]; z2 = output1_b*w2_b; output2 = 1./(1+exp(-z2)); g = (y(i)-output2).*output2.*(1-output2); c_w2 = c_w2 + lambda2*output1'*g; c_b2 = c_b2 - lambda2*g; e = g*w2_b'(:,1:hidden_num).*output1.*(1-output1); c_w1 = c_w1 + lambda1*x(i,:)'*e; c_b1 = c_b1 - lambda1*e; endfor; c_w2_b = [c_w2;c_b2]/rows; c_w1_b = [c_w1;c_b1]/rows; %累積更新 w1_b = w1_b + c_w1_b; w2_b = w2_b + c_w2_b; endfor; endif
參考資料:周志華《機器學習》

