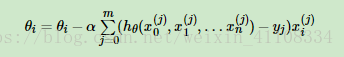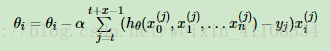機器學習:梯度下降gradient descent
視屏地址:https://www.bilibili.com/video/av10590361/?p=6
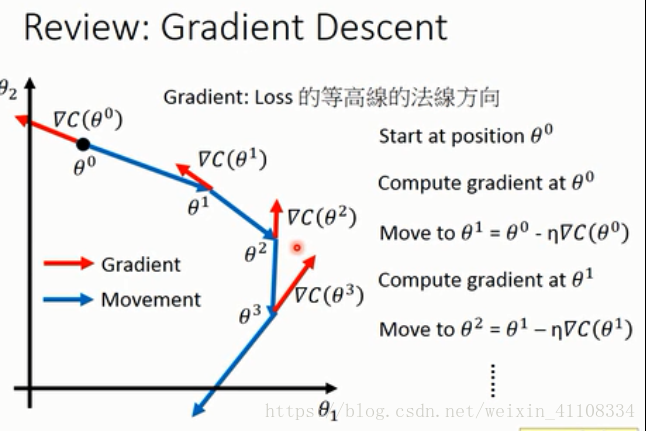
引數優化方法:梯度下降法 learning rate
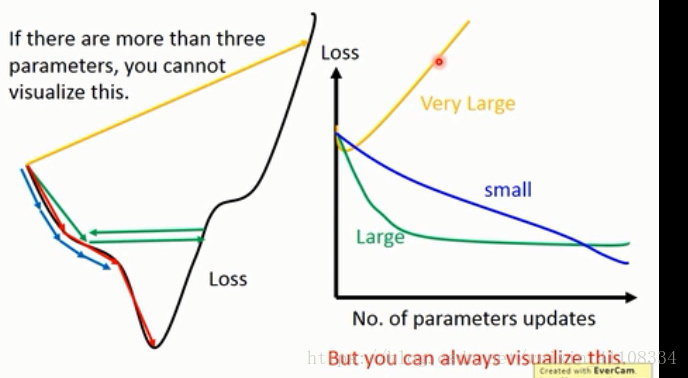
learning rate : 選擇rate大小
1、自動調learning rate ,隨著引數的epoch,rate 變小
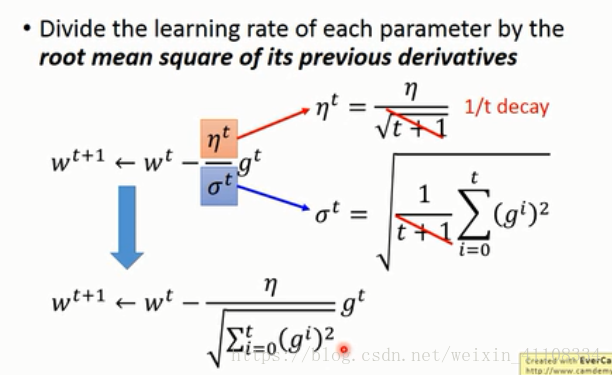
2、每一個引數都learning rate 都不一樣
Adagrad
例子:
造成反差效果
gradent desent:考慮全部的x的loss
stochastic gradent desent :隨機選擇一個x的loss
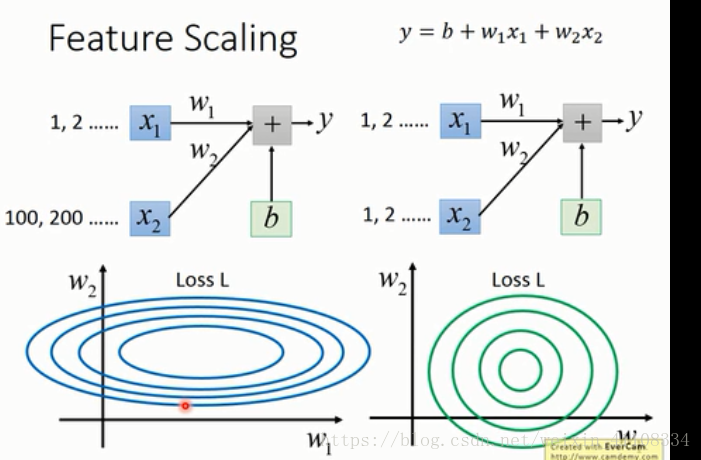
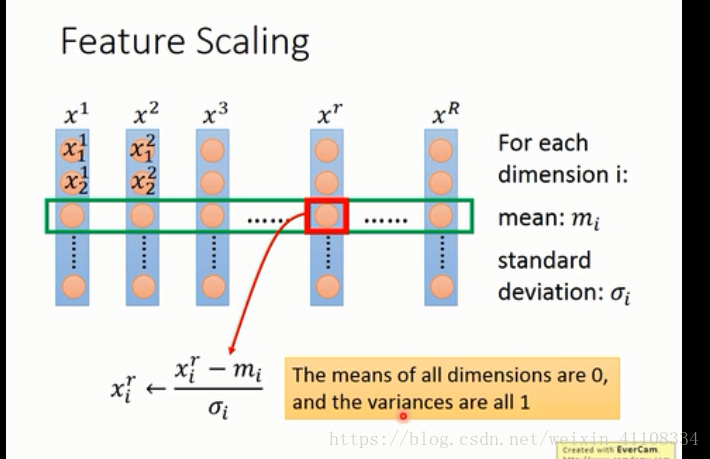
feature scaling :歸一化特徵縮放 調整x1 和x2的特徵的值,避免資料本身影響
歸一化 mormalization 標準化方法
標準化
https://www.cnblogs.com/pinard/p/5970503.html
在求解機器學習演算法的模型引數,即無約束優化問題時,在模型model,loss function 已知的情況下求解引數,優化方法。
梯度下降(Gradient Descent)是最常採用的方法之一,另一種常用的方法是最小二乘法。
1. 梯度
在微積分裡面,對多元函式的引數求∂偏導數,把求得的各個引數的偏導數以向量的形式寫出來,就是梯度。比如函式f(x,y), 分別對x,y求偏導數,求得的梯度向量就是(∂f/∂x, ∂f/∂y)T
那麼這個梯度向量求出來有什麼意義呢?他的意義從幾何意義上講,就是函式變化增加最快的地方。具體來說,對於函式f(x,y),在點(x0,y0),沿著梯度向量的方向就是(∂f/∂x0, ∂f/∂y0)T的方向是f(x,y)增加最快的地方。或者說,沿著梯度向量的方向,更加容易找到函式的最大值。反過來說,沿著梯度向量相反的方向,也就是 -(∂f/∂x0, ∂f/∂y0)T的方向,梯度減少最快,也就是更加容易找到函式的最小值。
2. 梯度下降與梯度上升
在機器學習演算法中,在最小化損失函式時,可以通過梯度下降法來一步步的迭代求解,得到最小化的損失函式,和模型引數值。反過來,如果我們需要求解損失函式的最大值,這時就需要用梯度上升法來迭代了。
梯度下降法和梯度上升法是可以互相轉化的。比如我們需要求解損失函式f(θ)的最小值,這時我們需要用梯度下降法來迭代求解。但是實際上,我們可以反過來求解損失函式 -f(θ)的最大值,這時梯度上升法就派上用場了。
3. 梯度下降法演算法詳解
3.1 梯度下降的直觀解釋
首先來看看梯度下降的一個直觀的解釋。比如我們在一座大山上的某處位置,由於我們不知道怎麼下山,於是決定走一步算一步,也就是在每走到一個位置的時候,求解當前位置的梯度,沿著梯度的負方向,也就是當前最陡峭的位置向下走一步,然後繼續求解當前位置梯度,向這一步所在位置沿著最陡峭最易下山的位置走一步。這樣一步步的走下去,一直走到覺得我們已經到了山腳。當然這樣走下去,有可能我們不能走到山腳,而是到了某一個區域性的山峰低處。
從上面的解釋可以看出,梯度下降不一定能夠找到全域性的最優解,有可能是一個區域性最優解。當然,如果損失函式是凸函式,梯度下降法得到的解就一定是全域性最優解。

3.2 梯度下降的相關概念
在詳細瞭解梯度下降的演算法之前,我們先看看相關的一些概念。

3.3 梯度下降的詳細演算法
梯度下降法的演算法可以有代數法和矩陣法(也稱向量法)兩種表示,如果對矩陣分析不熟悉,則代數法更加容易理解。不過矩陣法更加的簡潔,且由於使用了矩陣,實現邏輯更加的一目瞭然。這裡先介紹代數法,後介紹矩陣法。
3.3.1 梯度下降法的代數方式描述
3.3.2 梯度下降法的矩陣方式描述
這一部分主要講解梯度下降法的矩陣方式表述,相對於3.3.1的代數法,要求有一定的矩陣分析的基礎知識,尤其是矩陣求導的知識。
3.4 梯度下降的演算法調優
在使用梯度下降時,需要進行調優。哪些地方需要調優呢?
1. 演算法的步長選擇。Adagrad 或者 根據迭代次數 例如從0.1 到 0.001
在前面的演算法描述中,我提到取步長為1,但是實際上取值取決於資料樣本,可以多取一些值,從大到小,分別執行演算法,看看迭代效果,如果損失函式在變小,說明取值有效,否則要增大步長。前面說了。步長太大,會導致迭代過快,甚至有可能錯過最優解。步長太小,迭代速度太慢,很長時間演算法都不能結束。所以演算法的步長需要多次執行後才能得到一個較為優的值。
2. 演算法引數的初始值選擇。
初始值不同,獲得的最小值也有可能不同,因此梯度下降求得的只是區域性最小值;當然如果損失函式是凸函式則一定是最優解。由於有區域性最優解的風險,需要多次用不同初始值執行演算法,關鍵損失函式的最小值,選擇損失函式最小化的初值。
3.歸一化。
由於樣本不同特徵的取值範圍不一樣,可能導致迭代很慢,為了減少特徵取值的影響,可以對特徵資料歸一化,也就是對於每個特徵x,求出它的期望x¯和標準差std(x),然後轉化為:
這樣特徵的新期望為0,新方差為1,迭代次數可以大大加快。
4. 梯度下降法大家族(BGD,SGD,MBGD)
4.1 批量梯度下降法(Batch Gradient Descent) m個樣本
批量梯度下降法,是梯度下降法最常用的形式,具體做法也就是在更新引數時使用所有的樣本來進行更新,這個方法對應於前面3.3.1的線性迴歸的梯度下降演算法,也就是說3.3.1的梯度下降演算法就是批量梯度下降法。
由於我們有m個樣本,這裡求梯度的時候就用了所有m個樣本的梯度資料。
4.2 隨機梯度下降法(Stochastic Gradient Descent) 1個樣本
隨機梯度下降法,其實和批量梯度下降法原理類似,區別在與求梯度時沒有用所有的m個樣本的資料,而是僅僅選取一個樣本j來求梯度。對應的更新公式是:
隨機梯度下降法,和4.1的批量梯度下降法是兩個極端,一個採用所有資料來梯度下降,一個用一個樣本來梯度下降。自然各自的優缺點都非常突出。對於訓練速度來說,隨機梯度下降法由於每次僅僅採用一個樣本來迭代,訓練速度很快,而批量梯度下降法在樣本量很大的時候,訓練速度不能讓人滿意。對於準確度來說,隨機梯度下降法用於僅僅用一個樣本決定梯度方向,導致解很有可能不是最優。對於收斂速度來說,由於隨機梯度下降法一次迭代一個樣本,導致迭代方向變化很大,不能很快的收斂到區域性最優解。
那麼,有沒有一箇中庸的辦法能夠結合兩種方法的優點呢?有!這就是4.3的小批量梯度下降法。
4.3 小批量梯度下降法(Mini-batch Gradient Descent)1~m 之間x 值
小批量梯度下降法是批量梯度下降法和隨機梯度下降法的折衷,也就是對於m個樣本,我們採用x個樣子來迭代,1<x<m。一般可以取x=10,當然根據樣本的資料,可以調整這個x的值。對應的更新公式是:
5. 梯度下降法和其他無約束優化演算法的比較
在機器學習中的無約束優化演算法,除了梯度下降以外,還有前面提到的最小二乘法,此外還有牛頓法和擬牛頓法。
梯度下降法和最小二乘法相比,梯度下降法需要選擇步長,而最小二乘法不需要。梯度下降法是迭代求解,最小二乘法是計算解析解。如果樣本量不算很大,且存在解析解,最小二乘法比起梯度下降法要有優勢,計算速度很快。但是如果樣本量很大,用最小二乘法由於需要求一個超級大的逆矩陣,這時就很難或者很慢才能求解解析解了,使用迭代的梯度下降法比較有優勢。
梯度下降法和牛頓法/擬牛頓法相比,兩者都是迭代求解,不過梯度下降法是梯度求解,而牛頓法/擬牛頓法是用二階的海森矩陣的逆矩陣或偽逆矩陣求解。相對而言,使用牛頓法/擬牛頓法收斂更快。但是每次迭代的時間比梯度下降法長。