一、模糊系統

模糊控制系統分類

1 按訊號的時變特性分類

（1）恆值模糊控制系統

     系統的指令訊號為恆定值，通過模糊控制器消除外界對系統的擾動作用，使系統的輸出跟蹤輸入的恆定值。也稱為“自鎮定模糊控制系統”，如溫度模糊控制系統。

（2）隨動模糊控制系統

    系統的指令訊號為時間函式，要求系統的輸出高精度、快速地跟蹤系統輸入。也稱為“模糊控制跟蹤系統”或“模糊控制伺服系統”。

3 按靜態誤差是否存分類

（1）有差模糊控制系統

    將偏差的大小及其偏差變化率作為系統的輸入為有差模糊控制系統。

（2）無差模糊控制系統

    引入積分作用，使系統的靜差降至最小。

4 按系統控制輸入變數的多少分類

        控制輸入個數為1的系統為單變數模糊控制系統，控制輸入個數>1的系統為多變數模糊控制系統。

二、模糊控制器

在確定性控制系統中，根據控制器輸出的個數，可分為單變數控制系統和多變數控制系統。在模糊控制系統中也可類似地劃分為單變數模糊控制和多變數模糊控制。

1、單變數模糊控制器

在單變數模糊控制器（Single Variable Fuzzy Controller—SVFC）中，將其輸入變數的個數定義為模糊控制的維數。

（1）一維模糊控制器  如圖4-5(a)所示，一維模糊控制器的輸入變數往往選擇為受控量和輸入給定的偏差量E。由於僅僅採用偏差值，很難反映過程的動態特性品質，因此，所能獲得的系統動態效能是不能令人滿意的。這種一維模糊控制器往往被用於一階被控物件。

（2）二維模糊控制器   如圖4-5(b)所示，二維模糊控制器的兩個輸入變數基本上都選用受控變數和輸入給定的偏差E和偏差變化EC，由於它們能夠較嚴格地反映受控過程中輸出變數的動態特性，因此，在控制效果上要比一維控制器好得多，也是目前採用較廣泛的一類模糊控制器。

（3）三維模糊控制器  如圖4-5(c)

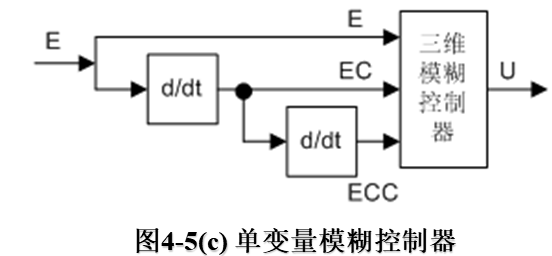
模糊控制系統所選用的模糊控制器維數越高，系統的控制精度也就越高。但是維數選擇太高，模糊控制規律就過於複雜，這是人們在設計模糊控制系統時，多數採用二維控制器的原因。

2、多變數模糊控制器

一個多變數模糊控制器（Multiple Variable Fuzzy Controller）系統所採用的模糊控制器，具有多變數結構，稱之為多變數模糊控制器。如圖4-6所示。

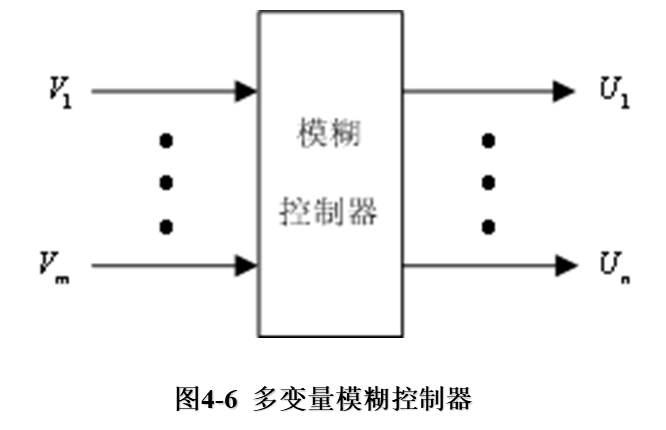
要直接設計一個多變數模糊控制器是相當困難的，可利用模糊控制器本身的解耦特點，通過模糊關係方程求解，在控制器結構上實現解耦，即將一個多輸入-多輸出（MIMO）的模糊控制器，分解成若干個多輸入-單輸出（MISO）的模糊控制器，這樣可採用單變數模糊控制器方法設計。

三、模糊控制器的設計

模糊控制器的設計步驟

模糊控制器最簡單的實現方法是將一系列模糊控制規則離線轉化為一個查詢表（又稱為控制表）。這種模糊控制其結構簡單，使用方便，是最基本的一種形式。

1、模糊控制器的結構

   單變數二維模糊控制器是最常見的結構形式。

2、定義輸入輸出模糊集

    對誤差E、誤差變化EC及控制量u的模糊集及其論域定義如下：

E、EC和u的模糊集均為：{NB,NM,NS,ZO,PS,PM,PB}

E、EC的論域均為：{-3，-2，-1，0，1，2，3}

u的論域為：{-4.5,-3,-1.5,0,1,3,4.5}

3、 定義輸入輸出隸屬函式

       模糊變數誤差E、誤差變化EC及控制量u的模糊集和論域確定後，需對模糊語言變數確定隸屬函式，確定論域內元素對模糊語言變數的隸屬度。

4 、建立模糊控制規則

      根據人的經驗，根據系統輸出的誤差及誤差的變化趨勢來設計模糊控制規則。模糊控制規則語句構成了描述眾多被控過程的模糊模型。

5、 建立模糊控制表

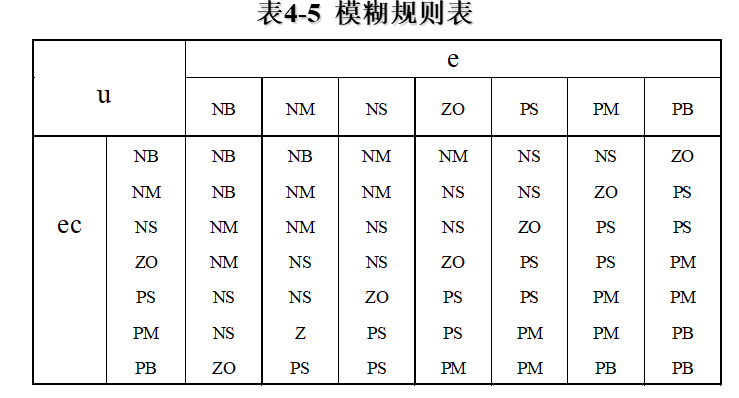
        模糊控制規則可採用模糊規則表4-5來描述，共49條模糊規則，各個模糊語句之間是或的關係，由第一條語句所確定的控制規則可以計算出u₁。同理，可以由其餘各條語句分別求出控制量u₂,…,u₄₉，則控制量為模糊集合U可表示為 ：

6 模糊推理

    模糊推理是模糊控制的核心，它利用某種模糊推理演算法和模糊規則進行推理，得出最終的控制量。

7 反模糊化

    通過模糊推理得到的結果是一個模糊集合。但在實際模糊控制中，必須要有一個確定值才能控制或驅動執行機構。將模糊推理結果轉化為精確值的過程稱為反模糊化。常用的反模糊化有三種：

(1)最大隸屬度法

   選取推理結果模糊集合中隸屬度最大的元素作為輸出值，即：

如果在輸出論域V中，其最大隸屬度對應的輸出值多於一個，則取所有具有最大隸屬度輸出的平均值，即：

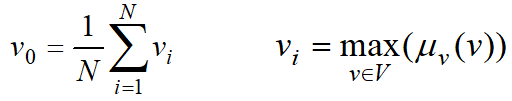
N為具有相同最大隸屬度輸出的總數。

最大隸屬度法不考慮輸出隸屬度函式的形狀，只考慮最大隸屬度處的輸出值。因此，難免會丟失許多資訊。它的突出優點是計算簡單。在一些控制要求不高的場合，可採用最大隸屬度法。

(2) 重心法

       為了獲得準確的控制量，就要求模糊方法能夠很好的表達輸出隸屬度函式的計算結果。重心法是取隸屬度函式曲線與橫座標圍成面積的重心為模糊推理的最終輸出值，即：

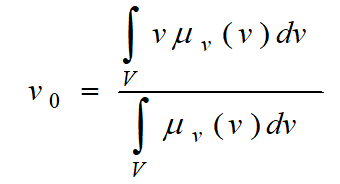
對於具有m個輸出量化級數的離散域情況：

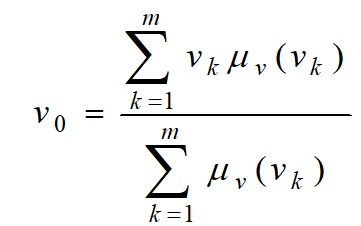
與最大隸屬度法相比較，重心法具有更平滑的輸出推理控制。即使對應於輸入訊號的微小變化，輸出也會發生變化。

(3)加權平均法

    工業控制中廣泛使用的反模糊方法為加權平均法，輸出值由下式決定：

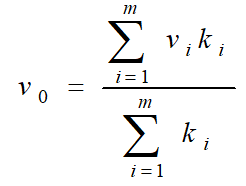
其中係數k_i的選擇根據實際情況而定。不同的係數決定系統具有不同的響應特性。當係數k_i取隸屬度μ_v(v_i)時，就轉化為重心法。

反模糊化方法的選擇與隸屬度函式形狀的選擇、推理方法的選擇相關

        Matlab提供五種解模糊化方法：（1）centroid：面積重心法；（2）bisector：面積等分法；（3）mom：最大隸屬度平均法；（4）som最大隸屬度取小法；（5）lom：大隸屬度取大法；

   在Matlab中，可通過setfis()設定解模糊化方法，通過defuzz()執行反模糊化運算。