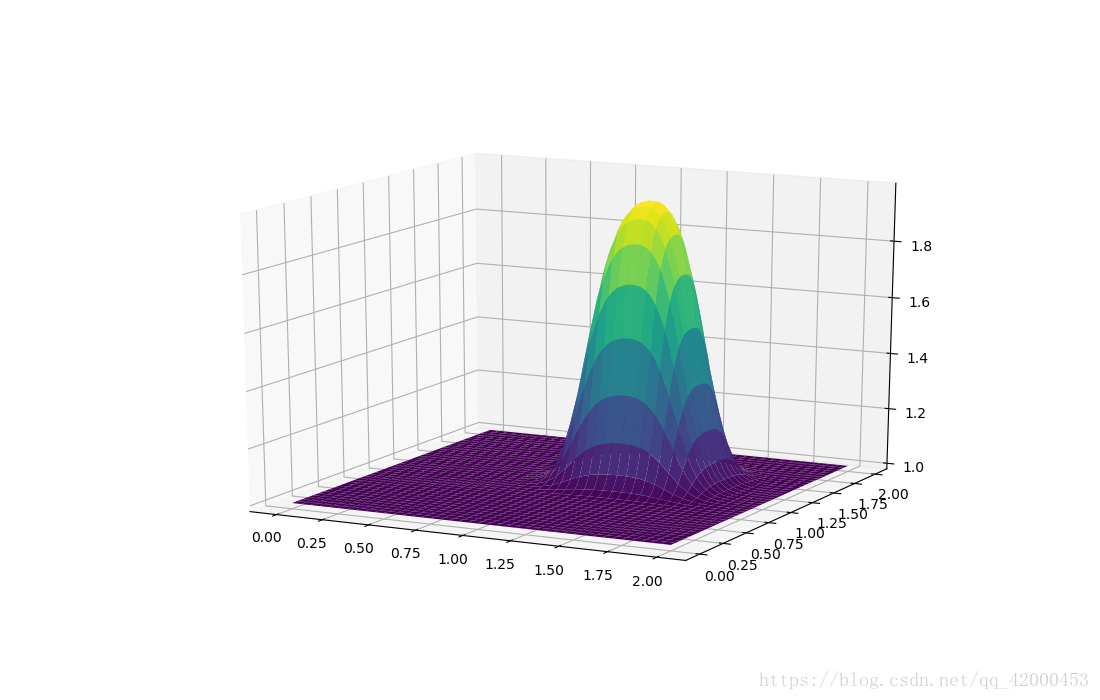
對二維線性對流方程的學習——來自流沙公眾號
阿新 • • 發佈:2018-11-16
許久沒接觸python,又有點忘了
繼續學習流沙公眾號
對這個方程,非定常項,以及x和y方向的對流項
碰巧今天看安德魯的計算流體力學偏微分方程所講,利用克萊姆法則和特徵值法來判斷方程的屬性
例子為一階,在做習題碰到二階。
此為閒話
同時,根據文章所寫,稍加修改,將for迴圈和陣列放在同一程式中進行對比,以溫習python,發現遺忘甚多。
from mpl_toolkits.mplot3d import Axes3D # 新 import numpy as np import matplotlib.pyplot as plt import time nx = 81 ny = 81 nt = 100 # 時間步 c = 1 # 常數 dx = 2 / (nx - 1) dy = 2 / (ny - 1) sigma = 0.2 dt = sigma * dx x = np.linspace(0,2,nx) y = np.linspace(0,2,ny) u = np.ones((ny,nx)) un = np.ones((ny,nx)) u[int(0.5/dy):int(1/dy+1),int(0.5/dx):int(1/dx+1)] = 2 print("forloop? matrix?") choose = input() # 對比for迴圈運算和陣列運算的速度 if choose == 'forloop': # for 迴圈 start = time.perf_counter() for n in range(nt + 1): ## loop across number of time steps un = u.copy() row, col = u.shape for j in range(1,row): for i in range(1, col): u[j, i] = (un[j,i] - (c * dt / dx * (un[j, i] - un[j, i - 1])) - (c * dt / dy * (un[j, i] - un[j - 1, i]))) u[0, :] = 1 u[-1, :] = 1 u[:, 0] = 1 u[:, -1] = 1 end = time.perf_counter() else: # 陣列運算 start = time.perf_counter() for n in range(nt + 1): ## matrix un = u.copy() u[1:, 1:] = (un[1:, 1:] - (c * dt / dx * (un[1:, 1:] - un[1:, :-1])) - (c * dt / dy * (un[1:, 1:] - un[:-1, 1:]))) u[0, :] = 1 u[-1, :] = 1 u[:, 0] = 1 u[:, -1] = 1 end = time.perf_counter() time_elapsed = end - start # 普通計算耗時 print("time: %f" %(time_elapsed)) fig = plt.figure(figsize=(11, 7), dpi=100) ax = Axes3D(fig) # 說明此圖為3D x,y = np.meshgrid(x,y) surf2 = ax.plot_surface(x, y, u[:],cmap = 'viridis') # cmap 表示的名字 plt.show()
對於此程式程式碼的說明:
1、from mpl_toolkits.mplot3d import Axes3D ,是3維繪圖的庫ax = Axes3D(fig)
2、放棄time.clock(),改為time.perf_counter()計時
結果
陣列計算的時間為0.0206
for迴圈的計算時間為3.604