bfs演算法，寬度優先搜尋演算法。

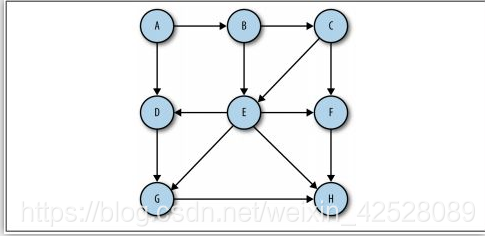
def bfs(graph,start):
     queue,visited = [start],[start]
     while queue:
            vertex=queue.pop()
            for i in graph[vertex]:
                    if i not in visited:
                          visited.append(i)
                          queue.append(i)
     return visited

G={"A":{"B","D"},
    "B":{"C","E"},
    "C":{"E","F"},
    "D":{"G"},
    "E":{"D","F","G","H"},
    "F":{"H"},
    "G":{"H"},
    "H":{}}
print(bfs(G,'A'  ))
 

【'A', 'B', 'D', 'E', 'C', 'G', 'H', 'F'】

DFS演算法：深度優先搜尋演算法

def dfs(graph,vertex,queue=[]):
        queue.append(vertex)
        for i in graph[vertex]:
               if i not in queue:
                      queue=dfs(graph,i,queue)
        return queue
       
graph = { 1: [ 2, 3 ], 2: [ 4, 5 ],
                    3: [ 5 ], 4: [ 6 ], 5: [ 6 ],
                    6: [ 7 ], 7: [] }


print(dfs(graph,1,))


 

執行結果[1, 2, 3, 4, 5, 6, 7]

dijkstra 演算法：求訪問完所有節點的最短路徑

G = {1: {2: 5, 4: 2, 5: 7},
     2: {3: 4},
     3: {},
     4: {2: 1, 3: 10},
     5: {3: 3}}

def dijkstra(graph,source):
     visited =set()
     distance = dict((k ,float("inf")) for k in G.keys())
     distance[source]=0
     while len(G)!=len(visited):
          visited.add(source)
          for next_node in  graph[source]:
                 if distance[next_node]>distance[source]+graph[source][next_node]:
                          distance[next_node]=distance[source]+graph[source][next_node]
          INF=float("inf")
          for node in distance.keys():
                 if node not in visited and distance[node]< INF:
                         INF,source= distance[node],node
     return distance
distance = dijkstra(G, 1)
print(distance)
 

執行結果：

{1: 0, 2: 3, 3: 7, 4: 2, 5: 7}