輾轉相除法求模的逆元
最近研究RSA演算法,發現在這個演算法裡,實現過程中的核心就是求出金鑰D,求金鑰的公式:
E*D ≡ 1 mod r ,現在已知了E和r,求E即是一個求模的逆元問題。注:≡是數論中表示同餘的符號。公式中,≡符號的左邊必須和符號右邊同餘,也就是兩邊模運算結果相同。顯而易見,不管r取什麼值(r是N的尤拉函式值,N是大素數p與q的乘積),符號右邊1 mod r 的結果都等於1;符號的左邊d與e的乘積做模運算後的結果也必須等於1,即滿足 (E*D)/mod r = 1 。
問題:
求A關於模N的逆元B,即要找出整數B,使A * B mod N = 1 (或A * B = x * N + 1),這裡要求A與N互素。
方法:
輾轉相除法(歐幾里德演算法)
-該演算法原用於求兩個數的最大公約數,經過變形可用於求模逆元
首先對餘數進行輾轉相除:
N = A * a0 + r0
A = r0 * a1 + r1
r0 = r1 * a2 + r2
r1 = r2 * a3 + r3
…
rn-2 = rn-1 * an + rn
rn-1 = rn * an+1 + 0
對上面的商數逆向排列(不含餘數為0的商數):

其中:
b-1 = 1
b0 = an
bi = an-1 * bi-1 + bi-2
如果n為奇數(即商個數為偶數),則bn即為所求的逆元B;
如果n為偶數(即商個數為奇數),則N-bn
實踐一下
求61關於模105的逆。先對餘數輾轉相除:
105 = 61 * 1 + 44
61 = 44 * 1 + 17
44 = 17 * 2 + 10
17 = 10 * 1 + 7
10 = 7 * 1 + 3
7 = 3 * 2 + 1
3 = 1 * 3 + 0
將商數逆序排列:

由於商的個數為偶數,因此31即為61關於模105的逆元。(31 * 61 = 105 * 18 + 1)
求31關於模105的逆,先對餘數輾轉相除:
105 = 31 * 3 + 12
31 = 12 * 2 + 7
12 = 7 * 1 + 5
7 = 5 * 1 + 2
5 = 2 * 2 + 1
2 = 1 * 2 + 0
將商數逆序排列:
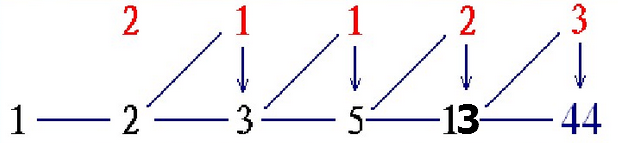
由於商的個數為奇數,因此105-44=61即為31關於105的逆元。
輾轉相除法求模逆元代的碼實現
輾轉相除法求判斷互質
/*****************************************************************************************************************
* 輾轉相除法, 又名歐幾里德演算法(Euclidean algorithm),是求最大公約數的一種方法。它的具體做法是:用較小數除較大數,
*再用出現的餘數(第一餘數)去除除數,再用出現的餘數(第二餘數)去除第一餘數,如此反覆,直到最後餘數是0為止。如果是
*求兩個數的最大公約數,那麼最後的除數就是這兩個數的最大公約數 ——百度百科
*****************************************************************************************************************/
//Python
//這段程式碼是使用輾轉相除法求最大公約數,判斷條件為:如果直到n=1才除盡,說明m、n互質,即最大公約數為1
#求最大公約數,若最大公約數是1,且m,n>1,m與n不等,則說明m,n互質
def comm_div(m, n): #m>n
temp = m % n
while(temp != 0):
m = n
n = temp
temp = m % n
if n == 1: #說明互質,返回True
return True
// C語言
#include <stdio.h>
#include <stdlib.h>
int pan_duan_hu_zhi(int* a, int* b)
{
int m,n,temp;
m = *a;
n = *b;
temp = m % n;
while(temp != 0)
{
m = n;
n = temp;
temp = m % n;
}
return n;
}
int main()
{
int a, b;
int Flag = 0;
//char ch,*arr,wei='a';
printf("請輸入a、b值,用空格間隔開\n");
scanf("%d%d", &a, &b); //從鍵盤獲取a、b值
// 資料整理保證 m > n
if(a<b)
{
Flag = a;
a = b;
b = Flag;
Flag = 0;
}
Flag = pan_duan_hu_zhi(&a, &b);
if(Flag == 1)
printf("%d和%d互質\n",a,b);
else
printf("%d和%d的最大公約數為%d",a,b,Flag);
getchar();
return 0;
}
輾轉相除法求模的逆
//Python 程式碼
#用輾轉相除法求質數e關於尤拉公式F的逆元
def _e_product(e, F):
a_list = []
m = F
n = e
temp = m % n
while (temp != 0):
a = (m - temp) / n
a_list.append(a)
m = n
n = temp
temp = m % n
print("a_list:", a_list)
a_list.reverse() #逆序
print("a_list_reverse:", a_list)
b_list = []
b_list.append(1)
b_list.append(a_list[0])
print("(最初插入的兩個1及a_list[0])b_list:", b_list)
for i in range(len(a_list)-1):
b = b_list[-1] * a_list[i+1] + b_list[-2]
b_list.append(b)
print("b_list", b_list)
#a_list存放的是商數,如果商數個數是偶數 b_list[-1]即為所求逆元
#若為奇數,F-b_list[-1]為所求的逆元
if len(a_list) % 2 == 0: #偶數
return b_list[-1]
else:
return F - b_list[-1]
// C程式碼
// 程式碼寫得比較爛,列印資訊也不去了,多多包涵>_<
#include <stdio.h>
#include <stdlib.h>
#include <memory.h>//要使用memset是要包含此標頭檔案
int _E_Product (int* e, int* F)
{
int i, a, m, n, temp,j,k,D,f;
int *p_quotient, *q_remainer, *p_quotient_reverse, *b_list;
p_quotient = (int*)malloc(512*(sizeof(int*))); // 存放每輪計算得到的商
q_remainer = (int*)malloc(512*(sizeof(int*))); // 存放每輪計算得到的餘數
p_quotient_reverse = (int*)malloc(512*(sizeof(int*))); // 存放逆序排列後的商
b_list = (int*)malloc(512*(sizeof(int*))); // 存放bn的陣列
memset(p_quotient,0,512); // 擦淨記憶體
memset(q_remainer,0,512);
memset(p_quotient_reverse,0,512);
memset(b_list,0,512);
f = *F; // 儲存F值,以備後續使用
m = *F;
n = *e;
temp = m % n;
printf("m = %d; n = %d; temp = %d \n",m,n,temp);
i = 0;
while(temp != 0)
{
q_remainer[i] = temp;
a = (m-temp)/n;
p_quotient[i] = a;
i++;
m = n;
n = temp;
temp = m % n;
}
for(j=0;j<i;j++)
{
printf("第%d輪商為%d\n",(j+1),p_quotient[j]);
printf("第%d輪餘數為%d\n",(j+1),q_remainer[j]);
}
//商逆序排列
k = i-1;
for(j=0;j<i;j++)
{
p_quotient_reverse[j] = p_quotient[k--];
}
printf("逆序後的商序列為:\n");
for(j=0;j<i;j++)
{
printf("%d\n",p_quotient_reverse[j]);
}
//計算bn
//插入最初的b0 = 1,及b1 = an 即 b1 = p_quotient_reverse[0]
b_list[0] = 1;
b_list[1] = p_quotient_reverse[0];
printf("b_list[%d]為:%d\n",1,b_list[1]);
//迭代計算
for(j=0;p_quotient_reverse[j+1] != 0;j++)
{
b_list[j+2] = b_list[j+1] * p_quotient_reverse[j+1] + b_list[j];
printf("b_list[%d]為:%d\n",(j+2),b_list[j+2]);
}
printf("b_list完整序列值:\n");
for(j=0;j<i+1;j++)
{
printf("%d\n",b_list[j]);
}
// 判斷商的個數決定金鑰為bn(偶數個)還是 F-bn(奇數個)
if(i%2 == 0)
{
printf("偶數\n");
printf("%d\n",j-1);
printf("%d\n",b_list[j-1]);
D = b_list[j-1];
}
else
{
printf("奇數\n");
printf("%d\n",j-1);
printf("%d\n",b_list[j-1]);
printf("%d\n",f);
D = f - b_list[j-1];
}
free(p_quotient);
free(q_remainer);
free(p_quotient_reverse);
printf("%d\n",D);
printf("返回金鑰...\n");
return D;
}
int main()
{
int p, q, e, d, n, fai_n;
printf("請輸入p、q、e值,用空格間隔開\n");
scanf("%d%d%d", &p, &q, &e); //從鍵盤獲取p、q、e值
n = p*q;
printf("N = %d\n",n);
fai_n = (p-1)*(q-1); //Φ(n)
printf("φ(n) = %d\n",fai_n);
getchar();
printf("計算金鑰...\n");
d = _E_Product(&e,&fai_n);
printf("金鑰計算完成...\n");
printf("金鑰D = %d\n",d);
getchar();
}
後記
由維基百科描述:
計算e對於φ(n)的模反元素d,所謂"模反元素"就是指有一個整數d,可以使得ed被φ(n)除的餘數為1。
ed ≡ 1 (mod φ(n))
這個式子等價於
ed - 1 = kφ(n)
那麼選定e後,是否可以利用湊數法去湊出來等式:ed - 1 = kφ(n) 的解?找到k,即
for k from 0 increase,judge [(kφ(n) + 1) % e ] == 0 是否成立,當它成立的時候,就找到了k,然後通過
(kφ(n)+1)% e 得到模逆元d,這個與通過輾轉相除法求模逆元好理解的多。
但是對於選定了e之後,等式ed - 1 = kφ(n) 的k解是否是唯一的? 若是不是唯一的,這個方法就出現了漏洞,他僅僅是找到第一個使式子成立的k就結束了。但是反過來講,若k不唯一,那麼d也將是不唯一的,這樣會出現對於一個公鑰e,私鑰d是不唯一的???雖然我沒有仔細去研究RSA演算法的證明,但我覺得對於一個既定公鑰e,與之對應的私鑰d必定要是唯一的~~~歡迎補充證明 >_<
n = p*q;
fai_n = (p-1)*(q-1); //Φ(n)
for (k = 0; (k*fai_n + 1) % e != 0; k++);
if ((k*fai_n + 1) % e == 0)
d = (k*fai_n + 1) / e;
算數基本定理:任何大於1的整數都可以分解成素數乘積的形式,並且,如果不計分解式中素數的次序,該分解式是唯一的[微軟中國1]。
由算數基本定理可知,整數分解為素數乘積的形式唯一,那麼可以不用使用輾轉相除法求金鑰D了!!!
