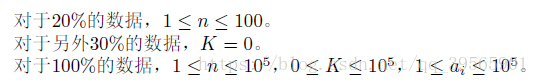JZOJ 4307. 【NOIP2015模擬11.3晚】喝喝喝
阿新 • • 發佈:2018-11-17
JZOJ 4307. 【NOIP2015模擬11.3晚】喝喝喝
題目
Description
Input
Output
Sample Input
3 2
5 3 1
Sample Output
4
Data Constraint
題解
首先看一條顯而易見的性質,若滿足
,則
,且
。
為了求答案方便,每次迴圈到
時,加上以
結尾的滿足條件子陣列的個數。
怎麼求?
我們不難發現,假設當前以
結尾的滿足條件子陣列的開頭最小可到
,則以
結尾的滿足條件子陣列的開頭最小隻能到
,否則其中必包含“壞對”。
則我們設一個指標
,表示當前滿足條件子陣列的開頭最小為
,
是滿足遞增的。
考慮如何將
後移。
找到
前最後一個
滿足
是一個壞對,也就是
。
設
,表示
,且沒有滿足條件的更小的
,也就是最後一個滿足
的
。
更新
時,判斷
與
的大小關係,取較大值。
更新
陣列時,用
的時間,將所有的
(
)。
又有一個問題,
也是一個“壞對”,也就是
,但用這種方法判斷不出。
所以再用一個變數維護最後一個出現
的位置。
程式碼
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
int f[100010],a[100010];
int main()
{
int n,k,i,j,last=0,p=0;
long long ans=0;
scanf("%d%d",&n,&k);
for(i=1;i<=n;i++) scanf("%d",&a[i]);
for(i=1;i<=n;i++)
{
if(a[i]>k&&f[a[i]]>last) last=f[a[i]];
if(a[i]>k&&p>last) last=p;
ans+=i-last;
int t=a[i]-k;
if(a[i]==k) p=i;
for(j=1;j<=floor(sqrt(t));j++) if(t%j==0) f[j]=f[t/j]=i;
}
printf("%lld",ans);
return 0;
}