---

一、題目：換錢的最小次數

  給定陣列arr,arr中所有的值都為正數且不重複。每個值代表一種面值的貨幣，每種面值的貨幣可以使用任意張，再給定一個整數aim代表要找的錢數，求組成aim的最少貨幣數。

  舉個例子
  arr[5,2,3] ,aim=20
 　　4張5元可以組成20,並且是最小的，所以返回4
  arr[5,2,3],aim=0。
  　　不用任何貨幣就可以組成0元，這裡返回0.
  arr[5,2,3],ami=4
  　　這裡無法組成返回-1

思路：時間和空間都為O（M*aim)【len(arr) = M 】

dp 矩陣為：大小為M*aim

dp[i][j]的含義是在可以任意使用arr[0…i]貨幣的情況下，組成j所需的最小張數，矩陣的每一行和每一列可以先確定，其他的位置dp[i][j] = min( dp[i-1][j] , dp[i][j-arr[i]]+1)。

dp的第一行表示：只用 5 來分別構成 0……20 最少要多少張，比如 5 需要 1張，10需要2張，……構不成的賦系統最大值，最後返回-1。

dp的第二行表示：只用5和2分別構成0到20 最少要多少張。

dp的第三行表示：只用5，2，3分別構成0到20最少要多少張。

 

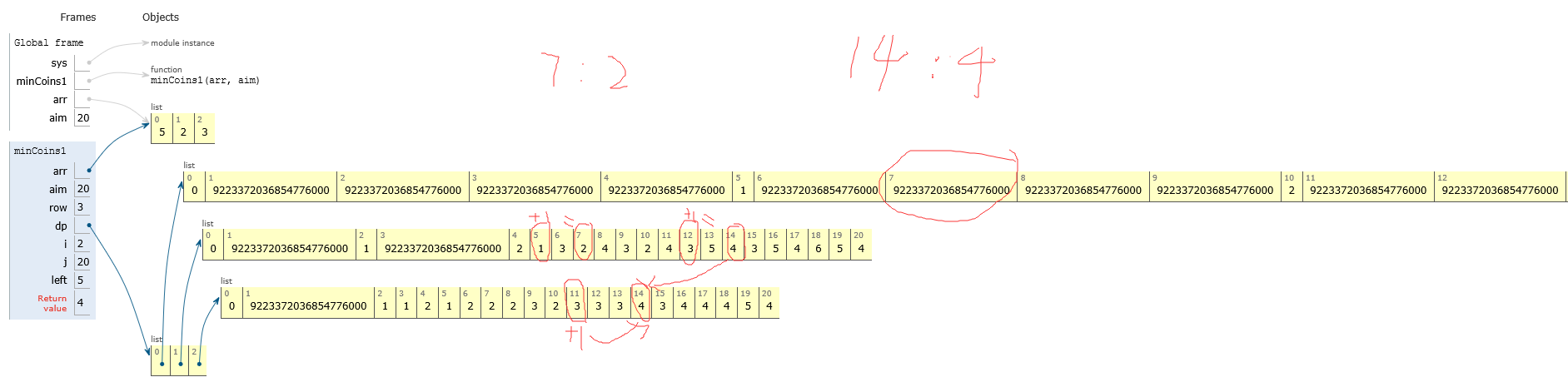
dp矩陣的構建：初始化系統最大值

• 第一列都為0，因為0不需要任何幣來構成。
• 第一行：能被5整除的賦值，值為整除的數。比如：5賦值1，10賦值2，15賦值3，20賦值4。
• 第二行、第三行……：

1. 比如：dp 第2行第7列的值 2 是根據
2. dp [7-2] +1 = 1 +1 =2來的，即【7可以由1個5和1個2組成】，
3. 但是還要看第一行7列的值是不是更小，即 dp [i][j] = min( dp [j-arr[i]] +1，dp [i-1][j] ），dp [j-arr[i]] +1不能是系統最大值。

 程式碼1：

import sys
def minCoins1(arr, aim):
    if arr == None or
 
 len(arr) == 0 or aim < 0:
        return -1
    row = len(arr)
    dp = [[sys.maxsize for i in range(aim+1)] for j in range(row)]
    for i in range(row):
        dp[i][0] = 0
    for j in range(1, aim+1):
        if j % arr[0] == 0:
            dp[0][j] = j // arr[0]
    for i in range(1, row):
        for j in range(1, aim+1):
            left = sys.maxsize
            if j - arr[i] >= 0 and dp[i][j-arr[i]] != sys.maxsize:
                left = dp[i][j-arr[i]] + 1
            dp[i][j] = min(left, dp[i-1][j])
    return dp[row-1][aim] if dp[row-1][aim] != sys.maxsize else -1
arr = [5,2,3]
aim = 20
minCoins1(arr, aim)

 程式碼2：時間為O（M*aim)【len(arr) = M 】，空間為O（aim+1)，dp 大小為 aim+1的列表

#經過空間壓縮的動態規劃
def minCoins2(arr, aim):
    if arr == None or len(arr) == 0 or aim < 0:
        return -1
    row = len(arr)
    dp = [sys.maxsize for i in range(aim+1)]
    dp[0] = 0
    for i in range(1, aim+1):
        if i % arr[0] == 0:
            dp[i] = i // arr[0]
    for i in range(1, row):
        dp[0] = 0
        for j in range(1, aim+1):
            left = sys.maxsize
            if j - arr[i] >= 0 and dp[j-arr[i]] != sys.maxsize:
                left = dp[j-arr[i]] + 1
            dp[j] = min(left, dp[j])
    return dp[aim] if dp[aim] != sys.maxsize else -1

 

---

題目二：換錢的方法數

https://blog.csdn.net/qq_34342154/article/details/77122125

給定陣列arr，arr中所有的值都為整數且不重複。每個值代表一種面值的貨幣，每種貨幣有無數張，再給定一個整數aim代表要找的錢數，求換錢的方法有多少種。

思路1：暴力遞迴，最壞情況下時間O(aim^N)，N表示陣列的長度

首先介紹暴力遞迴的方法。如果arr = [5, 10, 25, 1]，aim = 1000，分析過程如下：
用０張５元的貨幣，讓[10, 25, 1]組成剩下的1000，最終方法數記為res1。
用１張５元的貨幣，讓[10, 25, 1]組成剩下的995，最終方法數記為res2。
用２張５元的貨幣，讓[10, 25, 1]組成剩下的990，最終方法數記為res3。
……
用201張５元的貨幣，讓[10, 25, 1]組成剩下的0，最終方法數記為res201。
那麼res1 + res2 + res3 + …… +res201的值就是中的方法數。

 

#暴力遞迴方法
def coins1(arr, aim):
    def process1(arr, index, aim):
        if index == len(arr):
            return 1 if aim == 0 else 0
        else:
            res = 0
            for i in range(0, aim//arr[index]+1):
                res += process1(arr, index+1, aim-arr[index]*i)
        return res


    if arr == None or len(arr) == 0 or aim < 0:
        return 0
    return process1(arr, 0, aim)

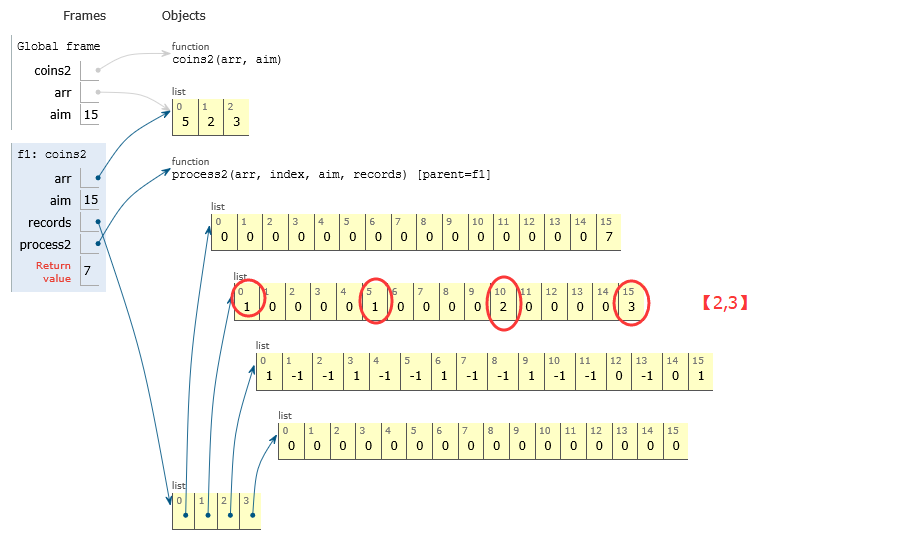
思路2：記憶搜尋：時間複雜度為O(N*aim^2)，空間複雜度O(N*aim)。

採用一個字典儲存計算過的結果，暴力遞迴會重複計算結果。比如使用0張5元+1張10元的情況和使用2張5元+0張10元的情況，都需要求[25, 1]組成剩下的990的方法數。記憶搜尋就是使用一張記錄表將遞迴過程中的結果進行記錄，當下次再遇到同樣的遞迴過程，就直接使用表中的資料。

 

第三行：圈出的

第一步：當0個5：當0個2，只用【3】構成15的方法：1個

　　　　　　　　　1個2，只用【3】構成13的方法：-1個【不可能】

　　　　　　　　　2個2，……

　　　　　　　　　……

　　　　　　　　　7個2……

第三行：圈出的

第二步：當1個5時，當0個2，只用【3】構成10：-1個

　　　　　　　　　    1個2，只用【3】構成8：-1個

　　　　　　　　　　……

　　　　　　　　　　5個2，只用【3】構成0：1個

第二行：

當0個5時：只用【2，3】構成15有3種方法

當1個5時：只用【2，3】構成10有2種方法

當2個5時：只用【2，3】構成5有1種方法

當3個5時：只用【2，3】構成0有1種方法

 

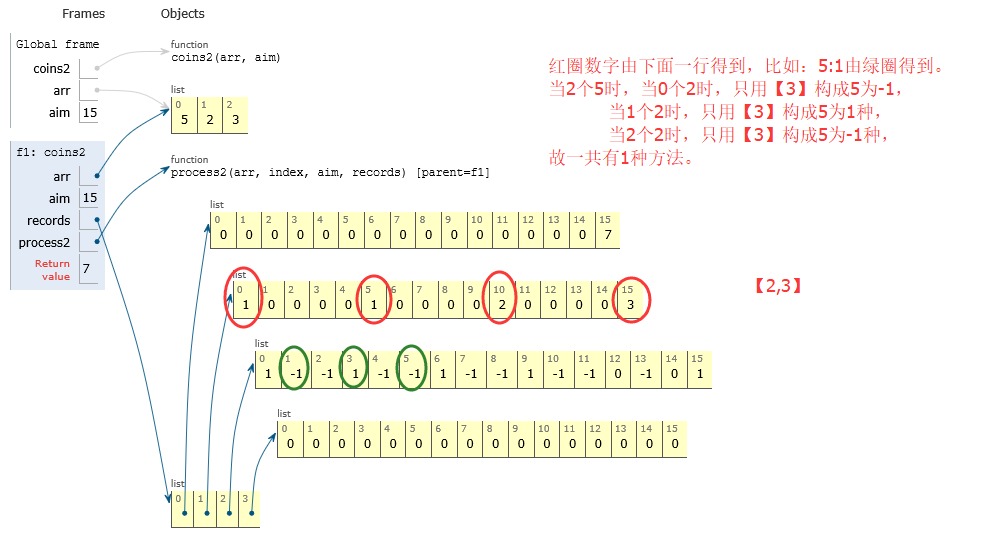
第一行：結果，用【5，2，3】構成15有7種方法

 程式碼：

def coins2(arr, aim):
    def process2(arr, index, aim, records):
        if index == len(arr):
            return 1 if aim == 0 else 0
        else:
            res = 0
            for i in range(0, aim//arr[index]+1):
                mapValue = records[index+1][aim-arr[index]*i]
                if mapValue != 0:
                    res += mapValue if mapValue != -1 else 0
                else:
                    res += process2(arr, index+1, aim-arr[index]*i, records)
        records[index][aim] = -1 if res == 0 else res
        return res


    if arr == None or len(arr) == 0 or aim < 0:
        return 0
    records = [[0 for i in range(aim+1)] for j in range(len(arr)+1)]
    return process2(arr, 0, aim, records)
arr = [5,2,3]
aim = 15
res1 = coins2(arr,aim)

 思路3：動態規劃：時間O（M*aim^2)，空間O（M*aim）

 

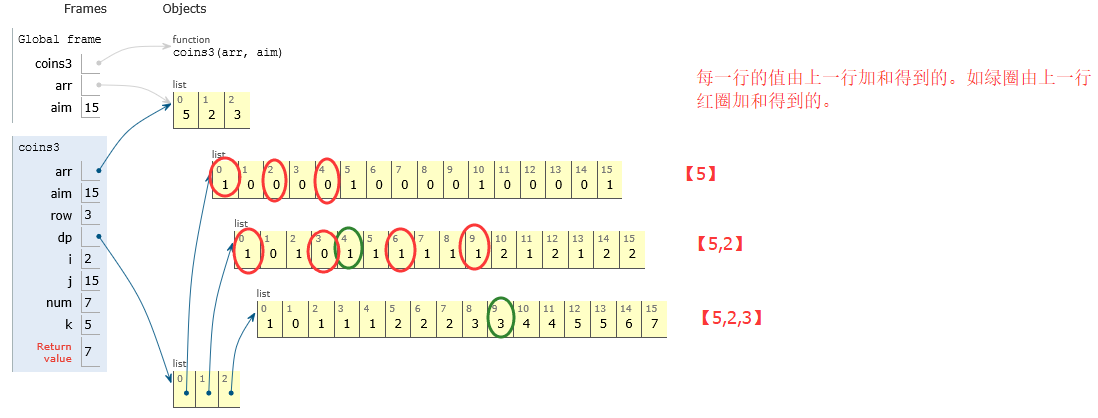
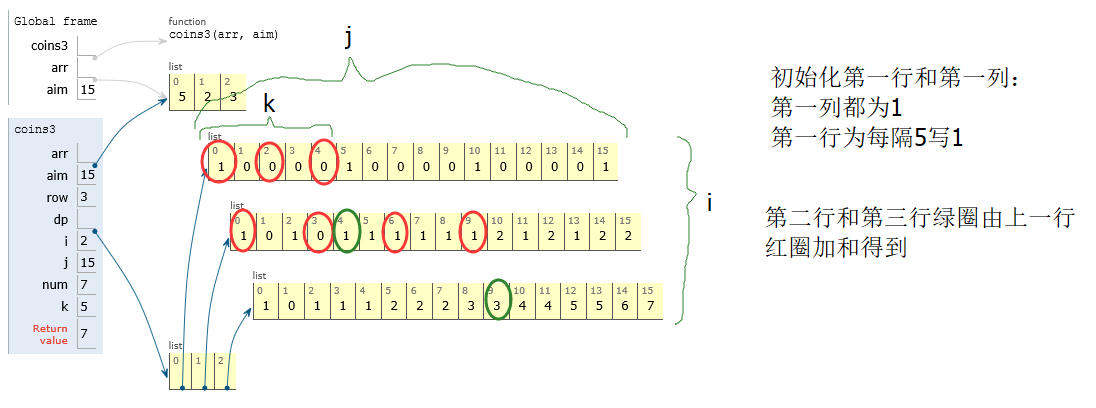
為何綠圈等於上一行紅圈的加和？即num += dp[i-1][j-arr[i]*k]

比如綠圈的第二行第5列那個1：只用【5，2】

上一行紅圈表示只用【5】構成0，2，4的方法數為1，0，0

則當用0個2時，對應【5】構成4方法數為0

當用1個2時，對應【5】構成2方法數為0

當2個2時，對應【5】構成0方法數為1

程式碼：

def coins3(arr, aim):
    if arr == None or len(arr) == 0 or aim < 0:
        return 0
    row = len(arr)
    dp = [[0 for i in range(aim+1)]for j in range(row)]
    for i in range(row):
        dp[i][0] = 1
    for j in range(1, aim//arr[0]+1):
        dp[0][arr[0]*j] = 1
    for i in range(1, row):
        for j in range(1, aim+1):
            num = 0
            for k in range(j//arr[i]+1):
                num += dp[i-1][j-arr[i]*k]
            dp[i][j] = num
    return dp[row-1][aim]

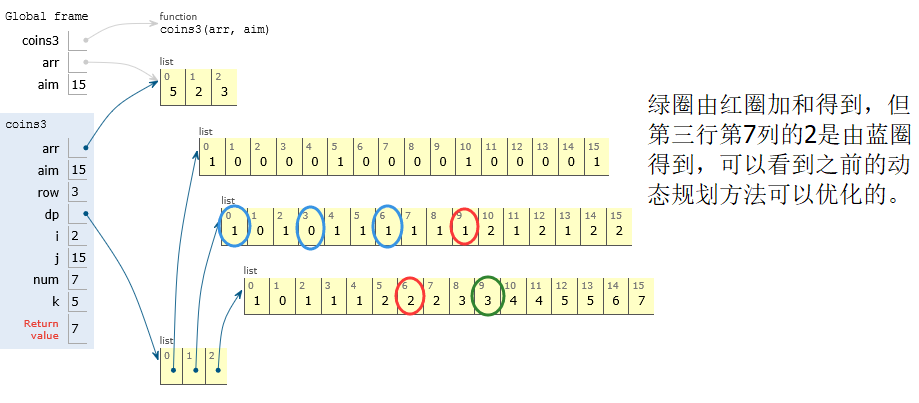
思路4：動態規劃時間的優化：時間O（M*aim)，空間O（M*aim）

思路3中的第三步迴圈k可省略。

for k in range(j//arr[i]+1):
          num += dp[i-1][j-arr[i]*k] 即

dp[i][j] = dp[i-1][j] + dp[i-1][j-arr[i]] + dp[i-1][j-2*arr[i]] + …dp[i-1][j-k*arr[i]]

等價於

dp[i][j] = dp[i-1][j] + dp[i][j-arr[i]]

程式碼：

def coins4(arr, aim):
    if arr == None or len(arr) == 0 or aim < 0:
        return 0
    row = len(arr)
    dp = [[0 for i in range(aim+1)] for j in range(row)]
    for i in range(row):
        dp[i][0] = 1
    for j in range(1, aim//arr[0]+1):
        dp[0][arr[0]*j] = 1
    for i in range(1,row):
        for j in range(1, aim+1):
            dp[i][j] = dp[i-1][j]
            dp[i][j] += dp[i][j-arr[i]] if j-arr[i] >= 0 else 0
    return dp[row-1][aim]

思路5：動態規劃空間的優化：時間O（M*aim)，空間O(aim)。

def coin5(arr,aim):
    if not arr or not aim:
        return 0
    dp = [0] * (aim + 1)
    for i in range(0,aim+1,arr[0]):
        dp[i] = 1
    for i in range(1,len(arr)):
        for j in range(1,aim+1):
            dp[j] += dp[j-arr[i]] if j - arr[i] >= 0 else 0
    return dp[-1]
arr = [5,2,3]
aim = 15
coin5(arr,aim)