字尾陣列 (Suffix Array) 學習筆記
\(\\\)
定義
介紹一些寫法和陣列的含義,首先要知道 字典序 。
- \(len\):字串長度
\(s\):字串陣列,我們的字串儲存在 \(s[0]...s[len-1]\) 中。
\(suffix(i) ,i\in[0,len-1]\): 表示子串 \(s[i]...s[len-1]\),即從 \(i\) 開始的字尾 。
加入我們提取出了 \(suffix(1)...suffix(len-1)\) ,將他們按照字典序從小到達排序。
- \(sa[i]\) :排名為 \(i\) 的字尾的第一個字元在原串裡的位置 。
- \(rank[i]\) :\(suffix(i)\)的排名。
顯然這兩個陣列可以在 \(O(N)\) 的時間內互相推出。
\(\\\)
Doubling Algorithm
由於博主太蒟並不會DC3,想看DC3的同志們可以溜了
\(\\\)
倍增構造法。
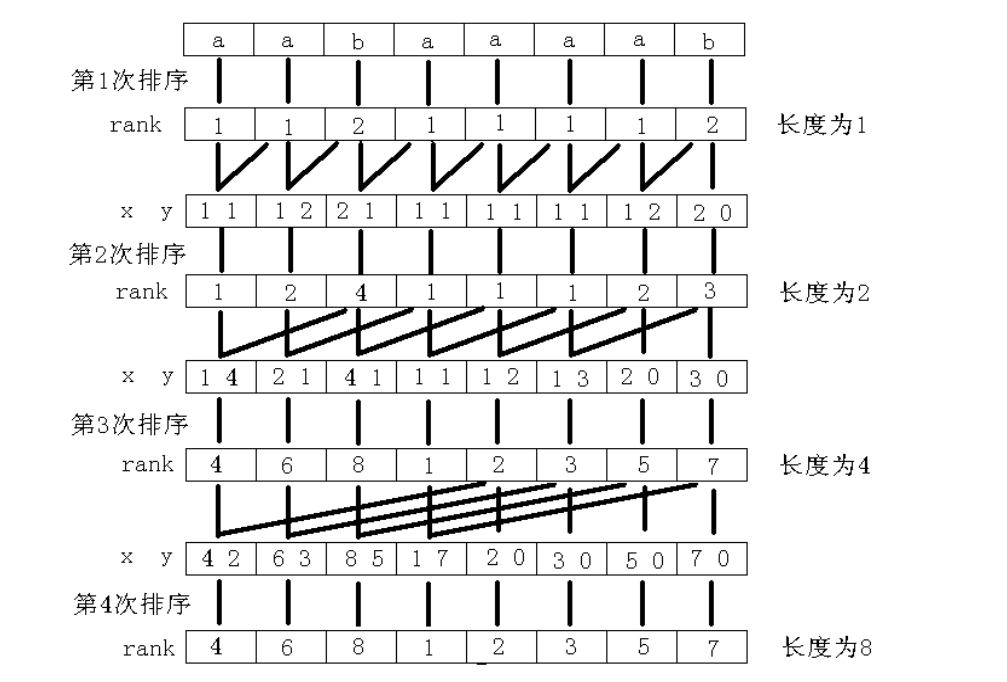
從小到大列舉 \(k\) ,每次按照字典序排序,每一個字尾的長度為 \(2^k\) 的字首,直到沒有相同排名的為止。
若有的字尾不夠長就在後面補上:比當前串全字符集最小字元還要小的字元,結果顯然符合字典序的定義。
\(\\\)
如何確定長度為 \(2^k\) 的每一個字尾對應字首的排名?
倍增。有點像數學歸納法的感覺。
首先我們顯然可以直接求出來 \(k=0\)
然後對於一個 \(k\) ,我們顯然已經完成了 \(k-1\) 部分的工作。
所以對於一個長度為 \(2^k\) 的字首,它顯然可以由兩個長度為 \(2^{k-1}\) 的字首拼成。
也就是說,我們可以把長度為 \(2^k\) 的字首,寫成兩個長度為 \(2^{k-1}\) 的字首的有序二元組。
有一個顯然的結論,因為長度 \(2^{k-1}\) 的所有字首有序,所以我們對這些二元組排序法則可以寫成:
以前一個長度為 \(2^{k-1}\) 的字首的 \(rank\) 為第一關鍵字,以後一個長度為 \(2^{k-1}\) 的字首的 \(rank\) 為第二關鍵字排序。
對於此方法得到的順序,與將整個長度為 \(2^k\)
附上 \(2009\) 年國家集訓隊論文中的排序圖片,可以加深體會一下整個排序的思想。
\(\\\)
