哈夫曼樹的介紹

Huffman Tree，中文名是哈夫曼樹或霍夫曼樹，它是最優二叉樹。

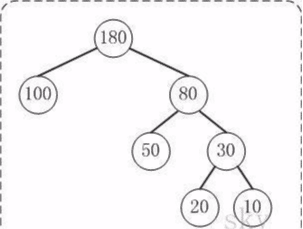
定義：給定n個權值作為n個葉子結點，構造一棵二叉樹，若樹的帶權路徑長度達到最小，則這棵樹被稱為哈夫曼樹。 這個定義裡面涉及到了幾個陌生的概念，下面就是一顆哈夫曼樹，我們來看圖解答。

(01) 路徑和路徑長度

 

定義：在一棵樹中，從一個結點往下可以達到的孩子或孫子結點之間的通路，稱為路徑。通路中分支的數目稱為路徑長度。若規定根結點的層數為1，則從根結點到第L層結點的路徑長度為L-1。

例子：100和80的路徑長度是1，50和30的路徑長度是2，20和10的路徑長度是3。

(02) 結點的權及帶權路徑長度

 

定義：若將樹中結點賦給一個有著某種含義的數值，則這個數值稱為該結點的權。結點的帶權路徑長度為：從根結點到該結點之間的路徑長度與該結點的權的乘積。

例子：節點20的路徑長度是3，它的帶權路徑長度= 路徑長度 * 權 = 3 * 20 = 60。

(03) 樹的帶權路徑長度

 

定義：樹的帶權路徑長度規定為所有葉子結點的帶權路徑長度之和，記為WPL。

例子：示例中，樹的WPL= 1*100 + 2*80 + 3*20 + 3*10 = 100 + 160 + 60 + 30 = 350。

比較下面兩棵樹

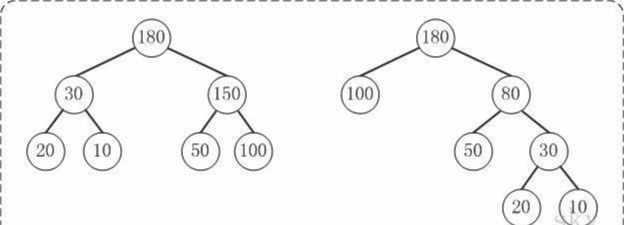
上面的兩棵樹都是以{10, 20, 50, 100}為葉子節點的樹。

 

左邊的樹WPL=2*10 + 2*20 + 2*50 + 2*100 = 360

右邊的樹WPL=350

左邊的樹WPL > 右邊的樹的WPL。你也可以計算除上面兩種示例之外的情況，但實際上右邊的樹就是{10,20,50,100}對應的哈夫曼樹。至此，應該堆哈夫曼樹的概念有了一定的瞭解了，下面看看如何去構造一棵哈夫曼樹。

哈夫曼樹的圖文解析

假設有n個權值，則構造出的哈夫曼樹有n個葉子結點。 n個權值分別設為 w1、w2、…、wn，哈夫曼樹的構造規則為：

 

1. 將w1、w2、…，wn看成是有n 棵樹的森林(每棵樹僅有一個結點)；

2. 在森林中選出根結點的權值最小的兩棵樹進行合併，作為一棵新樹的左、右子樹，且新樹的根結點權值為其左、右子樹根結點權值之和；

3. 從森林中刪除選取的兩棵樹，並將新樹加入森林；

4. 重複(02)、(03)步，直到森林中只剩一棵樹為止，該樹即為所求得的哈夫曼樹。

以{5,6,7,8,15}為例，來構造一棵哈夫曼樹。

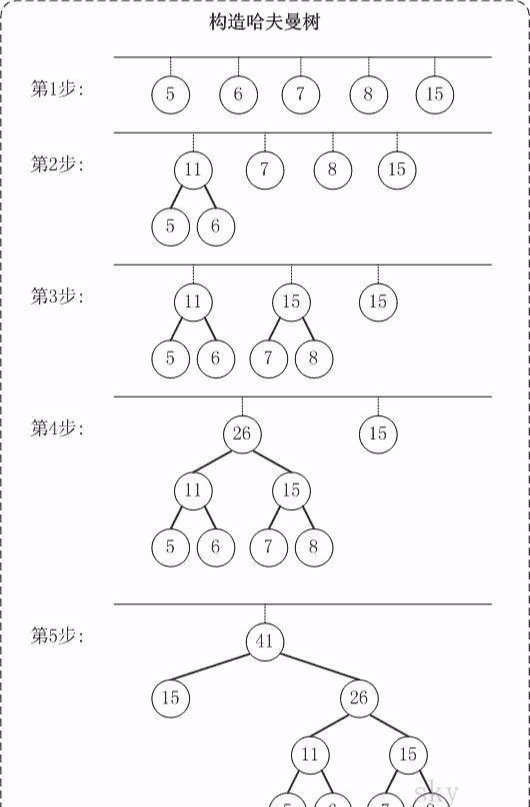
第1步：建立森林，森林包括5棵樹，這5棵樹的權值分別是5,6,7,8,15。

第2步：在森林中，選擇根節點權值最小的兩棵樹(5和6)來進行合併，將它們作為一顆新樹的左右孩子(誰左誰右無關緊要，這裡，我們選擇較小的作為左孩子)，並且新樹的權值是左右孩子的權值之和。即，新樹的權值是11。 然後，將"樹5"和"樹6"從森林中刪除，並將新的樹(樹11)新增到森林中。

第3步：在森林中，選擇根節點權值最小的兩棵樹(7和8)來進行合併。得到的新樹的權值是15。 然後，將"樹7"和"樹8"從森林中刪除，並將新的樹(樹15)新增到森林中。

第4步：在森林中，選擇根節點權值最小的兩棵樹(11和15)來進行合併。得到的新樹的權值是26。 然後，將"樹11"和"樹15"從森林中刪除，並將新的樹(樹26)新增到森林中。

第5步：在森林中，選擇根節點權值最小的兩棵樹(15和26)來進行合併。得到的新樹的權值是41。 然後，將"樹15"和"樹26"從森林中刪除，並將新的樹(樹41)新增到森林中。

此時，森林中只有一棵樹(樹41)。這棵樹就是我們需要的哈夫曼樹！

哈夫曼樹的基本操作

哈夫曼樹的重點是如何構造哈夫曼樹。本文構造哈夫曼時，用到了以前介紹過的"(二叉堆)最小堆"。下面對哈夫曼樹進行講解。

1. 基本定義

GIF

template <class T>class HuffmanNode{ public: T key; // 權值 HuffmanNode *left; // 左孩子 HuffmanNode *right; // 右孩子 HuffmanNode *parent;// 父結點 HuffmanNode(){} HuffmanNode(T value, HuffmanNode *l, HuffmanNode *r, HuffmanNode *p): key(value),left(l),right(r),parent(p) {}};

HuffmanNode是哈夫曼樹的節點類。

template <class T>class Huffman { private: HuffmanNode<T> *mRoot; // 根結點 public: Huffman(); ~Huffman(); // 前序遍歷"Huffman樹" void preOrder(); // 中序遍歷"Huffman樹" void inOrder(); // 後序遍歷"Huffman樹" void postOrder(); // 建立Huffman樹 void create(T a[], int size); // 銷燬Huffman樹 void destroy(); // 列印Huffman樹 void print(); private: // 前序遍歷"Huffman樹" void preOrder(HuffmanNode<T>* tree) const; // 中序遍歷"Huffman樹" void inOrder(HuffmanNode<T>* tree) const; // 後序遍歷"Huffman樹" void postOrder(HuffmanNode<T>* tree) const; // 銷燬Huffman樹 void destroy(HuffmanNode<T>* &tree); // 列印Huffman樹 void print(HuffmanNode<T>* tree, T key, int direction);};

Huffman是哈夫曼樹對應的類，它包含了哈夫曼樹的根節點和哈夫曼樹的相關操作。

2. 構造哈夫曼樹

/* * 建立Huffman樹 * * 引數說明： * a 權值陣列 * size 陣列大小 * * 返回值： * Huffman樹的根節點 */template <class T>void Huffman<T>::create(T a[], int size){ int i; HuffmanNode<T> *left, *right, *parent; MinHeap<T> *heap = new MinHeap<T>(); // 建立陣列a對應的最小堆 heap->create(a, size); for(i=0; i<size-1; i++) { left = heap->dumpFromMinimum(); // 最小節點是左孩子 right = heap->dumpFromMinimum(); // 其次才是右孩子 // 新建parent節點，左右孩子分別是left/right； // parent的大小是左右孩子之和 parent = new HuffmanNode<T>(left->key+right->key, left, right, NULL); left->parent = parent; right->parent = parent; // 將parent節點資料拷貝到"最小堆"中 if (heap->copyOf(parent)!=0) { cout << "插入失敗!" << endl << "結束程式" << endl; destroy(parent); parent = NULL; break; } } mRoot = parent; // 銷燬最小堆 heap->destroy(); delete heap;}

首先通過heap->create(a, size)來建立最小堆。最小堆構造完成之後，進入for迴圈。

每次迴圈時：

 

(01) 首先，將最小堆中的最小節點拷貝一份並賦值給left，然後重塑最小堆(將最小節點和後面的節點交換位置，接著將"交換位置後的最小節點"之前的全部元素重新構造成最小堆)；

(02) 接著，再將最小堆中的最小節點拷貝一份並將其賦值right，然後再次重塑最小堆；

(03) 然後，新建節點parent，並將它作為left和right的父節點；

(04) 接著，將parent的資料複製給最小堆中的指定節點。

在二叉堆中已經介紹過堆，這裡就不再對堆的程式碼進行說明了。