資料結構圖文解析之:哈夫曼樹與哈夫曼編碼詳解及C++模板實現
0. 資料結構圖文解析系列
1. 哈夫曼編碼簡介
哈夫曼編碼(Huffman Coding)是一種編碼方式,也稱為“赫夫曼編碼”,是David A. Huffman1952年發明的一種構建極小多餘編碼的方法。
在計算機資料處理中,霍夫曼編碼使用變長編碼表對源符號進行編碼,出現頻率較高的源符號採用較短的編碼,出現頻率較低的符號採用較長的編碼,使編碼之後的字串字串的平均長度 、期望值降低,以達到無失真壓縮資料的目的。
舉個例子,現在我們有一字串:
this is an example of a huffman tree
這串字串有36個字元,如果按普通方式儲存這串字串,每個字元佔據1個位元組,則共需要36 * 1 * 8 = 288bit。
經過分析我們發現,這串字串中各字母出現的頻率不同,如果我們能夠按如下編碼:
| 字母 | 頻率 | 編碼 | --- | 字母 | 頻率 | 編碼 |
|---|---|---|---|---|---|---|
| space | 7 | 111 | s | 2 | 1011 | |
| a | 4 | 010 | t | 2 | 0110 | |
| e | 4 | 000 | l | 1 | 11001 | |
| f | 3 | 1101 | o | 1 | 00110 | |
| h | 2 | 1010 | p | 1 | 10011 | |
| i | 2 | 1000 | r | 1 | 11000 | |
| m | 2 | 0111 | u | 1 | 00111 | |
| n | 2 | 0010 | x | 1 | 10010 |
編碼這串字串,只需要:
(7+4+4)x3 + (3+2+2+2+2+2+2)x4 + (1+1+1+1+1+1)x 5 = 45+60+30 = 135bit
編碼這串字串只需要135bit!單單這串字串,就壓縮了288-135 = 153bit。
那麼,我們如何獲取每個字串的編碼呢?這就需要哈夫曼樹了。
源字元編碼的長短取決於其出現的頻率,我們把源字元出現的頻率定義為該字元的權值。
2. 哈夫曼樹簡介
哈夫曼又稱最優二叉樹。是一種帶權路徑長度最短的二叉樹。它的定義如下。
哈夫曼樹的定義
假設有n個權值{w1,w2,w3,w4...,wn},構造一棵有n個節點的二叉樹,若樹的帶權路徑最小,則這顆樹稱作哈夫曼樹。這裡面涉及到幾個概念,我們由一棵哈夫曼樹來解釋
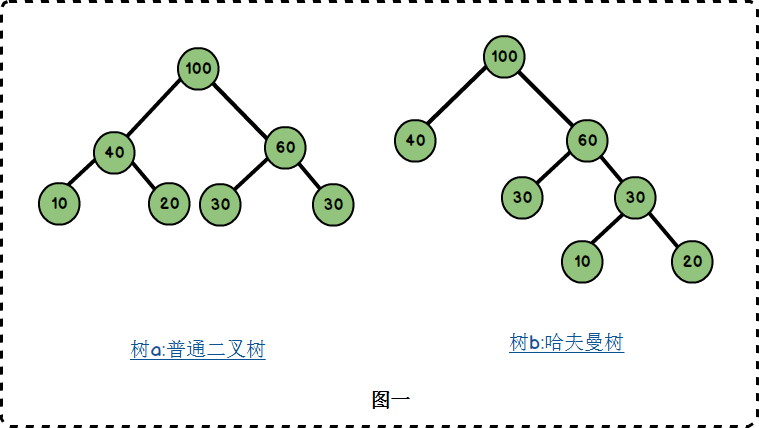
路徑與路徑長度:從樹中一個節點到另一個節點之間的分支構成了兩個節點之間的路徑,路徑上的分支數目稱作路徑長度。若規定根節點位於第一層,則根節點到第H層的節點的路徑長度為H-1.如樹b:100到60 的路徑長度為1;100到30的路徑長度為2;100到20的路徑長度為3。
- 樹的路徑長度:從根節點到每一節點的路徑長度之和。樹a的路徑長度為1+1+2+2+2+2 = 10;樹b的路徑長度為1+1+2+2+3+3 = 12.
- 節點的權:將樹中的節點賦予一個某種含義的數值作為該節點的權值,該值稱為節點的權;
- 帶權路徑長度:從根節點到某個節點之間的路徑長度與該節點的權的乘積。例如樹b中,節點10的路徑長度為3,它的帶權路徑長度為10 * 3 = 30;
樹的帶權路徑長度:樹的帶權路徑長度為所有葉子節點的帶權路徑長度之和,稱為WPL。樹a的WPL = 2*(10+20+30+40) = 200 ;樹b的WPL = 1x40+2x30+3x10+3x20 = 190.而哈夫曼樹就是樹的帶權路徑最小的二叉樹。
3. 構造哈夫曼樹
3.1 哈夫曼樹的節點結構
/*哈夫曼樹的節點定義*/
template <typename T>
struct HuffmanNode
{
HuffmanNode(T k,HuffmanNode<T>*l=nullptr,HuffmanNode<T>* r=nullptr)
:key(k),lchild(l), rchild(r){}
~HuffmanNode(){};
T key; //節點的權值
HuffmanNode<T>* lchild; //節點左孩
HuffmanNode<T>* rchild; //節點右孩
};- value: 節點的權值
- lchild:節點左孩子
- rchild:節點右孩子
3.2 哈夫曼樹的抽象資料型別
template <typename T>
class Huffman
{
public:
void preOrder(); //前序遍歷哈夫曼樹
void inOrder(); //中序遍歷哈夫曼樹
void postOrder(); //後序遍歷哈夫曼樹
void creat(T a[], int size); //建立哈夫曼樹
void destory(); //銷燬哈夫曼樹
void print(); //列印哈夫曼樹
Huffman();
~Huffman(){};
private:
void preOrder(HuffmanNode<T>* pnode);
void inOrder(HuffmanNode<T>* pnode);
void postOrder(HuffmanNode<T>*pnode);
void print(HuffmanNode<T>*pnode);
void destroy(HuffmanNode<T>*pnode);
private:
HuffmanNode<T>* root; //哈夫曼樹根節點
deque<HuffmanNode<T>*> forest;//森林
};- root:哈夫曼樹的根結點。
- forset : 森林,這裡使用deque來儲存森林中樹的根節點。
3.3 哈夫曼樹的構造步驟
假設有n個權值,則構造出的哈夫曼樹有n個葉子節點.n個權值記為{w1,w2,w3...wn},哈夫曼樹的構造過程為:
- 將w1,w2,w3...wn看成具有n棵樹的森林,每棵樹僅有一個節點。
- 從森林中,選取兩棵根節點權值最小的樹,兩棵樹分別作為左子樹與右子樹,構建一棵新樹。新樹的權值等於左右子樹權值之和。
- 從森林中刪除兩棵權值最小的樹,將構建完成後的新樹加入森林中。
- 重複2、3步驟,直到森林只剩一棵樹為止。這棵樹便是哈夫曼樹。
圖一的樹b為一棵哈夫曼樹,它的葉子節點為{10,20,30,40},以這4個權值構建樹b的過程為:

這個過程很編碼實現為:
/*建立哈夫曼樹*/
template<typename T>
void Huffman<T>::creat(T a[],int size)
{
for (int i = 0; i < size; i++) //每個節點都作為一個森林
{
//為初始序列的元素構建節點。每個節點作為一棵樹加入森林中。
HuffmanNode<T>* ptr = new HuffmanNode<T>(a[i],nullptr,nullptr);
forest.push_back(ptr);
}
for (int i = 0; i < size - 1; i++)
{
//排序,以選出根節點權值最小兩棵樹
sort(forest.begin(), forest.end(), [](HuffmanNode<T>* a, HuffmanNode<T>*b){return a->key< b->key; });
HuffmanNode<T>*node = new HuffmanNode<T>(forest[0]->key + forest[1]->key, forest[0], forest[1]); //構建新節點
forest.push_back(node); //新節點加入森林中
forest.pop_front(); //刪除兩棵權值最小的樹
forest.pop_front();
}
root = forest.front();
forest.clear();
};- 這裡僅僅示範構建哈夫曼樹的過程,沒有經過效能上的優化和完善的異常處理。這裡使用deque雙端佇列來儲存森林中樹根節點,使用庫函式sort來對根節點依權值排序。這裡也可以使用我們之前介紹的小頂堆來完成工作。
3.4 哈夫曼樹的其他操作
其他操作在前幾篇博文中都有介紹過,這裡就不再囉嗦,可以在文章底部連結取得完整的工程原始碼。
這裡貼出測試時需要的程式碼:
/*列印哈夫曼樹*/
template<typename T>
void Huffman<T>::print(HuffmanNode<T>* pnode)
{
if (pnode != nullptr)
{
cout << "當前結點:" << pnode->key<<".";
if (pnode->lchild != nullptr)
cout << "它的左孩子節點為:" << pnode->lchild->key << ".";
else cout << "它沒有左孩子.";
if (pnode->rchild != nullptr)
cout << "它的右孩子節點為:" << pnode->rchild->key << ".";
else cout << "它沒有右孩子.";
cout << endl;
print(pnode->lchild);
print(pnode->rchild);
}
};3.5 哈夫曼樹程式碼測試
我們構建上圖中的哈夫曼樹,它的四個權值分別為{10,20,30,40}:
測試程式碼:
int _tmain(int argc, _TCHAR* argv[])
{
Huffman<int> huff;
int a[] = { 10,20,30,40 };
huff.creat(a, 4); //構建一棵哈夫曼樹
huff.print(); //列印節點間關係
getchar();
return 0;
}測試結果:
當前結點:100.它的左孩子節點為:40.它的右孩子節點為:60.
當前結點:40.它沒有左孩子.它沒有右孩子.
當前結點:60.它的左孩子節點為:30.它的右孩子節點為:30.
當前結點:30.它沒有左孩子.它沒有右孩子.
當前結點:30.它的左孩子節點為:10.它的右孩子節點為:20.
當前結點:10.它沒有左孩子.它沒有右孩子.
當前結點:20.它沒有左孩子.它沒有右孩子.根據節點關係可以畫出如下二叉樹,正是上面我們構建的哈夫曼樹。
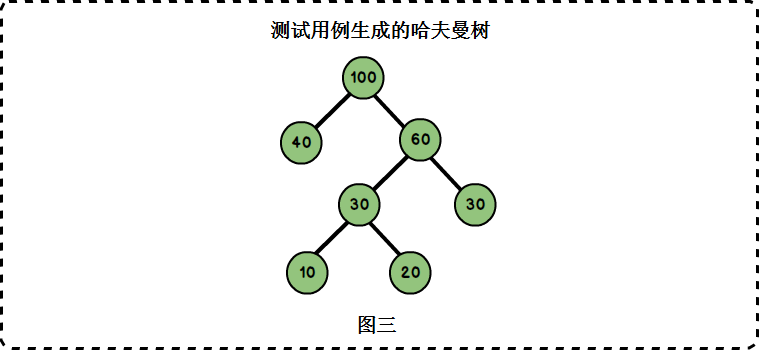
4. 再看哈夫曼編碼
為{10,20,30,40}這四個權值構建了哈夫曼編碼後,我們可以由如下規則獲得它們的哈夫曼編碼:
- 從根節點到每一個葉子節點的路徑上,左分支記為0,右分支記為1,將這些0與1連起來即為葉子節點的哈夫曼編碼。如下圖:
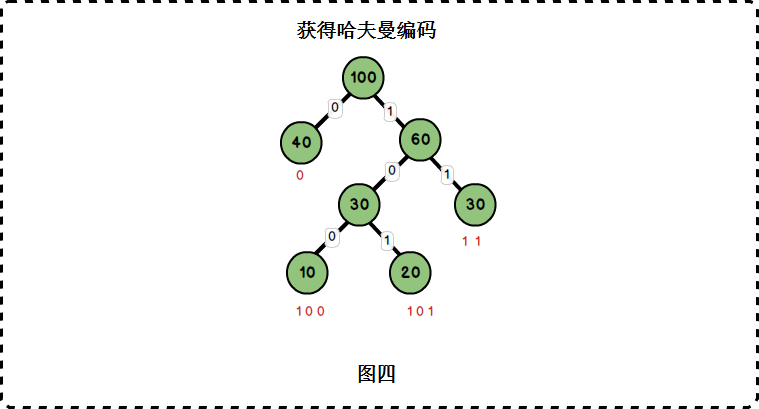
| (字母)權值 | 編碼 |
|---|---|
| 10 | 100 |
| 20 | 101 |
| 30 | 11 |
| 40 | 0 |
由此可見,出現頻率越高的字母(也即權值越大),其編碼越短。這便使編碼之後的字串的平均長度、期望值降低,從而達到無失真壓縮資料的目的。
5. 哈夫曼樹完整程式碼
相關推薦
資料結構圖文解析之:哈夫曼樹與哈夫曼編碼詳解及C++模板實現
0. 資料結構圖文解析系列 1. 哈夫曼編碼簡介 哈夫曼編碼(Huffman Coding)是一種編碼方式,也稱為“赫夫曼編碼”,是David A. Huffman1952年發明的一種構建極小多餘編碼的方法。 在計算機資料處理中,霍夫曼編碼使用變長編碼表對源符號進行編碼,出現頻率較高的源符號採用較短的編碼,
資料結構圖文解析之:樹的簡介及二叉排序樹C++模板實現.
閱讀目錄 0. 資料結構圖文解析系列 1. 樹的簡介 1.1 樹的特徵 1.2 樹的相關概念 2. 二叉樹簡介 2.1 二叉樹的定義 2.2 斜樹、滿二叉樹、完全二叉樹、二叉查詢樹 2
資料結構圖文解析之:佇列詳解與C++模板實現
正文 回到頂部 0. 資料結構圖文解析系列 回到頂部 1. 佇列簡介 回到頂部 1.1 佇列的特點 佇列(Queue)與棧一樣,是一種線性儲存結構,它具有如下特點: 佇列中的資料元素遵循“先進先出”(First In First Out)的原則,簡稱FI
資料結構圖文解析之:二叉堆詳解及C++模板實現
0. 資料結構圖文解析系列 1. 二叉堆的定義 二叉堆是一種特殊的堆,二叉堆是完全二叉樹或近似完全二叉樹。二叉堆滿足堆特性:父節點的鍵值總是保持固定的序關係於任何一個子節點的鍵值,且每個節點的左子樹和右子樹都是一個二叉堆。 當父節點的鍵值總是大於或等於任何一個子節點的鍵值時為最大堆。 當父節點的鍵值總是小於
資料結構圖文解析之:陣列、單鏈表、雙鏈表介紹及C++模板實現
0. 資料結構圖文解析系列 1. 線性表簡介 線性表是一種線性結構,它是由零個或多個數據元素構成的有限序列。線性表的特徵是在一個序列中,除了頭尾元素,每個元素都有且只有一個直接前驅,有且只有一個直接後繼,而序列頭元素沒有直接前驅,序列尾元素沒有直接後繼。 資料結構中常見的線性結構有陣列、單鏈表、雙鏈表、迴圈
資料結構圖文解析之:棧的簡介及C++模板實現
0. 資料結構圖文解析系列 1. 棧的簡介 1.1棧的特點 棧(Stack)是一種線性儲存結構,它具有如下特點: 棧中的資料元素遵守”先進後出"(First In Last Out)的原則,簡稱FILO結構。 限定只能在棧頂進行插入和刪除操作。 1.2棧的相關概念 棧的相關概念: 棧頂與棧底:允許元素
資料結構圖文解析之:直接插入排序及其優化(二分插入排序)解析及C++實現
0. 資料結構圖文解析系列 1. 插入排序簡介 插入排序是一種簡單直觀的排序演算法,它也是基於比較的排序演算法。它的工作原理是通過不斷擴張有序序列的範圍,對於未排序的資料,在已排序中從後向前掃描,找到相應的位置並插入。插入排序在實現上通常採用就地排序,因而空間複雜度為O(1)。在從後向前掃描的過程中,需要反
資料結構圖文解析之:二分查詢及與其相關的幾個問題解析
0. 資料結構圖文解析系列 1. 二分查詢簡介 二分查詢大家都不陌生,可以說除了最簡單的順序查詢之外,我們第二個接觸的查詢演算法就是二分查找了。順序查詢的時間複雜度是O(n),二分查詢的時間複雜度為O(logn)。在面試中二分查詢被考察的概率還是比較高的,上次去面試時就遇到手寫二分查詢的題目。二分查詢不難,
資料結構之:AVL樹詳解及C++模板實現
AVL樹簡介AVL樹的名字來源於它的發明作者G.M. Adelson-Velsky 和 E.M. Landis。AVL樹是最先發明的自平衡二叉查詢樹(Self-Balancing Binary Search Tree,簡稱平衡二叉樹)。一棵AVL樹有如下必要條件:條件一:它必
資料結構——第二章樹和森林:04哈夫曼樹與哈夫曼編碼
1.結點的路徑長度:從根結點到該結點的路徑上分支的數目。 2.樹的路徑長度:樹中每個結點的路徑長度之和。 3.樹的帶權路徑長度:樹中所有葉子結點的帶權路徑長度之和WPL(T) = ∑wklk(對所有葉子結點) 4.最優樹:在所有含n個結點,並帶相同權值的m叉樹中,必存在一棵其帶權路徑長度取最小值的樹,稱
#資料結構與演算法學習筆記#PTA17:哈夫曼樹與哈夫曼編碼 Huffman Tree & Huffman Code(C/C++)
2018.5.16 最近一段時間忙於實驗室各種專案和輔導員的各種雜活,間隔了半周沒有耐下心學習。導師最近接了一個要PK京東方的專案讓我來做總負責,確實是很驚喜了。責任心告訴我不能把工作做水了,但是還是嘗試把實權移交給師兄們比較好。 這道題可以說是樹這塊的壓軸題了,無論是程
數據結構——第二章樹和森林:04哈夫曼樹與哈夫曼編碼
一個 例如 stat state 森林 ont 技術 圖片 http 1.結點的路徑長度:從根結點到該結點的路徑上分支的數目。 2.樹的路徑長度:樹中每個結點的路徑長度之和。 3.樹的帶權路徑長度:樹中所有葉子結點的帶權路徑長度之和WPL(T) = ∑wklk(對所有葉子結
資料結構知識整理 - 哈夫曼樹與哈夫曼編碼
主要內容 基本概念 構造思路 儲存結構 構造演算法 哈夫曼編碼的引入 求哈夫曼編碼 基本概念 1)路徑:由一個結點到另一個結點之間的所有分支共同構成。 2)路徑長度:結點之間的分支數目。 3)樹的路徑長度:從樹的根
資料結構-2-哈夫曼樹與哈夫曼編碼 原理詳解
首先,介紹下什麼是哈夫曼樹。哈夫曼樹又稱最優二叉樹, 是一種帶權路徑長度最短的二叉樹。所謂樹的帶權路徑長度,就是樹中所有的葉結點 的權值乘上其到根結點的 路徑長度(若根結點為0層,葉結點到根結點的路徑長度 為葉結點的層數)。樹的帶權路徑長度記為WPL= (W1*L1+W
資料結構和演算法分析:第四章 樹
4.1預備知識 樹(tree)可以用幾種方式定義。定義樹的一種自然的方式使遞迴的方式。一棵樹使一些節點的集合。這個集合可以是空集;若不是空集,則樹由稱做為根(root)的節點r以及0個或多個非空的樹集合T1、T2、T3組成,這些子樹的每一課根都被來自根r的一條又
淺談演算法和資料結構(7):二叉查詢樹
前文介紹了符號表的兩種實現,無序連結串列和有序陣列,無序連結串列在插入的時候具有較高的靈活性,而有序陣列在查詢時具有較高的效率,本文介紹的二叉查詢樹(Binary Search Tree,BST)這一資料結構綜合了以上兩種資料結構的優點。 二叉查詢樹具有很高的靈活性
5.2哈夫曼樹——哈夫曼樹與哈夫曼編碼
node i++ insert 編碼 urn all IV right style #include <stdio.h> #include <stdlib.h> struct TreeNode{ int Weight; Huffm
(資料結構排序的實驗四)快速,冒泡,簡單選擇,直接插入排序的c語言實現!!
<span style="font-size:18px;"><span style="font-size:18px;"><span style="font-size:18px;"><span style="font-size:18p
哈夫曼樹與哈夫曼編碼(C語言程式碼實現)
在一般的資料結構的書中,樹的那章後面,著者一般都會介紹一下哈夫曼(HUFFMAN)樹和哈夫曼編碼。哈夫曼編碼是哈夫曼樹的一個應用。哈夫曼編碼應用廣泛,如 JPEG中就應用了哈夫曼編碼。 首先介紹什麼是哈夫曼樹。哈夫曼樹又稱最優二叉樹,是一種帶權路徑長度最短的二叉樹。所謂
哈弗曼樹與哈夫曼編碼
目錄 一、什麼是哈夫曼樹(Huffman Tree) 1.1 哈夫曼樹的定義 二、哈夫曼樹的構造 2.1 哈夫曼樹的特點 三、哈夫曼編碼 3
