定義

給定n個權值作為n個葉子結點，構造一棵二叉樹，若帶權路徑長度達到最小，稱這樣的二叉樹為最優二叉樹，也稱為哈夫曼樹(Huffman Tree)。

相關基本概念

路徑：從樹中一個結點到另一個結點之間的分支序列構成兩個節點間的路徑。
路徑長度：路徑上分支的條數成為路徑長度。
樹的路徑長度：從樹根到每個結點的路徑長度之和稱為樹的路徑長度。
結點的權：給樹中結點賦予一個數值，該數值稱為結點的權。
帶權路徑長度：結點到樹根間的路徑長度與結點權的乘積，稱為該結點的帶權路徑長度。
樹的帶權路徑長度：樹中所有葉子結點的帶權路徑長度之和，記為WPL。
最優二叉樹：在葉子個數n以及各葉子的權值Wk確定的條件下，樹的帶權路徑長度WPL值最小的二叉樹稱為最優二叉樹。

哈夫曼樹的建立

（1）初始化：根據給定的n個權值，構造n棵二叉樹的森林集合F={T1,T2,…,Tn}，其中每棵二叉樹只有一個權值為Wi的根節點，左右子樹均為空。
（2）找最小的樹並構造新的樹：在森林集合F中選取兩顆根的權值最小的樹作為左右子樹構造一棵新的二叉樹，新二叉樹的根結點為新增加的結點，其權值為左右子樹根的權值之和。
（3）刪除與插入：在森林集合中刪除已選取的兩棵根的權值最小的樹，同時將新構造的二叉樹加入到森林集合F中。
（4）重複（2）和（3）步驟：直到森林集合只含有一棵樹為止，這棵樹即為哈夫曼樹。

過程模擬：

報文A,B,C,D,E,F這6個字元構成，它們出現的頻度為：3 4 10 8 6 5

首先初始化，建立6棵二叉樹的森林集合

權值最小的為3和4

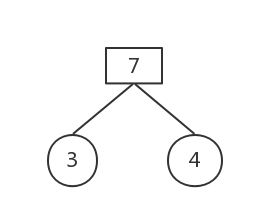
刪除這兩棵樹，構建新樹，權值為7

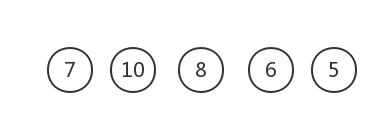
權值最小的為5和6

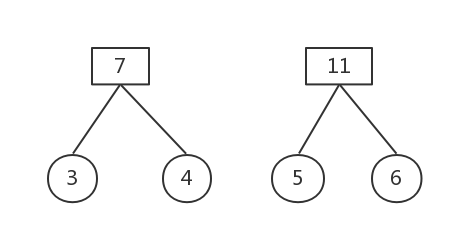
刪除這兩棵樹，構建新樹，權值為11

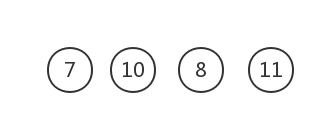
權值最小的為7和8

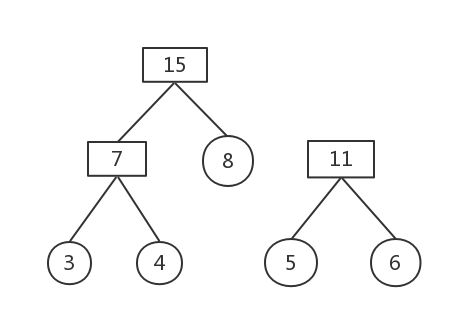
刪除這兩棵樹，構建新樹，權值為15

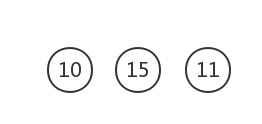
權值最小的為10和11

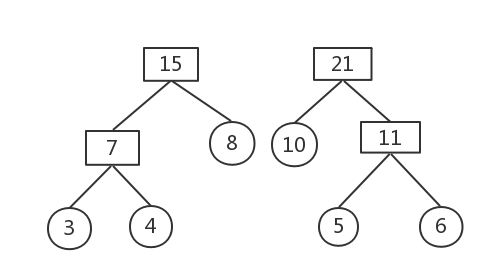
刪除這兩棵樹，構建新樹，權值為21

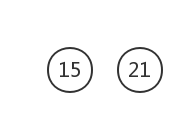
權值最小的為15和21

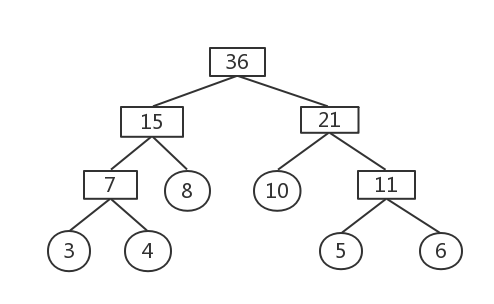
刪除這兩棵樹，構建新樹，權值為36

此時森林集合中只剩一棵樹，哈夫曼樹構建完成

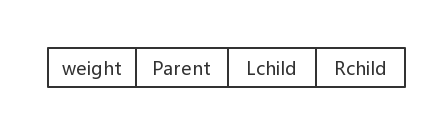
哈夫曼樹儲存結構

靜態三叉連結串列

weight：結點的權值;
Parent：雙親結點在陣列中的下標
Lchild：左孩子結點在陣列中的下標
Rchild：右孩子結點在陣列中的下標

n個葉子的哈夫曼，恰有n-1個度為2的結點，即哈夫曼樹共有2n-1個結點

型別定義如下

#define N 30
#define M 2*N-1
typedef struct{
    int weight;
    int parent,Lchild,Rchild;
}HTNode,HuffmanTree[M+1]; //0號單元不使用

哈夫曼編碼

編碼

字首編碼：同一字符集任何一個字元的編碼都不是另一個字元編碼的字首（最左字串），這種編碼稱為字首編碼。

要想有效的壓縮資訊，要使字符集中出現頻率較高的字元編碼儘可能短，出現頻率不高的字元則可以略長一些。

而觀察哈夫曼樹可以發現，權值大的葉子距離根近，權值小的距離根遠，所以可以用哈夫曼樹中跟到各葉子的路徑設計編碼。

在哈夫曼樹中約定：左分支表示符號’0’，右分支表示符號’1’。

例如，一棵哈夫曼樹如圖所示

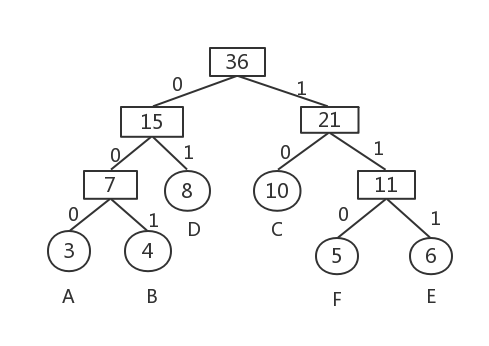
則哈夫曼編碼為：
A:000
B:001
C:10
D:01
E:111
F:110

總的來說，哈夫曼樹是WPL最小的樹，因此，哈夫曼編碼可以使資訊壓縮達到最短的編碼。哈夫曼編碼就是最優二進位制字首編碼。

演算法實現

（1）構造哈夫曼樹
（2）在哈夫曼樹上求個葉子結點的編碼

譯碼

任何經編碼壓縮、傳輸的資料，使用時均應該進行譯碼。
譯碼過程是分解、識別各個字元，還原資料的過程。

從字串頭開始掃描到尾，依次去匹配。

例項分析

給定報文，哈弗曼編碼、譯碼

題目描述

已知某段通訊報文內容，對該報文進行哈弗曼編碼，並計算平均碼長。
(1)統計報文中各字元出現的頻度。(字符集範圍為52個英文字母，空格，英文句號。報文長度<=200)
(2)構造一棵哈弗曼樹，依次給出各字元編碼結果。
(3)給字串進行編碼。
(4)給編碼串進行譯碼。
(5)計算平均碼長。
規定：
(1)結點統計：以ASCII碼的順序依次排列，例如：空格，英文句號，大寫字母，小寫字母。
(2)構建哈弗曼樹時：左子樹根結點權值小於等於右子樹根結點權值。
(3)選擇的根節點權值相同時，前者構建為雙親的左孩子，後者為右孩子。
(4)生成編碼時：左分支標0，右分支標1。

輸入

第一部分：報文內容，以’#’結束。
第二部分：待譯碼的編碼串。

輸出

依次輸出報文編碼串、譯碼串、平均碼長，三者之間均以換行符間隔。
平均碼長，保留小數點2位。

解題思路

（1）統計各個字元出現的頻度，在存權值時，也要存下來該字元
（2）構建哈夫曼樹
（3）哈夫曼編碼
（4）哈夫曼譯碼

程式碼實現

具體分析在程式碼中註釋，比較清晰

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<math.h>

#define N 30
#define M 2*N-1
typedef struct{
    int weight;
    int parent,Lchild,Rchild;
}HTNode,HuffmanTree[M+1];

typedef char** huffmanCode;

void Select(HuffmanTree ht,int j,int *s1,int *s2);//找出森林集合中根權值最小的兩個
void CrtHuffmanTree(HuffmanTree ht, int w[], int n);//構建哈夫曼樹
void CrtHuffmanCode1(HuffmanTree ht,huffmanCode hc,int n);//哈夫曼編碼
int find_code(huffmanCode hc,int n,char *dest,int *result);//在生成的哈夫曼編碼中查詢目標

//找出森林集合中根權值最小的兩個
void Select(HuffmanTree ht,int j,int *s1,int *s2)
{
    int i; 
    //int佔4個位元組，最大為2147483647
    int min = 2147483647;
    for(i=1;i<=j;i++){
        if((ht[i].parent == 0) && ht[i].weight < min){
            min = ht[i].weight;
            *s1 = i;
        }

    }
    int lessmin = 2147483647;
    for(i=1;i<=j;i++){
        if((ht[i].parent == 0) && ht[i].weight < lessmin && i != *s1){
        //下標不能相同
            lessmin = ht[i].weight;
            *s2 = i;
        }
    }
}


//建立哈夫曼樹
void CrtHuffmanTree(HuffmanTree ht, int w[], int n)
{
    int m,i;
    m = 2*n-1;
    for(i=1;i<=n;i++){ 
        ht[i].weight = w[i];//初始化前n個元素成為根結點
        ht[i].parent = 0;
        ht[i].Lchild = 0;
        ht[i].Rchild = 0;
    }
    for(i=n+1;i<=m;i++){    //初始化後n-1個元素
        ht[i].weight = 0;
        ht[i].parent = 0;
        ht[i].Lchild = 0;
        ht[i].Rchild = 0;
    }
    for(i=n+1;i<=m;i++)    //從第n+1個元素開始構造新結點
    {
        int s1,s2;
        //在ht的前i-1項中選擇雙親為0且全值較小的兩結點s1,s2
        Select(ht,i-1,&s1,&s2);
        ht[i].weight = ht[s1].weight + ht[s2].weight;//建立新結點，賦權值
        ht[i].Lchild = s1;
        ht[i].Rchild = s2;  //賦新結點左右孩子的指標
        ht[s1].parent = i;
        ht[s2].parent = i;  //改s1,s2的雙親指標
    }
}

//哈夫曼編碼
void CrtHuffmanCode1(HuffmanTree ht,huffmanCode hc,int n)
{
    //從葉子到根，逆向求各葉子結點的編碼
    char *cd;
    int start,i,c,p;
    cd = (char * )malloc(n*sizeof(char ));//臨時編碼陣列
    cd[n-1] = '\0';          //從後向前逐位求編碼，首先放置結束符
    for(i=1;i<=n;i++)        //從每個葉子開始，求相應的哈夫曼編碼
    {
        start = n-1;
        c = i;
        p = ht[i].parent;    //c為當前節點，p為其雙親
        while(p!=0){
            --start;
            if(ht[p].Lchild == c)
                cd[start] = '0';//左分支為'0'
            else
                cd[start] = '1';//右分支為'1'
            c = p;
            p = ht[p].parent;   //上溯一層 
        }
        hc[i] = (char *)malloc((n-start)*sizeof(char)); //動態申請編碼空間
        strcpy(hc[i],&cd[start]);                       //複製編碼
    }
}

//在生成的哈夫曼編碼中查詢目標
int find_code(huffmanCode hc,int n,char *dest,int *result)
{
    int i ;
    for(i=1;i<=n;i++){
        if(strcmp(dest,hc[i])==0){
            *result = i;
            return 1;
        }
    }
    return 0;
}

//主函式
int main(void)
{
    HuffmanTree ht;
    huffmanCode hc;
    int n,i;
    int w[100];     //用來存取權值
    int chlist[100];//用來存取相應的字元

    int cal[128] = {0};
    char str[10001];
    char code[10001];
    char tmp;
    while((tmp=getchar())!='#')
    {
        str[i] = tmp;
        i++;
    }
    str[i] = '\0';

    getchar();
    gets(code);

    //計算各個字元出現的頻度
    for(i=0;i<strlen(str);i++)
        cal[str[i]]++;

    //將各個字元及權值存下來
    int j = 1;
    for(i=32;i<=122;i++){
    //空格為32,z為122，題中所出現的字元都在這個範圍中
        if(cal[i]>0){
            w[j] = cal[i];
            chlist[j] = i;
            j++;
        }
    }

    //計算字元個數並構建哈夫曼樹
    n=j-1; 
    CrtHuffmanTree(ht,w,n);

    //存取哈夫曼編碼
    hc = malloc(sizeof(char)*(n+1)*(n+1));
    CrtHuffmanCode1(ht,hc,n);

    //編碼，並計算編碼結果的總長度
    long long codelength = 0;
    for(i=0;i<strlen(str);i++){
        for(int x=1;x<=n;x++){
            if(str[i]== chlist[x]){
                printf("%s",hc[x]);
                codelength +=strlen(hc[x]); 
                break;
            }
        }
    }
    printf("\n");

    //譯碼
    char temp[100];
    int result;
    int k = 0;
    for(i=0;i<strlen(code);i++){
        temp[k] = code[i];
        if(find_code(hc,n,temp,&result)){//看是否匹配
            putchar(chlist[result]);
            k = 0;
            memset(&temp,0,sizeof(temp));//若是匹配要輸出結果，並將臨時陣列置空
        }
        else{
            k++;                        //不匹配將下一個字元新增進來再判斷
        }
    }
    printf("\n");

    //輸出平均碼長，平均碼長為：編碼總長/原始資料長度
    printf("%0.2f\n",(codelength*1.0)/strlen(str));

    free(hc);//要注意malloc和free要搭配使用，學習了

    return 0;
}

關於優化

可以在存取哈夫曼編碼時採用鍵值對，省去查詢編碼時的遍歷。