對於使用機器學習解決的大多數常見問題，通常有多種可用的模型。每個模型都有自己的獨特之處，並隨因素變化而表現不同。

每個模型在“驗證/測試”資料集上來評估效能，效能衡量使用各種統計量如準確度（accuracy），精度（precision），召回率（recall）等。選擇的統計量通常針對特定應用場景和用例。 對於每個應用場景，選擇一個能夠客觀比較模型的度量指標非常重要。

本文將介紹目標檢測（Object Detection）問題中的最常用評估指標-Mean Average Precision，即mAP。

大多數時候，這些指標很容易理解和計算。例如，在二元分類中，精確度和召回率是一個一個簡單直觀的統計量。然而，目標檢測是一個非常不同且有趣的問題。即使你的目標檢測器在圖片中檢測到貓，但如果你無法定位，它也沒有用處。由於你要預測的是影象中各個物體是否出現及其位置，如何計算mAP將非常有趣。

在講解mAP之前，我們先定義目標檢測問題。

一、目標檢測問題

在目標檢測問題中，給定一個影象，找到它所包含的物體，找到它們的位置並對它們進行分類。目標檢測模型通常是在一組特定的類集合上進行訓練的，所以模型只會定位和分類影象中的那些類。另外，物件的位置通常採用矩形邊界框表示。因此，目標檢測涉及影象中物體的定位和分類。

下面所述的Mean Average Precision特別適用於同時預測物體位置及類別的演算法。 因此，從圖1可以看出，它對評估定位模型、目標檢測模型和分割模型非常有用。

二、評估目標檢測模型

1. 為什麼是mAP?

目標檢測問題中的每個圖片都可能包含一些不同類別的物體。如前所述，需要評估模型的物體分類和定位效能。因此，用於影象分類問題的標準指標precision不能直接應用於此。 這就是為什麼需要mAP。 我希望讀完這篇文章後，你將能夠理解它的含義。

2. 關於Ground Truth

對於任何演算法，評估指標需要知道ground truth（真實標籤）資料。 我們只知道訓練、驗證和測試資料集的ground truth。對於目標檢測問題，ground truth包括影象中物體的類別以及該影象中每個物體的真實邊界框。

這裡給出了一個實際圖片（jpg、png等格式），以及相應的文字註釋（邊界框座標(x, y, w, h)和類別），如圖中紅色框以及文字標籤所示。

對於這個特殊例子，模型在訓練時需要原始的圖片：

以及ground truth的3個座標及類別（這裡假定圖片大小是1000x800px，所有的座標值都是以畫素為單位的近似值）：

下面讓我們動一下手，去看如何計算mAP。這裡我們不談論不同的目標檢測演算法，假定我們已經有了一個訓練好的模型，現在只需要在驗證集上評估其效能。

三、mAP含義及計算

前面展示了原始影象和以及對應的ground truth。訓練集和驗證集中所有影象都以此方式標註。

訓練好的目標檢測模型會給出大量的預測結果，但是其中大多數的預測值都會有非常低的置信度（confidence score），因此我們只考慮那些置信度高於某個閾值的預測結果。

將原始圖片送入訓練好的模型，在經過置信度閾值篩選之後，目標檢測演算法給出帶有邊界框的預測結果：

現在，由於我們人類是目標檢測專家，我們可以知道這些檢測結果大致正確。但我們如何量化呢？我們首先需要判斷每個檢測的正確性。這裡採用IoU（Intersection over Union），它可以作為評價邊界框正確性的度量指標。 這是一個非常簡單的指標。從名稱看，有些人會發現這個名字是自解釋的，但我們需要更好的解釋。這裡會以簡短的方式解釋IoU，如果想深入理解，可以參考Adrian Rosebrock的這篇文章(Intersection over Union (IoU) for object detection)。

1. IoU

IoU是預測框與ground truth的交集和並集的比值。這個量也被稱為Jaccard指數，並於20世紀初由Paul Jaccard首次提出。為了得到交集和並集，我們首先將預測框與ground truth放在一起，如圖所示。

對於每個類，預測框和ground truth重疊的區域是交集，而橫跨的總區域就是並集。其中horse類的交集和並集如下圖所示（這個例子交集比較大）：

其中藍綠色部分是交集，而並集還包括橘色的部分。那麼，IoU可以如下計算：

2. 鑑別正確的檢測結果並計算precision和recall

為了計算precision和recall，與所有機器學習問題一樣，我們必須鑑別出True Positives（真正例）、False Positives（假正例）、True Negatives（真負例）和 False Negatives（假負例）。

為了獲得True Positives and False Positives，我們需要使用IoU。計算IoU，我們從而確定一個檢測結果（Positive）是正確的（True）還是錯誤的（False）。最常用的閾值是0.5，即如果IoU> 0.5，則認為它是True Positive，否則認為是False Positive。而COCO資料集的評估指標建議對不同的IoU閾值進行計算，但為簡單起見，我們這裡僅討論一個閾值0.5，這是PASCAL VOC資料集所用的指標。

為了計算Recall，我們需要Negatives的數量。由於圖片中我們沒有預測到物體的每個部分都被視為Negative，因此計算True Negatives比較難辦。但是我們可以只計算False Negatives，即我們模型所漏檢的物體。

另外一個需要考慮的因素是模型所給出的各個檢測結果的置信度。通過改變置信度閾值，我們可以改變一個預測框是Positive還是 Negative，即改變預測值的正負性。基本上，閾值以上的所有預測（Box + Class）都被認為是Positives，並且低於該值的都是Negatives。

對於每一個圖片，ground truth資料會給出該圖片中各個類別的實際物體數量。我們可以計算每個Positive預測框與ground truth的IoU值，並取最大的IoU值，認為該預測框檢測到了那個IoU最大的ground truth。然後根據IoU閾值，我們可以計算出一張圖片中各個類別的正確檢測值（True Positives, TP）數量以及錯誤檢測值數量（False Positives, FP）。據此，可以計算出各個類別的precision：

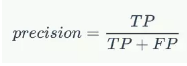
既然我們已經得到了正確的預測值數量（True Positives），也很容易計算出漏檢的物體數（False Negatives, FN）。據此可以計算出Recall（其實分母可以用ground truth總數）：

3. 計算mAP

mAP這個術語有不同的定義。此度量指標通常用於資訊檢索和目標檢測領域。然而這兩個領域計算mAP的方式卻不相同。這裡我們只談論目標檢測中的mAP計算方法。

在目標檢測中，mAP的定義首先出現在PASCAL Visual Objects Classes(VOC)競賽中，這個大賽包含許多影象處理任務，詳情可以參考這個http://homepages.inf.ed.ac.uk/ckiw/postscript/ijcv_voc09.pdf（裡面包含各個比賽的介紹以及評估等）。

前面我們已經講述瞭如何計算Precision和Recall，但是，正如前面所述，至少有兩個變數會影響Precision和Recall，即IoU和置信度閾值。IoU是一個簡單的幾何度量，可以很容易標準化，比如在PASCAL VOC競賽中採用的IoU閾值為0.5，而COCO競賽中在計算mAP較複雜，其計算了一系列IoU閾值（0.05至0.95）下的mAP。但是置信度卻在不同模型會差異較大，可能在我的模型中置信度採用0.5卻等價於在其它模型中採用0.8置信度，這會導致precision-recall曲線變化。為此，PASCAL VOC組織者想到了一種方法來解決這個問題，即要採用一種可以用於任何模型的評估指標。在paper中，他們推薦使用如下方式計算Average Precision（AP）：

For a given task and class, the precision/recall curve is computed from a method’s ranked output. Recall is defined as the proportion of all positive examples ranked above a given rank. Precision is the proportion of all examples above that rank which are from the positive class. The AP summarises the shape of the precision/recall curve, and is defined as the mean precision at a set of eleven equally spaced recall levels [0,0.1,…,1]:

可以看到，為了得到precision-recall曲線，首先要對模型預測結果進行排序（ranked output，按照各個預測值置信度降序排列）。那麼給定一個rank，Recall和Precision僅在高於該rank值的預測結果中計算，改變rank值會改變recall值。這裡共選擇11個不同的recall（[0, 0.1, ..., 0.9, 1.0]），可以認為是選擇了11個rank，由於按照置信度排序，所以實際上等於選擇了11個不同的置信度閾值。那麼，AP就定義為在這11個recall下precision的平均值，其可以表徵整個precision-recall曲線（曲線下面積）。

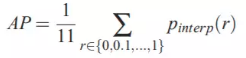
另外，在計算precision時採用一種插值方法（interpolate）：

The precision at each recall level r is interpolated by taking the maximum precision measured for a method for which the corresponding recall exceeds r:The intention in interpolating the precision/recall curve in this way is to reduce the impact of the “wiggles” in the precision/recall curve, caused by small variations in the ranking of examples.

及對於某個recall值r，precision值取所有recall>r中的最大值（這樣保證了p-r曲線是單調遞減的，避免曲線出現搖擺）:

不過這裡VOC資料集在2007年提出的mAP計算方法，而在2010之後卻使用了所有資料點，而不是僅使用11個recall值來計算AP（詳細參考這篇http://host.robots.ox.ac.uk/pascal/VOC/pubs/everingham15.pdf）：

Up until 2009 interpolated average precision (Salton and Mcgill 1986) was used to evaluate both classification and detection. However, from 2010 onwards the method of computing AP changed to use all data points rather than TREC-style sampling (which only sampled the monotonically decreasing curve at a fixed set of uniformly-spaced recall values 0, 0.1, 0.2,…, 1). The intention in interpolating the precision–recall curve was to reduce the impact of the ‘wiggles’ in the precision–recall curve, caused by small variations in the ranking of examples. However, the downside of this interpolation was that the evaluation was too crude to discriminate between the methods at low AP.

對於各個類別，分別按照上述方式計算AP，取所有類別的AP平均值就是mAP。這就是在目標檢測問題中mAP的計算方法。可能有時會發生些許變化，如COCO資料集採用的計算方式更嚴格，其計算了不同IoU閾值和物體大小下的AP（詳情參考http://cocodataset.org/#detection-eval）。

當比較mAP值，記住以下要點：

• mAP通常是在一個數據集上計算得到的。

• 雖然解釋模型輸出的絕對量化並不容易，但mAP作為一個相對較好的度量指標可以幫助我們。 當我們在流行的公共資料集上計算這個度量時，該度量可以很容易地用來比較目標檢測問題的新舊方法。

• 根據訓練資料中各個類的分佈情況，mAP值可能在某些類（具有良好的訓練資料）非常高，而其他類（具有較少/不良資料）卻比較低。所以你的mAP可能是中等的，但是你的模型可能對某些類非常好，對某些類非常不好。因此，建議在分析模型結果時檢視各個類的AP值。這些值也許暗示你需要新增更多的訓練樣本。

四、程式碼實現

Facebook開源的Detectron包含VOC資料集的mAP計算(https://github.com/facebookresearch/Detectron/blob/05d04d3a024f0991339de45872d02f2f50669b3d/lib/datasets/voc_eval.py)，這裡貼出其核心實現，以對mAP的計算有更深入的理解。首先是precision和recall的計算：

# 按照置信度降序排序
sorted_ind = np.argsort(-confidence)
BB = BB[sorted_ind, :]   # 預測框座標
image_ids = [image_ids[x] 
for x in sorted_ind] # 各個預測框的對應圖片id# 便利預測框，並統計TPs和FPs
nd = len(image_ids)
tp = np.zeros(nd)
fp = np.zeros(nd)
for d in range(nd):    
R = class_recs[image_ids[d]]    
bb = BB[d, :].astype(float)    
ovmax = -np.inf    
BBGT = R['bbox'].astype(float)  # ground truth    
if BBGT.size > 0:
        # 計算IoU        # intersection        
ixmin = np.maximum(BBGT[:, 0], bb[0])        
iymin = np.maximum(BBGT[:, 1], bb[1])        
ixmax = np.minimum(BBGT[:, 2], bb[2])        
iymax = np.minimum(BBGT[:, 3], bb[3])        
iw = np.maximum(ixmax - ixmin + 1., 0.)        
ih = np.maximum(iymax - iymin + 1., 0.)        
inters = iw * ih        # union        
uni = ((bb[2] - bb[0] + 1.) * (bb[3] - bb[1] + 1.) +               
(BBGT[:, 2] - BBGT[:, 0] + 1.) *               
(BBGT[:, 3] - BBGT[:, 1] + 1.) - inters)        
overlaps = inters / uni        
ovmax = np.max(overlaps)        
jmax = np.argmax(overlaps)    # 取最大的IoU    
if ovmax > ovthresh:  # 是否大於閾值        
if not R['difficult'][jmax]:  # 非difficult物體            
if not R['det'][jmax]:    # 未被檢測                
tp[d] = 1.                
R['det'][jmax] = 1    # 標記已被檢測            
else:                
fp[d] = 1.    
else:        
fp[d] = 1.# 計算
precision recallfp = np.cumsum(fp)
tp = np.cumsum(tp)rec = tp / float(npos)# avoid divide by zero in case the first detection matches a difficult# ground truth
prec = tp / np.maximum(tp + fp, np.finfo(np.float64).eps)

這裡最終得到一系列的precision和recall值，並且這些值是按照置信度降低排列統計的，可以認為是取不同的置信度閾值（或者rank值）得到的。然後據此可以計算AP：

計算各個類別的AP值後，取平均值就可以得到最終的mAP值了。但是對於COCO資料集相對比較複雜，不過其提供了計算的API，感興趣可以看一下https://github.com/cocodataset/cocoapi/blob/master/PythonAPI/pycocotools/cocoeval.py。

本文翻譯自Measuring Object Detection models - mAP - What is Mean Average Precision?(http://tarangshah.com/blog/2018-01-27/what-is-map-understanding-the-statistic-of-choice-for-comparing-object-detection-models/)，原作者保留版權。