這篇文章繼上篇機器學習經典模型簡單使用及歸一化（標準化）影響，通過將測試集label（行）錯位，將部分資料作為對未來的預測，觀察其效果。

實驗方式

• 以不同方式劃分資料集和測試集
• 使用不同的歸一化（標準化）方式
• 使用不同的模型
• 將測試集label錯位，計算出MSE的大小
• 不斷增大錯位的資料的個數，並計算出MSE，並畫圖
• 通過比較MSE（均方誤差，mean-square error）的大小來得出結論

過程及結果

資料預處理部分與上次相同。兩種劃分方式：

一、

test_sort_data = sort_data[16160:]
test_sort_target 
 
= sort_target[16160:]

_sort_data = sort_data[:16160]
_sort_target = sort_target[:16160]
sort_data1 = _sort_data[:(int)(len(_sort_data)*0.75)]
sort_data2 = _sort_data[(int)(len(_sort_data)*0.75):]
sort_target1 = _sort_target[:(int)(len(_sort_target)*0.75)]
sort_target2 = _sort_target[(int)(len(_sort_target)*0.75):]

二、

test_sort_data = sort_data[:5000]
test_sort_target = sort_target[:5000]

sort_data1 = _sort_data[5000:16060]
sort_data2 = _sort_data[16060:]
sort_target1 = _sort_target[5000:16060]
sort_target2 = _sort_target[16060:]

一開始用的第一種劃分方式，發現直接跑飛了

然後仔細想了想，觀察了上篇部落格跑出來的資料，果斷換了第二種劃分方式，發現跑出來的結果還不錯

MaxMinScaler()

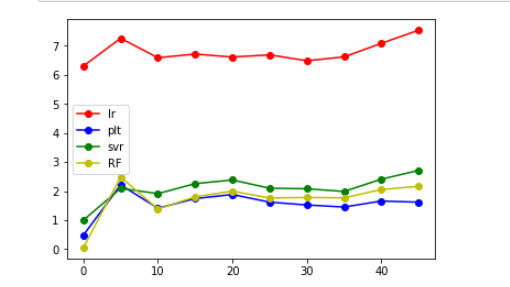
看到lr模型明顯要大，就捨棄了

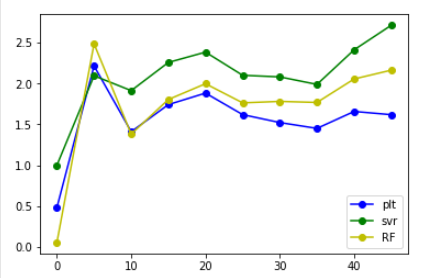
(emmmmm。。。這張圖看起來就友好很多了)

MaxAbsScaler()

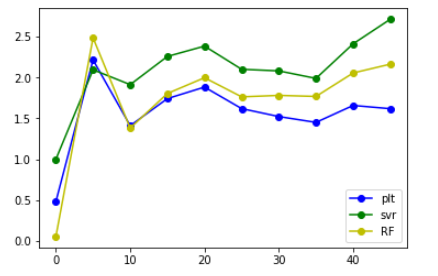
StandardScaler()

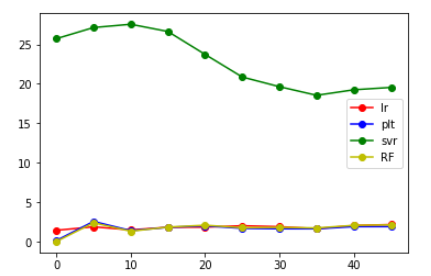
程式碼

其中大部分的程式碼都是一樣的，就是改改歸一化方式，就只放一部分了

資料預處理部分見上篇部落格

加上這一段用於畫圖

import matplotlib.pyplot as plt 
lr_plt=[]
ridge_plt=[]
svr_plt=[]
RF_plt=[]

接著，先計算不改變label時的值

from sklearn.linear_model import LinearRegression,Lasso,Ridge
from sklearn.preprocessing import MinMaxScaler,StandardScaler,MaxAbsScaler
from sklearn.metrics import mean_squared_error as mse
from sklearn.svm import SVR
from sklearn.ensemble import RandomForestRegressor
import xgboost as xgb
#最大最小歸一化
mm = MinMaxScaler()

lr = Lasso(alpha=0.5)
lr.fit(mm.fit_transform(sort_data1[new_fea]), sort_target1)
lr_ans = lr.predict(mm.transform(sort_data2[new_fea]))
lr_mse=mse(lr_ans,sort_target2)
lr_plt.append(lr_mse)
print('lr:',lr_mse)

ridge = Ridge(alpha=0.5)
ridge.fit(mm.fit_transform(sort_data1[new_fea]),sort_target1)
ridge_ans = ridge.predict(mm.transform(sort_data2[new_fea]))
ridge_mse=mse(ridge_ans,sort_target2)
ridge_plt.append(ridge_mse)
print('ridge:',ridge_mse)

svr = SVR(kernel='rbf',C=100,epsilon=0.1).fit(mm.fit_transform(sort_data1[new_fea]),sort_target1)
svr_ans = svr.predict(mm.transform(sort_data2[new_fea]))
svr_mse=mse(svr_ans,sort_target2)
svr_plt.append(svr_mse)
print('svr:',svr_mse)

estimator_RF = RandomForestRegressor().fit(mm.fit_transform(sort_data1[new_fea]),sort_target1)
predict_RF = estimator_RF.predict(mm.transform(sort_data2[new_fea]))
RF_mse=mse(predict_RF,sort_target2)
RF_plt.append(RF_mse)
print('RF:',RF_mse)

bst = xgb.XGBRegressor(learning_rate=0.1, n_estimators=550, max_depth=4, min_child_weight=5, seed=0,
                             subsample=0.7, colsample_bytree=0.7, gamma=0.1, reg_alpha=1, reg_lambda=1)
bst.fit(mm.fit_transform(sort_data1[new_fea]),sort_target1)
bst_ans = bst.predict(mm.transform(sort_data2[new_fea]))
print('bst:',mse(bst_ans,sort_target2))

先將label錯位，使得data2的第i位對應target2的第i+5位

change_sort_data2 = sort_data2.shift(periods=5,axis=0)
change_sort_target2 = sort_target2.shift(periods=-5,axis=0)
change_sort_data2.dropna(inplace=True)
change_sort_target2.dropna(inplace=True)

然後用一個迴圈不斷迭代，改變錯位的數量

mm = MinMaxScaler()

for i in range(0,45,5):
    print(i)
    lr = Lasso(alpha=0.5)
    lr.fit(mm.fit_transform(sort_data1[new_fea]), sort_target1)
    lr_ans = lr.predict(mm.transform(change_sort_data2[new_fea]))
    lr_mse=mse(lr_ans,change_sort_target2)
    lr_plt.append(lr_mse)
    print('lr:',lr_mse)
    
    ridge = Ridge(alpha=0.5)
    ridge.fit(mm.fit_transform(sort_data1[new_fea]),sort_target1)
    ridge_ans = ridge.predict(mm.transform(change_sort_data2[new_fea]))
    ridge_mse=mse(ridge_ans,change_sort_target2)
    ridge_plt.append(ridge_mse)
    print('ridge:',ridge_mse)
    
    svr = SVR(kernel='rbf',C=100,epsilon=0.1).fit(mm.fit_transform(sort_data1[new_fea]),sort_target1)
    svr_ans = svr.predict(mm.transform(change_sort_data2[new_fea]))
    svr_mse=mse(svr_ans,change_sort_target2)
    svr_plt.append(svr_mse)
    print('svr:',svr_mse)
    
    estimator_RF = RandomForestRegressor().fit(mm.fit_transform(sort_data1[new_fea]),sort_target1)
    predict_RF = estimator_RF.predict(mm.transform(change_sort_data2[new_fea]))
    RF_mse=mse(predict_RF,change_sort_target2)
    RF_plt.append(RF_mse)
    print('RF:',RF_mse)
    
#     bst = xgb.XGBRegressor(learning_rate=0.1, n_estimators=550, max_depth=4, min_child_weight=5, seed=0,
#                              subsample=0.7, colsample_bytree=0.7, gamma=0.1, reg_alpha=1, reg_lambda=1)
#     bst.fit(mm.fit_transform(sort_data1[new_fea]),sort_target1)
#     bst_ans = bst.predict(mm.transform(change_sort_data2[new_fea]))
#     print('bst:',mse(bst_ans,change_sort_target2))
    
    change_sort_target2=change_sort_target2.shift(periods=-5,axis=0)
    change_sort_target2.dropna(inplace=True)
    change_sort_data2 = change_sort_data2.shift(periods=5,axis=0)
    change_sort_data2.dropna(inplace=True)

 然後就可以畫圖了

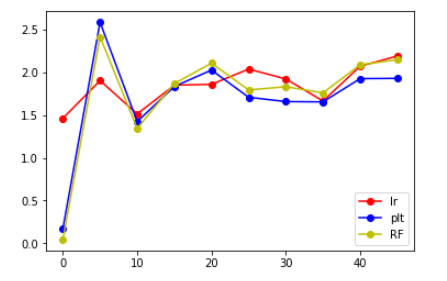
x=[0,5,10,15,20,25,30,35,40,45]
plt.plot(x,lr_plt,label='lr',color='r',marker='o')
plt.plot(x,ridge_plt,label='plt',color='b',marker='o')
plt.plot(x,svr_plt,label='svr',color='g',marker='o')
plt.plot(x,RF_plt,label='RF',color='y',marker='o')
plt.legend()
plt.show()

結果分析

從上面給出的圖來看，發現將label錯位後，相比於原來的大小還是有所增大，但是增大後的值並不是特別大，並且大致在某個範圍內浮動，大概在錯位10個label時能得到的結果是最好的。