資料預處理中歸一化（Normalization）與損失函式中正則化（Regularization）解惑
背景：資料探勘/機器學習中的術語較多，而且我的知識有限。之前一直疑惑正則這個概念。所以寫了篇博文梳理下
摘要：
1.正則化（Regularization）
1.1 正則化的目的
1.2 結構風險最小化（SRM）理論
1.3 L1範數（lasso），L2範數（ridge），ElasticNet
1.4為什麼說L1是稀疏的，L2是平滑的？
2.歸一化 （Normalization）
2.1歸一化的目的
2.1歸一化計算方法
2.2.spark ml中的歸一化
2.3 python中skelearn中的歸一化
知識總結：
1.正則化（Regularization）
1.1 正則化的目的：我的理解就是平衡訓練誤差與模型複雜度的一種方式，通過加入正則項來避免過擬合（over-fitting）。（可以引入擬合時候的龍格現象，然後引入正則化及正則化的選取，待新增）
1.2 結構風險最小化（SRM）理論: 經驗風險最小化 + 正則化項 = 結構風險最小化 經驗風險最小化（ERM），是為了讓擬合的誤差足夠小，即：對訓練資料的預測誤差很小。但是，我們學習得到的模型，當然是希望對未知資料有很好的預測能力（泛化能力），這樣才更有意義。當擬合的誤差足夠小的時候，可能是模型引數較多，模型比較複雜，此時模型的泛化能力一般。於是，我們增加一個正則化項，它是一個正的常數乘以模型複雜度的函式，aJ(f)，a>=0 用於調整ERM與模型複雜度的關係。結構風險最小化（SRM），相當於是要求擬合的誤差足夠小，同時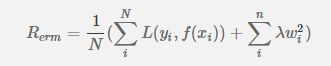
後面的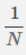
上圖的 lambda = 0表示未做正則化，模型過於複雜（存在過擬合）
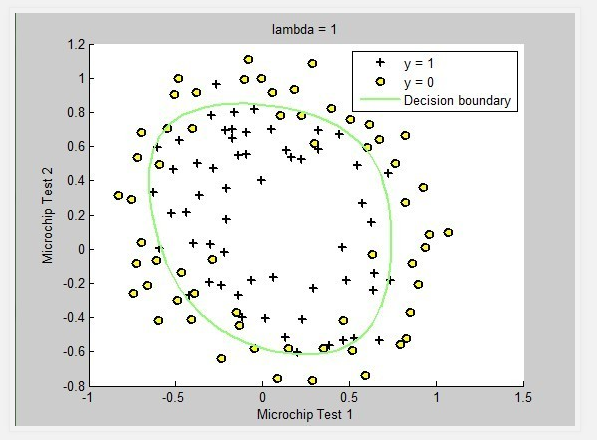上圖的 lambda = 1 添加了正則項，模型複雜度降低
1.3 正則化的L1，L2範數
L1正則化(lasso)：
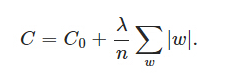，其中C0是代價函式，
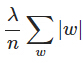是L1正則項，lambda是正則化引數
L2正則化(ridge)：（待新增：權值衰減引入）
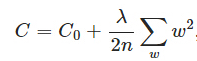，其中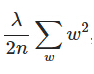
是L2正則項，lambda是正則化引數
ElasticNet 正則化:
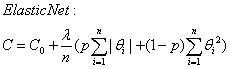
L1與L2以及ElasticNet 正則化的比較：
1.L1會趨向於產生少量的特徵，而其他的特徵都是0，而L2會選擇更多的特徵，這些特徵都會接近於0。
2.Lasso在特徵選擇時候非常有用，而Ridge就只是一種規則化而已。
3.ElasticNet 吸收了兩者的優點，當有多個相關的特徵時，Lasso 會隨機挑選他們其中的一個，而ElasticNet則會選擇兩個；並且ElasticNet 繼承 Ridge 的穩定性.
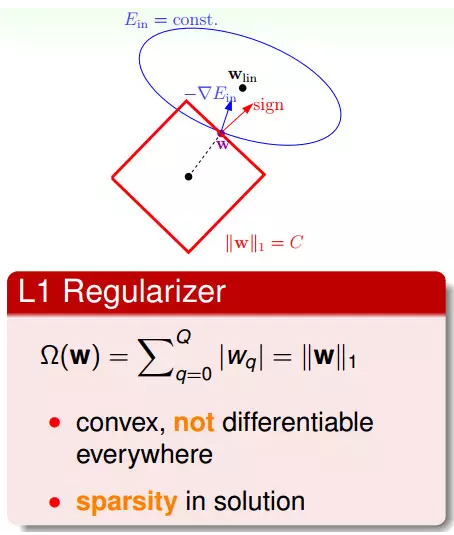
總結：結構風險最小化是一種模型選擇的策略，通過加入正則項以平衡模型複雜度和經驗誤差；更直觀的解釋——正則項就是模型引數向量（w）的範數，一般有L1，L2兩種常用的範數。 1.4為什麼說L1是稀疏的，L2是平滑的？L1 Regularizer
L1 Regularizer是用w的一範數來算，該形式是凸函式，但不是處處可微分的，所以它的最佳化問題會相對難解一些。
L1 Regularizer的最佳解常常出現在頂點上（頂點上的w只有很少的元素是非零的，所以也被稱為稀疏解sparse solution），這樣在計算過程中會比較快。
L2 Regularizer
L2 Regularizer是凸函式，平滑可微分，所以其最佳化問題是好求解的。
2.歸一化 （Normalization）
2.1歸一化的目的：
1）歸一化後加快了梯度下降求最優解的速度；
2）歸一化有可能提高精度。詳解可檢視
2.2歸一化計算方法
公式： 對於大於1的整數p, Lp norm = sum(|vector|^p)(1/p)2.3.spark ml中的歸一化
構造方法： http://spark.apache.org/docs/2.0.0/api/scala/index.html#org.apache.spark.mllib.feature.NormalizernewNormalizer(p: Double) ,其中p就是計算公式中的向量絕對值的冪指數
可以使用transform方法對Vector型別或者RDD[Vector]型別的資料進行正則化
下面舉一個簡單的例子： scala> import org.apache.spark.mllib.linalg.{Vector, Vectors}
scala> val dv: Vector = Vectors.dense(3.0,4.0)
dv: org.apache.spark.mllib.linalg.Vector = [3.0,4.0]
scala> val l2 = new Normalizer(2)
scala> l2.transform(dv)
res8: org.apache.spark.mllib.linalg.Vector = [0.6,0.8]
或者直接使用Vertors的norm方法：val norms = data.map(Vectors.norm(_, 2.0))
2.4 python中skelearn中的歸一化
from sklearn.preprocessing import Normalizer
#歸一化，返回值為歸一化後的資料
Normalizer().fit_transform(iris.data)