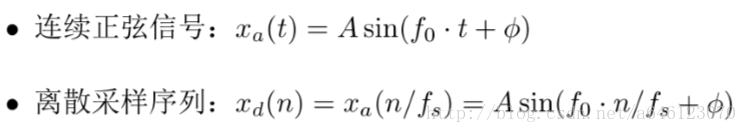MATLAB 訊號處理模擬入門實驗
MATLAB 訊號處理模擬入門實驗
實驗目的：
• 熟悉 Matlab 工具的基本用法
• 掌握 Matlab 程式碼編寫方法
• 理解序列的離散時間傅立葉變換
• 理解 DFT 結果的頻譜能量洩露
• 理解 DFT 和 DTFT 的對應關係
• 理解訊號加窗的作用
實驗內容：
• 任務1、單音正弦訊號取樣序列的時域繪圖
• 任務2、單音正弦訊號取樣序列的DFT結果繪圖
• 任務3、有限長矩形窗序列的DTFT
• 任務4、有限長正弦序列的DTFT
• 任務5、 DTFT 和 DFT 關係探尋
• 最終任務：雙音訊號頻率分析
正弦訊號及其取樣序列的數學描述如下：
模擬中需要設定的訊號配置引數：
1. 訊號取樣率 fs
2. 訊號幅度 Amp
3. 正弦訊號頻率 f
4. 正弦初始相位為 phy
5. 訊號取樣序列長度 N
任務1、單音正弦訊號取樣序列的時域繪圖
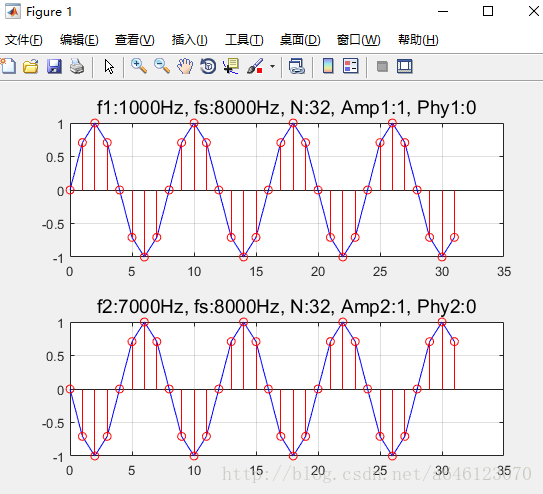
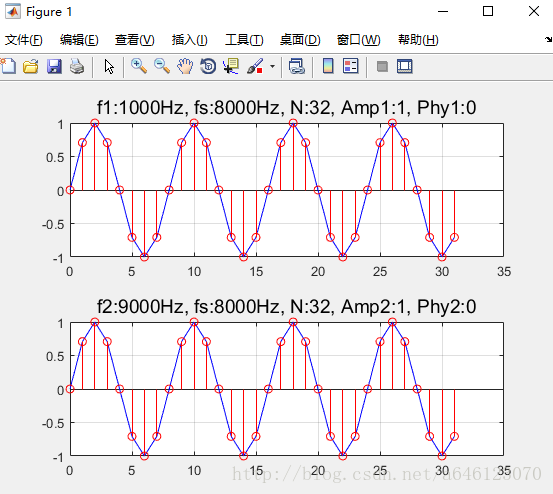
• 按照以下兩組配置引數修改程式碼
• 觀察繪製出的訊號時域圖樣
配置引數 1：
f1 = 1000; Amp1 = 1; phy1 = 0; f2 = 7000; Amp2 = 1; phy2 = 0;
配置引數 2：
f1 = 1000; Amp1 = 1; phy1 = 0; f2 = 9000; Amp2 = 1; phy2 = 0;
實驗程式碼：
% test with Matlab 2016 模擬圖：
配置引數2程式碼與配置引數1程式碼相似，只需修改具體數值，下面只給出繪圖。
• 請回答: 數字訊號處理的課本中說數字取樣訊號的歸一化角頻率 ω 的數值範圍是寬度為 2π 區間，這是為什麼？
歸一化頻率是訊號頻率除以取樣頻率的一半，如果將歸一化頻率轉換為角頻率，則將歸一化頻率乘以π ，所以歸一化角頻率是寬度為2π 的區間。
• 請自行上網搜尋關鍵字“帶通取樣定理”思考其原理和可行性
帶通取樣定理：設帶通訊號m(t),其頻率限制在fL與fH之間，頻寬為B=fH-fL，如果最小抽樣速率fs=2fH/m,m是一個不超過fH/B的最大整數，那麼m(t),可以完全由其抽樣值確定。
• 任務2、單音正弦訊號取樣序列的DFT結果繪圖
• 離散傅立葉變換 DFT
– 擁有著名的快速演算法 — FFT
– DFT的主要用途：分析訊號頻譜
• 本實驗的內容 – 計算確知訊號（正弦訊號）取樣序列的DFT譜
– 設定不同的模擬配置，觀察正弦訊號的DFT譜
• 改變DFT的計算長度
• 改變輸入正弦訊號取樣序列的頻率
• 完成實驗後思考問題 – 序列的DFT結果和其連續版本訊號的頻譜完全一致麼？
實驗程式碼：
主函式
% file: sine_1_tone_dft.m
% test with Matlab 2016
close all;
clear;
fig_fname_0 = 'sine_1_tone_dft_0.jpg';
fig_fname_1 = 'sine_1_tone_dft_1.jpg';
fig_fname_2 = 'sine_1_tone_dft_2.jpg';
fs = 8E3;
f0_0 = 500; f0_1 = 600; f0_2 = 500;
N_0 = 32 ; N_1 = 32 ; N_2 = 35 ;
% plot each case
func_sine_1_tone_dft_plot(f0_0, fs, N_0, fig_fname_0);
func_sine_1_tone_dft_plot(f0_1, fs, N_1, fig_fname_1);
func_sine_1_tone_dft_plot(f0_2, fs, N_2, fig_fname_2);
子函式
% test with Matlab 2016
% file: func_sine_1_tone_dft_plot.m
% 繪圖程式：繪製訊號取樣序列的 時域波形，
% 線性尺度DFT幅度譜，對數尺度DFT幅度譜
function func_sine_1_tone_dft_plot(f0, fs, N, fig_fname);
n_idx = [0:N-1]; % 訊號序列的下標向量
x = sin(2*pi*f0/fs*n_idx); % 生成正弦訊號序列
y = abs(fft(x)); y_dB = 20*log10(1E-6+y); % 計算 DFT 結果線性幅度譜及對數幅度譜
h = figure;
% 繪圖橫軸左右邊界
x_left = -1; x_right = N+1;
% 時域繪圖
subplot(3,1,1);
stem(n_idx, x); grid on; hold;
plot(n_idx, x); xlim([x_left, x_right]);
xlim([x_left, x_right]);
title_str = ['f0:', num2str(f0),'Hz, ', 'fs:', num2str(fs),'Hz, ' 'N:', num2str(N)];
title(title_str, 'fontsize',14);
% 繪圖線性幅度譜
subplot(3,1,2); stem(n_idx, y); grid on;
xlim([x_left, x_right]);
title_str = ['DFT Magtitude Linear Scale, '];
title_str = [title_str, ' Max:', num2str(max(y)), ', Min:', num2str(min(y))];
title(title_str, 'fontsize',14);
% 繪圖對數幅度譜
subplot(3,1,3); stem(n_idx, y_dB); grid on;
xlim([x_left, x_right]);
title_str = ['DFT Magtitude dB Scale, '];
title_str = [title_str, ' Max:', num2str(max(y_dB)), ', Min:', num2str(min(y_dB))];
title(title_str, 'fontsize',14);
print(h, '-djpeg', fig_fname); % 儲存繪圖結果檔案
end• 實驗程式碼說明
– sine_1_tone_dft.m ： 實驗入口程式碼
– 函式說明
• function func_sine_1_tone_dft_plot(f0, fs, N, fig_fname);
• 功能：繪製正弦訊號取樣序列的DFT幅度譜，然後儲存曲線圖
• 引數 f0：正弦訊號頻率
• 引數 fs ：取樣率
• 引數 N ：序列長度
• 引數 fig_fname：儲存的繪圖檔名（jpg格式）
模擬圖：
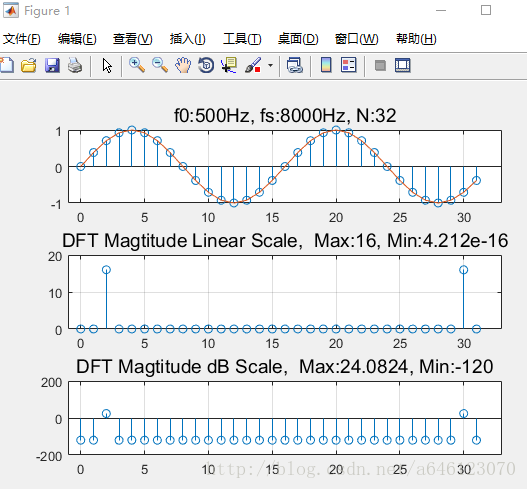
取樣序列中包含了2個完整的訊號週期的取樣值，DFT幅度譜分析結果有2根峰值譜線，其餘位置上均是0。
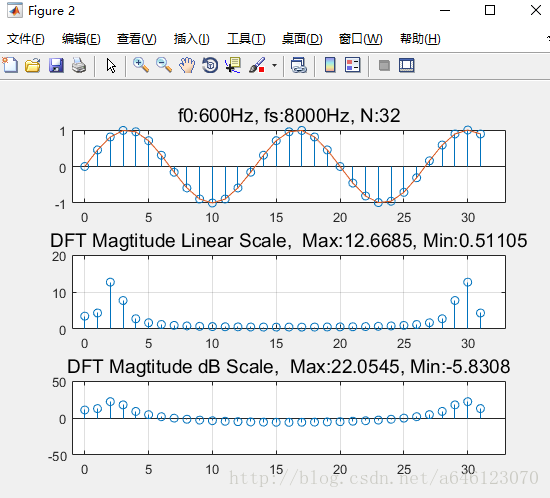
取樣序列中包含了2個完整的訊號週期，以及 一個不完整訊號週期的取樣值，DFT幅度譜分析結果有2根極大值譜線，但是其餘位置上不為0。
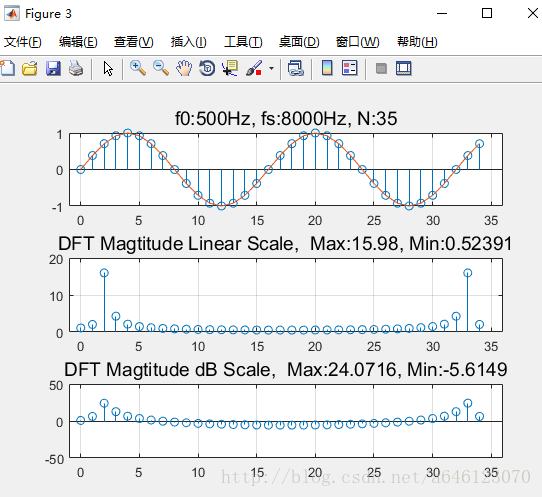
取樣序列中包含了2個完整的訊號週期，以及 一個不完整訊號週期的取樣值，DFT幅度譜 分析結果有2根極大值譜線，但是其餘位置上不為0。
總結規律
– 在取樣序列包含整數個訊號週期的情況下，訊號取樣後的DFT分析結果和連續訊號的傅立葉變換頻譜最相似。
–頻譜洩露的最根本原因還在於訊號的非週期截斷，可以從時域和頻域兩方面來理解：
(1) 從時域上，傅立葉變換的潛在假設為待處理的有限訊號為週期性無限訊號的週期主體，即假設原始訊號為當前有限訊號的無限個週期延拓。因此，舉個簡單例子。我們擷取50HZ 正弦訊號的一個週期，其無限延拓就是最原始的50HZ正弦訊號，因此一個週期的有限訊號即可代表其原始的無限訊號；若擷取的有限訊號不是50HZ訊號的整數倍週期，可知該有限訊號的無限延拓不可完全的復原原始的50HZ無限訊號，其首尾連線處出現斷續，從而引入高次諧波分量，產生頻譜洩露。
(2)從頻域上，假設訊號週期T，頻率F， 取樣週期Ts，取樣頻率Fs， 取樣點數N，則整數週期截斷的物理表達為N*Ts = m*T <=> N*1/Fs=m*1/F <=> F=m*Fs/N. 在頻域上，Fs對應2π，且頻域解析度為2π/N。 因此F=m*Fs/N意義為訊號頻率在FFT後的第m根譜線上。反之，當非週期截斷時，則無法滿足F=m*Fs/N，訊號的頻率成分分散k*2π/N的頻率點上。
由於工程實際處理的訊號基本為非平穩多諧波訊號，因此頻譜洩露不可避免。為了改善頻譜洩露，可行的方向包含以下幾點：
1. 增大FFT變換的點數N。 通過增大N，一方面提高頻域解析度，更大可能滿足F=m*Fs/N， 另一方面，壓縮sinc的瓣寬，降低洩露水平。
2. 選用合適的窗函式。根據不同的需求來選擇不同特性的窗函式，主瓣寬但旁瓣衰減大的窗或是主瓣窄但旁瓣相對衰減小的窗。
• 任務3、有限長矩形窗序列的DTFT
背景知識：DTFT的重要性
• 計算機的侷限性
– 只能計算有限長的資料（無限長的資料，只存在於理論分析的世界裡）
– 只能計算離散化的資料（連續變數的函式，計算其函式值時，只能 在離散化的自變數的抽樣點上進行）
• 離散時間序列傅立葉變換（DTFT）的重要性
– 在無窮長的尺度上累加
– 輸出的結果函式是連續變數函式
– 確定的離散序列，無論有限長、無限長
• 其DTFT變換結果，具有理論唯一性
– 理論唯一性的重要在於：
• 可以使用多種工程計算方法無限逼近
• 可以用來檢驗工程計算方法的正確性和有效性
實驗程式碼：
主函式：
% file: plot_dtft.m
% test with Matlab 2007
clc
clear
close all
w_min = -1*pi;
w_max = 1*pi;
w_delta = pi/1000;
n_min = 0;
n_max = 3 ;
n = [n_min:1:n_max];
w = [w_min:w_delta:w_max];
N = length(n);
x = ones(1,N);
x_dscp_str = 'x(n)';
Y = func_calc_dtft(x, n, w);
h = func_plot_dtft(x,n,w,Y, x_dscp_str);子函式1：
% file: func_plot_dtft.m
% test with Matlab 2007
% Y[w] = DTFT(x[n]);
% plot time sequence x[n], real/imag part of Y[w], abs of Y[w]
function h = func_plot_dtft(x,n,w,Y, x_dscp_str);
h = figure;
N = length(n);
n_min = min(n);
n_max = max(n);
w_min = min(w);
w_max = max(w);
N_w = length(w);
w_delta = (w_max-w_min)/(N_w-1);
w_x_tick_delta = 1*pi/4;
w_x_tick = get_w_x_tick_vec(w_min, w_max, w_x_tick_delta);
w_x_tick_label_cell = get_w_x_tick_label_cell(w_x_tick, w_x_tick_delta);
Y_real = real(Y); Y_imag = imag(Y); Y_abs = abs(Y);
subplot(2,2,1);
title_str = [x_dscp_str, ', n \in [',int2str(n_min),',', int2str(n_max), ...
'], ', int2str(N), ' samples'];
stem(n, x, 'fill'); title(title_str, 'fontsize',14);
y_lim_max = 1.1*max(abs(x)); y_lim_min = -y_lim_max;
grid on; xlim([n_min-1,n_max+1]); ylim([y_lim_min, y_lim_max]);
subplot(2,2,2);
Left_str = get_tick_str((w_min/pi),1,'\pi');
Right_str = get_tick_str((w_max/pi),1,'\pi');
w_xLabelStr =['\omega: [', Left_str,',', Right_str, ']'];
title_str = ['\{X(e^{j\omega})\}, \Delta\omega = \pi/', num2str(pi/w_delta)];
plot(w, Y_real);title(['Re', title_str], 'fontsize',14);
grid on; xlim([w_min,w_max]);ylim([(min(Y_real)-0.5),(max(Y_real)+0.5)]);
xlabel(w_xLabelStr, 'fontsize',14);
line([w_min,w_max],[0,0], 'color','black');
set(gca,'xtick',w_x_tick);
set(gca,'xticklabel', w_x_tick_label_cell );
subplot(2,2,3);
plot(w, Y_imag);title(['Im', title_str], 'fontsize',14);
grid on; xlim([w_min,w_max]);ylim([(min(Y_imag)-0.5),(max(Y_imag)+0.5)]);
xlabel(w_xLabelStr, 'fontsize',14);
line([w_min,w_max],[0,0], 'color','black');
set(gca,'xtick',w_x_tick);
set(gca,'xticklabel', w_x_tick_label_cell );
subplot(2,2,4);
plot(w, Y_abs);title(['Mod', title_str], 'fontsize',14);
grid on; xlim([w_min,w_max]);ylim([(min(Y_abs)-0.5),(max(Y_abs)+0.5)]);
xlabel(w_xLabelStr, 'fontsize',14);
line([w_min,w_max],[0,0], 'color','black');
set(gca,'xtick',w_x_tick);
set(gca,'xticklabel', w_x_tick_label_cell );
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function tick_str = get_tick_str(num_val, denorm_val, unit_str)
num_val = round(num_val*1000);
denorm_val = round(denorm_val*1000);
gcd_n_d = gcd(num_val, denorm_val);
num_val = num_val/gcd_n_d;
denorm_val = denorm_val/gcd_n_d;
if(num_val == 0)
tick_str = ['0'];
else
if (denorm_val == 1)
denorm_str = unit_str;
else
denorm_str = [unit_str, '/', num2str(denorm_val)];
end
if(num_val == 1)
num_str = [];
elseif (num_val == -1)
num_str = ['-'];
else
num_str = num2str(num_val);
end
tick_str = [num_str, denorm_str];
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function ver_num = get_matlab_version()
ver_str_all = version; % such as 7.5.0.342 (R2007b)
ver_str = [ver_str_all(1), ver_str_all(2),ver_str_all(3)]; % such as 7.5
ver_num = str2num(ver_str);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function w_x_tick = get_w_x_tick_vec(w_min, w_max, w_x_tick_delta)
if(w_min < 0)
w_x_tick_R = [0:w_x_tick_delta: w_max];
temp = [w_x_tick_delta:w_x_tick_delta:-w_min];
w_x_tick_L = fliplr(-temp);
w_x_tick = [w_x_tick_L, w_x_tick_R];
else
w_x_tick = [w_min:w_x_tick_delta:w_max];
end
if(w_x_tick(1) > w_min)
w_x_tick = [w_min, w_x_tick];
end
if(w_x_tick(length(w_x_tick)) < w_max)
w_x_tick = [w_x_tick, w_max];
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function w_x_tick_label_cell = get_w_x_tick_label_cell(w_x_tick, w_x_tick_delta)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
N_w_x_tick = length(w_x_tick);
w_x_tick_label_cell = cell(N_w_x_tick,1);
ver_num = get_matlab_version();
if(ver_num >= 8.4)
tick_unit_str = '\pi';
else
tick_unit_str = 'pi';
end
for(idx = 1:N_w_x_tick)
num_val = w_x_tick(idx)/w_x_tick_delta ;
denorm_val = pi/w_x_tick_delta ;
tick_str = get_tick_str(num_val, denorm_val, tick_unit_str);
w_x_tick_label_cell{idx} = tick_str;
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%子函式2：
% file: .func_calc_dtft.m
% test with Matlab 2007
% Y(w) = DTFT(x[n]);
function Y = func_calc_dtft(x, n, w)
N = length(n);
N_w = length(w);
Y = zeros(N_w,1);
for idx = 1:N_w
e_jw = exp(-j*w(idx)*n);
Y(idx) = sum(e_jw .* x);
end–rec_dtft_plot.m 呼叫 func_calc_dtft.m 計算序列 的 DTFT( ω )
–rec_dtft_plot.m 呼叫 func_plot_dtft.m 繪製 曲線， 包括：序列的時域圖、 DTFT( ω ) 的實部、虛部、模值 曲線。
rec_dtft_plot.m 程式碼 模擬配置引數
w_min ：頻域變數左邊界
w_delta ：頻域變數計算精度
n_min ：時域序列左邊界
n_max ：時域序列右邊界
func_plot_dtft.m 程式碼模擬配置引數
w_x_tick_delta：繪圖水平柵格單位長度
模擬圖：
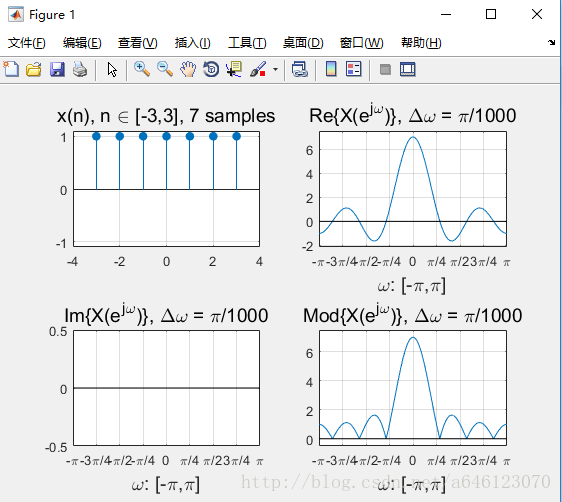
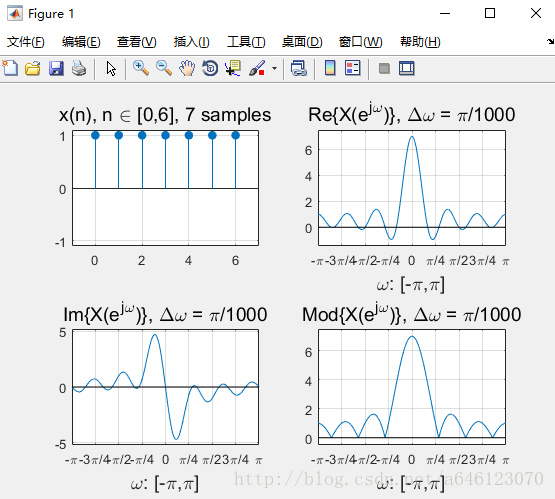
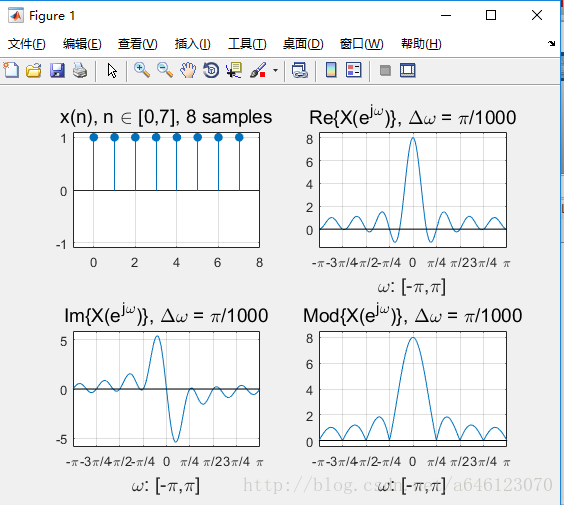
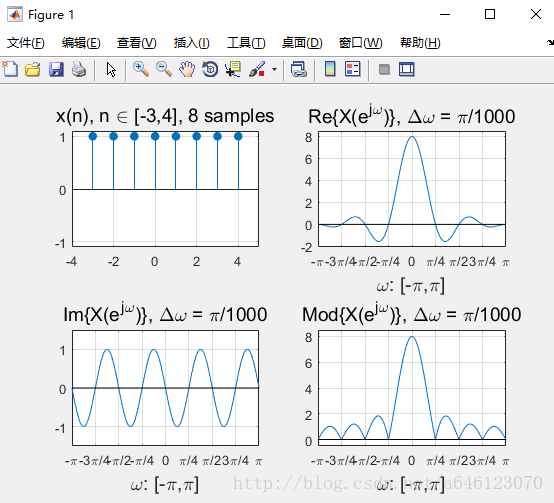
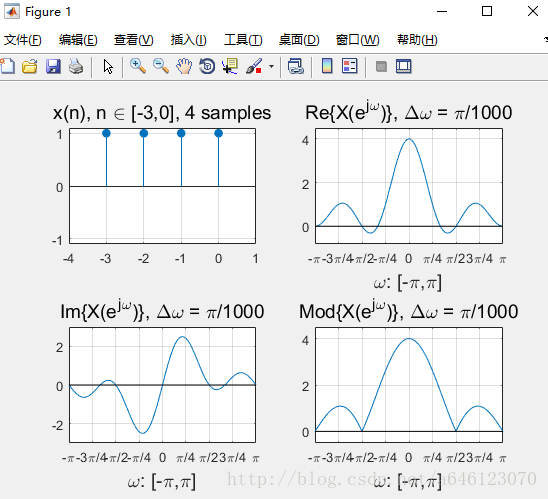
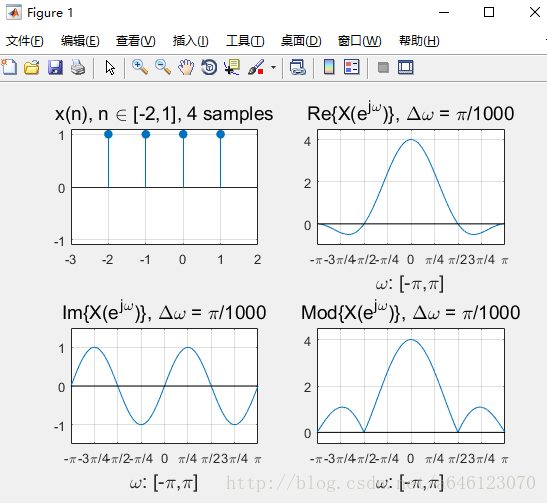
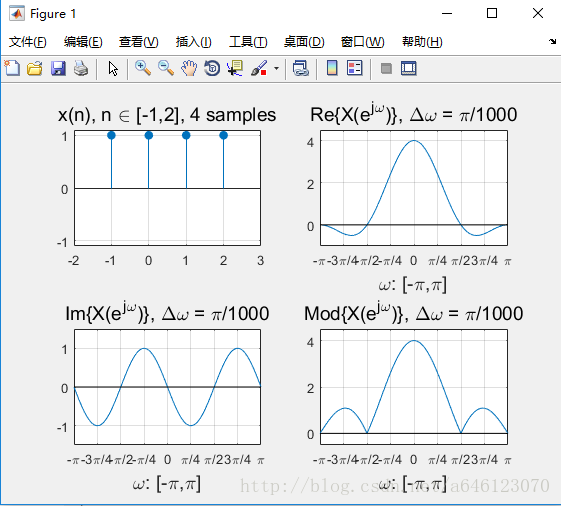
完成上機實驗後，回答以下問題
• 對於N點的矩形窗序列
– 其時域的相位變化（即序列最左邊和最右邊的位置）對DTFT變換的模值有影響麼？
相位變化越多，模值的主瓣越窄，旁瓣越多。
– 其時域的相位變化對DTFT變換的實部、虛部有影響麼？
相位變化越多，解析度越高
– 把序列按照縱軸翻轉，DTFT變換的結果發生什麼變化呢？
虛部變為相反數，實部及模值不變
– DTFT變換的模值曲線有幾個0點（0值柵格頻率）？有幾個峰值點？各自的位置和N的關係是什麼？（用公式表達）
N個取樣點，如果N為偶數則有N個0點，如果N為奇數則有N-1個0點。
有一個峰值點
– DTFT變換的模值曲線特徵（需要推導一下公式）
• 主瓣和旁瓣、以及各次旁瓣之間，寬度關係是什麼？
• 主瓣和旁瓣、以及各次旁瓣之間，高度關係是什麼？
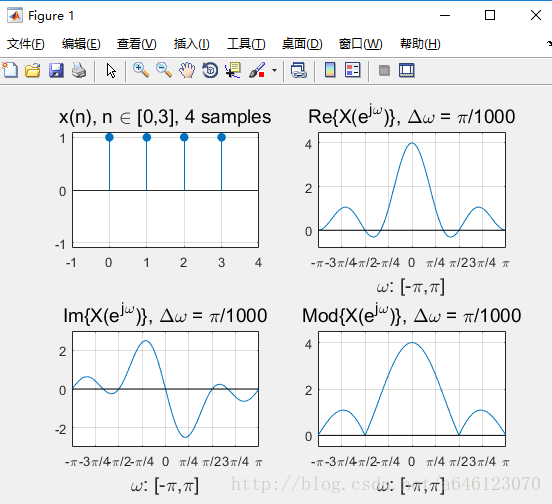
• 任務4、有限長正弦序列的DTFT
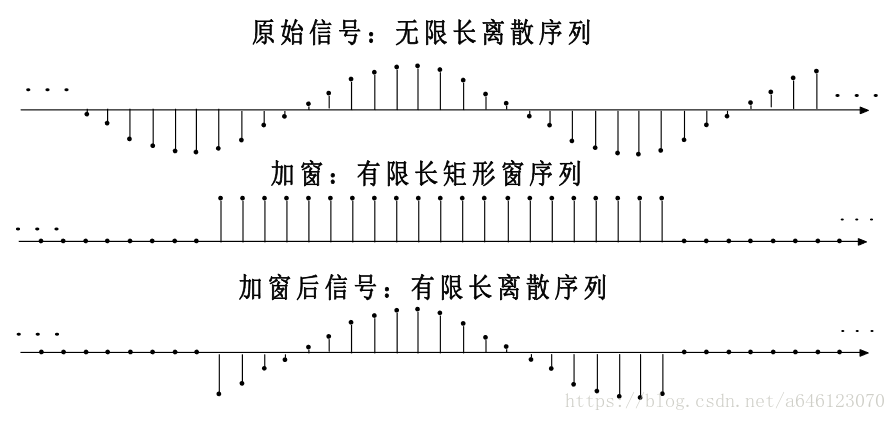
背景知識：有限長序列和矩形窗
• 有限長序列等效為： – 概念上的原始無限長序列，再乘以有限長的矩形窗之後得到
背景知識：頻域卷積定理
背景知識：有限長正弦序列的DTFT變換
實驗程式碼：
主函式
% file: plot_dtft.m
% test with Matlab 2007
clc
clear
close all
fig_fname = 'plot_dtft.png';
w_min = -1*pi;
w_max = 1*pi;
w_delta = pi/1000;
n_min = 0;
n_max = 7;
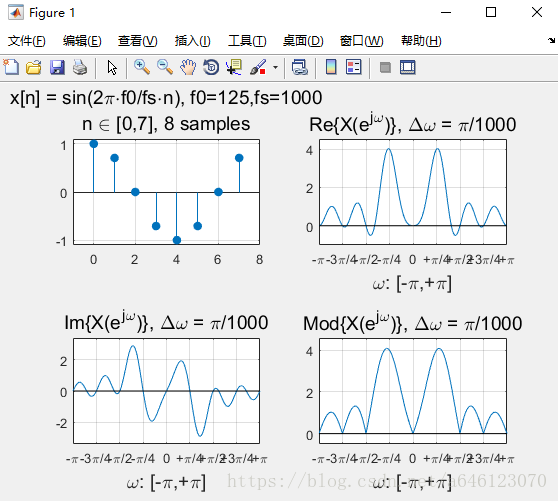
f0 = 125;
fs = 1000;
n = [n_min:1:n_max];
w = [w_min:w_delta:w_max];
N = length(n);
x = cos( 2*pi*f0/fs*n);
Y = func_calc_dtft(x, n, w);
x_dscp_str = ['x[n] = sin(2\pi\cdotf0/fs\cdotn), f0=', num2str(f0),',fs=' num2str(fs)];
h = func_plot_dtft(x,n,w,Y, x_dscp_str);子函式1：
% file: func_plot_dtft.m
% test with Matlab 2007, 2014
% Y[w] = DTFT(x[n]);
% plot time sequence x[n], real/imag part of Y[w], abs of Y[w]
function h = func_plot_dtft(x,n,w,Y, x_dscp_str);
h = figure;
N = length(n);
n_min = min(n);
n_max = max(n);
w_min = min(w);
w_max = max(w);
N_w = length(w);
w_delta = (w_max-w_min)/(N_w-1);
w_x_tick_delta = 1*pi/4 ;
w_x_tick = get_w_x_tick_vec(w_min, w_max, w_x_tick_delta);
w_x_tick_label_cell = get_w_x_tick_label_cell(w_x_tick, w_x_tick_delta);
ver_num = get_matlab_version();
if(ver_num >= 8.4)
if(length(w_x_tick_label_cell) >= 12)
x_tick_rot_angle = 270;
else
x_tick_rot_angle = 0;
end
end
Y_real = real(Y); Y_imag = imag(Y); Y_abs = abs(Y);
subplot(2,2,1);
title_str = {x_dscp_str; ['n \in [',int2str(n_min),',', int2str(n_max), ...
'], ', int2str(N), ' samples']};
stem(n, x, 'fill'); title(title_str, 'fontsize',14);
y_lim_max = 1.1*max(abs(x)); y_lim_min = -y_lim_max;
grid on; xlim([n_min-1,n_max+1]); ylim([y_lim_min, y_lim_max]);
subplot(2,2,2);
Left_str = get_tick_str((w_min/pi),1,'\pi');
Right_str = get_tick_str((w_max/pi),1,'\pi');
w_xLabelStr =['\omega: [', Left_str,',', Right_str, ']'];
title_str = ['\{X(e^{j\omega})\}, \Delta\omega = \pi/', num2str(pi/w_delta)];
plot(w, Y_real);title(['Re', title_str], 'fontsize',14);
grid on; xlim([w_min,w_max]);ylim([(min(Y_real)-0.5),(max(Y_real)+0.5)]);
xlabel(w_xLabelStr, 'fontsize',14);
line([w_min,w_max],[0,0], 'color','black');
set(gca,'xtick',w_x_tick);
set(gca,'xticklabel', w_x_tick_label_cell );
if(ver_num >= 8.4) set(gca,'XTickLabelRotation',x_tick_rot_angle); end
subplot(2,2,3);
plot(w, Y_imag);title(['Im', title_str], 'fontsize',14);
grid on; xlim([w_min,w_max]);ylim([(min(Y_imag)-0.5),(max(Y_imag)+0.5)]);
xlabel(w_xLabelStr, 'fontsize',14);
line([w_min,w_max],[0,0], 'color','black');
set(gca,'xtick',w_x_tick);
set(gca,'xticklabel', w_x_tick_label_cell );
if(ver_num >= 8.4) set(gca,'XTickLabelRotation',x_tick_rot_angle); end
subplot(2,2,4);
plot(w, Y_abs);title(['Mod', title_str], 'fontsize',14);
grid on; xlim([w_min,w_max]);ylim([(min(Y_abs)-0.5),(max(Y_abs)+0.5)]);
xlabel(w_xLabelStr, 'fontsize',14);
line([w_min,w_max],[0,0], 'color','black');
set(gca,'xtick',w_x_tick);
set(gca,'xticklabel', w_x_tick_label_cell );
if(ver_num >= 8.4) set(gca,'XTickLabelRotation',x_tick_rot_angle); end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function tick_str = get_tick_str(num_val, denorm_val, unit_str)
num_val = round(num_val*1000);
denorm_val = round(denorm_val*1000);
gcd_n_d = gcd(num_val, denorm_val);
num_val = num_val/gcd_n_d;
denorm_val = denorm_val/gcd_n_d;
if(num_val == 0)
tick_str = ['0'];
else
if (denorm_val == 1)
denorm_str = unit_str;
else
denorm_str = [unit_str, '/', num2str(denorm_val)];
end
if(num_val == 1)
num_str = [];
elseif (num_val == -1)
num_str = ['-'];
else
num_str = num2str(num_val);
end
if (num_val > 0)
num_str = ['+',num_str];
end
tick_str = [num_str, denorm_str];
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function ver_num = get_matlab_version()
ver_str_all = version; % such as 7.5.0.342 (R2007b)
ver_str = [ver_str_all(1), ver_str_all(2),ver_str_all(3)]; % such as 7.5
ver_num = str2num(ver_str);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function w_x_tick = get_w_x_tick_vec(w_min, w_max, w_x_tick_delta)
if(w_min < 0)
w_x_tick_R = [0:w_x_tick_delta: w_max];
temp = [w_x_tick_delta:w_x_tick_delta:-w_min];
w_x_tick_L = fliplr(-temp);
w_x_tick = [w_x_tick_L, w_x_tick_R];
else
w_x_tick = [w_min:w_x_tick_delta:w_max];
end
if(w_x_tick(1) > w_min)
w_x_tick = [w_min, w_x_tick];
end
if(w_x_tick(length(w_x_tick)) < w_max)
w_x_tick = [w_x_tick, w_max];
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function w_x_tick_label_cell = get_w_x_tick_label_cell(w_x_tick, w_x_tick_delta)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
N_w_x_tick = length(w_x_tick);
w_x_tick_label_cell = cell(N_w_x_tick,1);
ver_num = get_matlab_version();
if(ver_num >= 8.4)
tick_unit_str = '\pi';
else
tick_unit_str = 'pi';
end
for(idx = 1:N_w_x_tick)
num_val = w_x_tick(idx)/w_x_tick_delta ;
denorm_val = pi/w_x_tick_delta ;
tick_str = get_tick_str(num_val, denorm_val, tick_unit_str);
w_x_tick_label_cell{idx} = tick_str;
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%子函式2：
% file: .func_calc_dtft.m
% test with Matlab 2007
% Y(w) = DTFT(x[n]);
function Y = func_calc_dtft(x, n, w)
N = length(n);
N_w = length(w);
Y = zeros(N_w,1);
for idx = 1:N_w
e_jw = exp(-j*w(idx)*n);
Y(idx) = sum(e_jw .* x);
endsin_dtft_plot.m 程式碼 模擬配置引數
w_min ：頻域變數左邊界
w_max ：頻域變數右邊界
w_delta：頻域變數計算精度
n_min ：時域序列左邊界
n_max ：時域序列右邊界
f0 ：正弦訊號頻率
fs ：正弦訊號取樣率
func_plot_dtft.m 程式碼 模擬配置引數
w_x_tick_delta ： 繪圖水平柵格單位長
實驗結果：
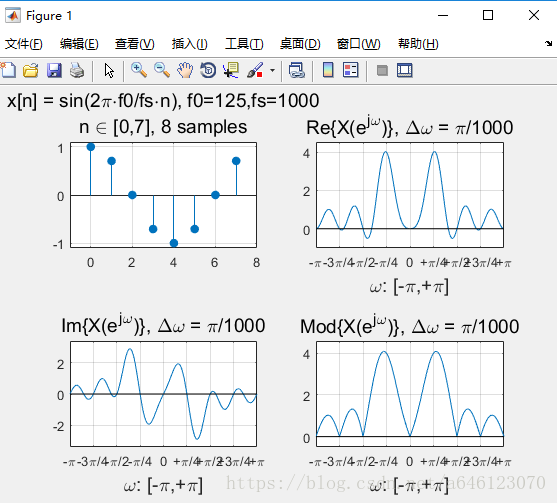
修改實驗引數，可以得到以下結果：
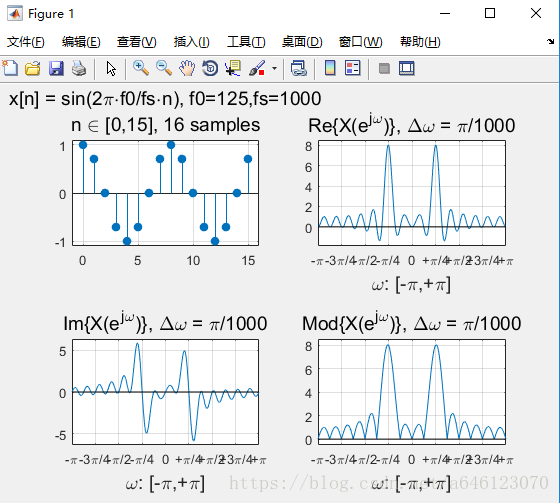
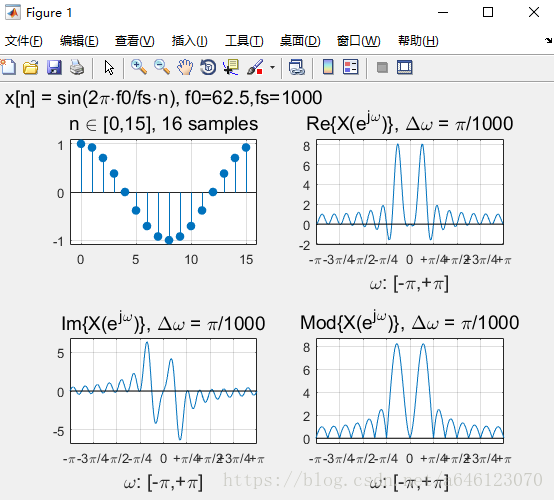
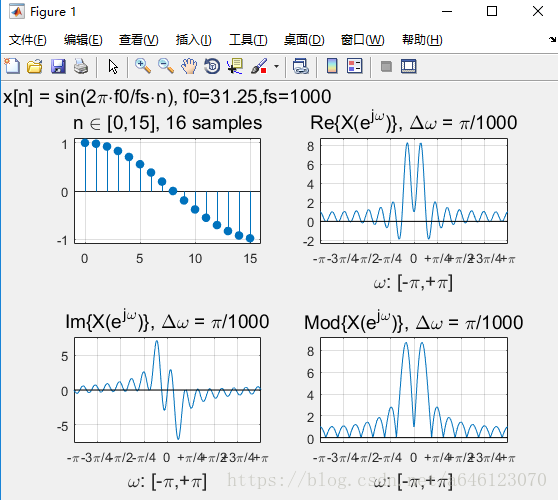
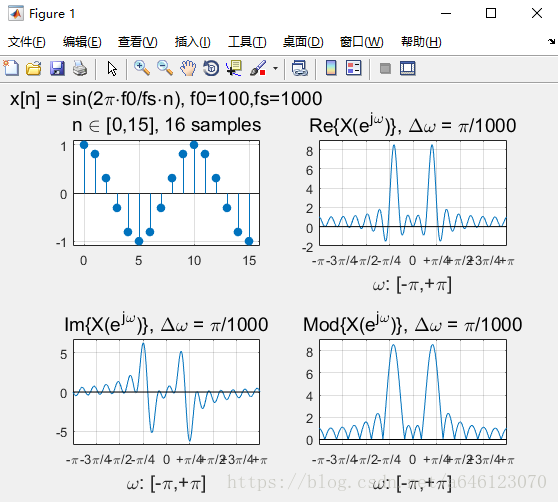
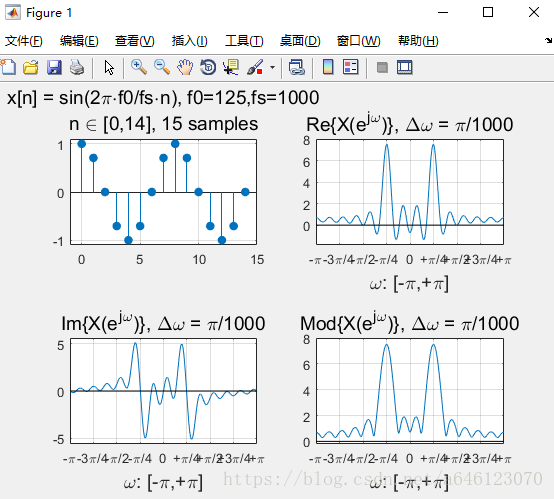
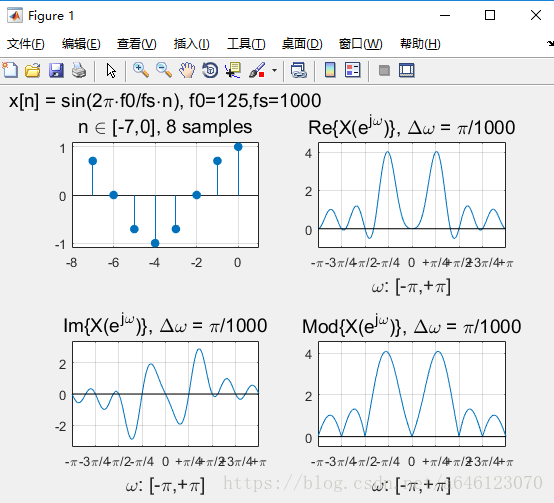
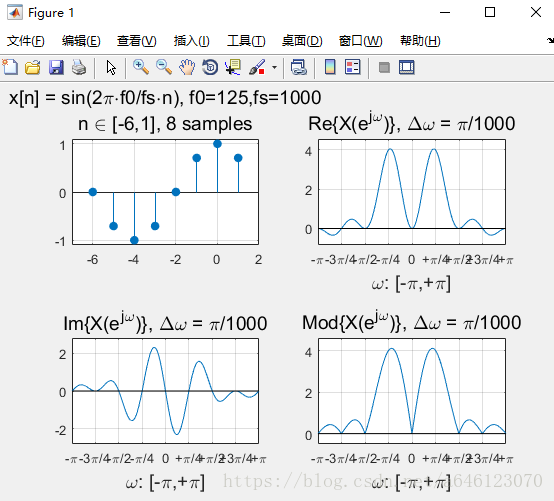
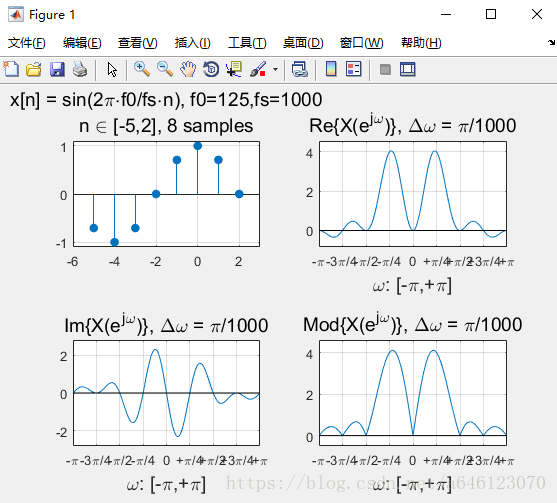
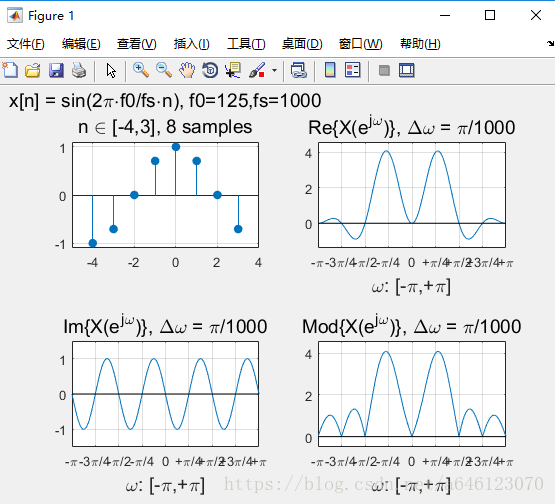
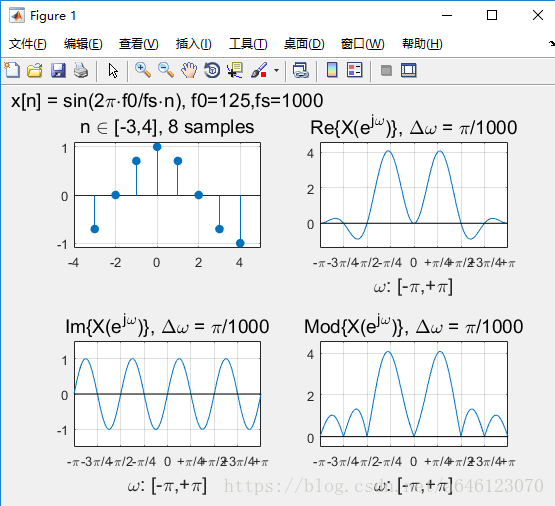
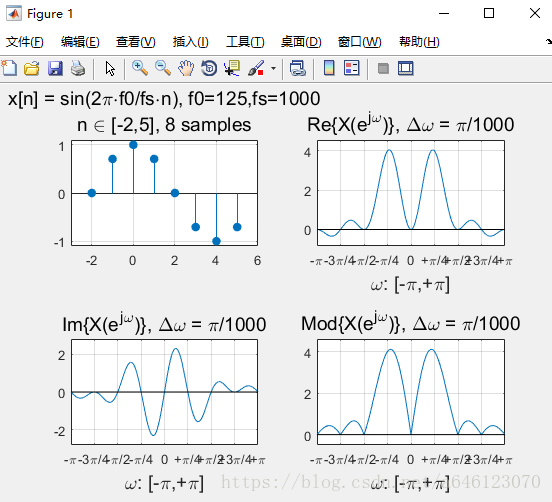
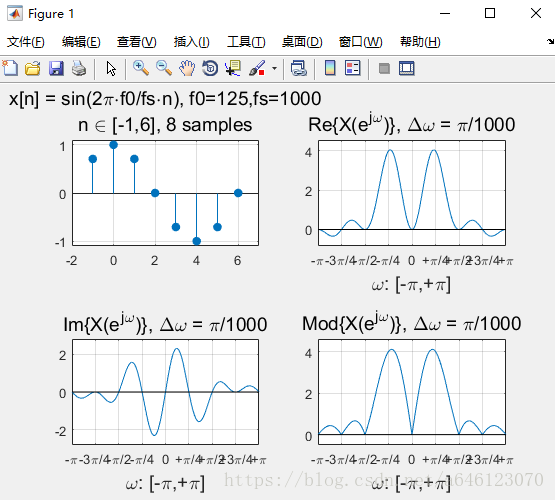
• 回答以下問題
• 對於實數序列訊號，其DTFT變換的對稱性如何？ – 請按照實部、虛部、模值分別回答
實部、模值是偶對稱，虛部是奇對稱。
• 正弦序列的DTFT曲線峰值，一定出現在訊號歸一化數字角頻率的位置麼？為什麼會這樣？
不一定，
• 從實驗中可以看到，對於單音正弦訊號，頻率過低時在DTFT 曲線上將無法分辨出正負頻率的峰值。請嘗試分析一下原因
• 假定正弦訊號序列不變，擷取不同的有限長相位區間構成不 同的有限長序列，然後進行DTFT分析 – 請問序列相位對DTFT變換有什麼影響？ – 請嘗試分別從實部、虛部、模值的角度分析
模值不變，只是影響實部、虛部的各位置的數值大小。
• 任務5、 DTFT 和 DFT 關係探尋
DFT等於DTFT的取樣
DTFT 定義式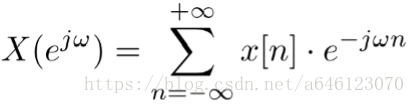 
DFT 定義式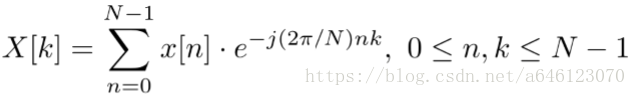 
若 x[n] 是一個在[0,N − 1]區間內有非零值的有限長序列， 且，令：ω(k) = 2π·k/N, 0 ≤ k ≤ N − 1，則在ω(k) 的位置上 DFT 和 DTFT 等價。
以上結論說明，DFT是在0 ~ 2π 區間上對 DTFT 的等間隔 取樣，取樣間隔大小為： 2π/N
實驗程式碼：
• sin_dtft_dft_plot.m ：主程式
• func_plot_dtft_dft.m：繪圖DTFT和DFT的函式
• 注意：如果要同時顯示DFT和DTFT結果需要如下設定 – w_min = 0; w_max = 2*pi;
主函式：
% file: sin_dtft_dft_plot.m
% test with Matlab 2007,2014
clc
clear
close all
fig_fname = 'plot_dtft.png';
% to plot DFT with DTFT, must set w range as [0,2pi]
w_min = 0;
w_max = 2*pi;
w_delta = pi/1000;
n_min = 0;
n_max = 16-1;
f0 = 10;
fs = 100;
n = [n_min:1:n_max];
w = [w_min:w_delta:w_max];
N = length(n);
x = sin(2*pi*f0/fs*n);
Y = func_calc_dtft(x, n, w);
Y_DFT = fft(x);
x_dscp_str = ['x[n] = sin(2\pi\cdotf0/fs\cdotn), f0=', num2str(f0),',fs=' num2str(fs)];
h = func_plot_dtft_dft(x,n,w,Y,Y_DFT, fs, x_dscp_str);子函式1：
% file: func_calc_dtft.m
% test with Matlab 2007
% Y(w) = DTFT(x[n]);
function Y = func_calc_dtft(x, n, w)
N = length(n);
N_w = length(w);
Y = zeros(N_w,1);
for idx = 1:N_w
e_jw = exp(-j*w(idx)*n);
Y(idx) = sum(e_jw .* x);
end
子函式2:
% file: func_plot_dtft_dft.m
% test with Matlab 2007, 2014
% Y[w] = DTFT(x[n]);
% plot time sequence x[n], real/imag part of Y[w], abs of Y[w]
function h = func_plot_dtft_dft(x,n,w,Y, Y_DFT, fs, x_dscp_str);
h = figure;
N = length(n);
n_min = min(n);
n_max = max(n);
w_min = min(w);
w_max = max(w);
if(w_min ~= 0 ) disp('WARNING, to plot DFT with DTFT w_min must be 0'); end
if(w_max ~= 2*pi) disp('WARNING, to plot DFT with DTFT w_max must be 2*pi'); end
N_w = length(w);
w_delta = (w_max-w_min)/(N_w-1);
w_x_tick_delta = 2*pi/16 ;
w_x_tick = get_w_x_tick_vec(w_min, w_max, w_x_tick_delta);
w_x_tick_label_cell = get_w_x_tick_label_cell(w_x_tick, w_x_tick_delta);
ver_num = get_matlab_version();
if(ver_num >= 8.4)
if(length(w_x_tick_label_cell) >= 12)
x_tick_rot_angle = 270;
else
x_tick_rot_angle = 0;
end
end
Y_real = real(Y); Y_imag = imag(Y); Y_abs = abs(Y);
N_DFT = length(Y_DFT);
w_DFT = n*2*pi/N;
Y_DFT_real = real(Y_DFT); Y_DFT_imag = imag(Y_DFT); Y_DFT_abs = abs(Y_DFT);
subplot(2,2,1);
title_str = {x_dscp_str; ['n \in [',int2str(n_min),',', int2str(n_max), ...
'], ', int2str(N), ' samples']};
stem(n, x, 'fill'); title(title_str, 'fontsize',14);
y_lim_max = 1.1*max(abs(x)); y_lim_min = -y_lim_max;
grid on; xlim([n_min-1,n_max+1]); ylim([y_lim_min, y_lim_max]);
subplot(2,2,2);
Left_str = get_tick_str((w_min/pi),1,'\pi');
Right_str = get_tick_str((w_max/pi),1,'\pi');
w_xLabelStr =['\omega: [', Left_str,',', Right_str, ']'];
title_str = ['\{X(e^{j\omega})\}, \Delta\omega = \pi/', num2str(pi/w_delta)];
plot(w, Y_real);title(['Re', title_str], 'fontsize',14);
grid on; xlim([w_min,w_max]);ylim([(min(Y_real)-0.5),(max(