POJ1456:Supermarket(並查集+貪心)
Supermarket
| Time Limit: 2000MS | Memory Limit: 65536K | |
| Total Submissions: 17634 | Accepted: 7920 |
題目連結:http://poj.org/problem?id=1456
Description:
A supermarket has a set Prod of products on sale. It earns a profit px for each product x∈Prod sold by a deadline dx that is measured as an integral number of time units starting from the moment the sale begins. Each product takes precisely one unit of time for being sold. A selling schedule is an ordered subset of products Sell ≤ Prod such that the selling of each product x∈Sell, according to the ordering of Sell, completes before the deadline dx or just when dx expires. The profit of the selling schedule is Profit(Sell)=Σx∈Sell
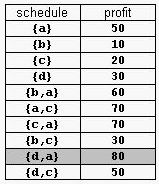
For example, consider the products Prod={a,b,c,d} with (pa,da)=(50,2), (pb,db)=(10,1), (pc,dc)=(20,2), and (pd,dd)=(30,1). The possible selling schedules are listed in table 1. For instance, the schedule Sell={d,a} shows that the selling of product d starts at time 0 and ends at time 1, while the selling of product a starts at time 1 and ends at time 2. Each of these products is sold by its deadline. Sell is the optimal schedule and its profit is 80.
Write a program that reads sets of products from an input text file and computes the profit of an optimal selling schedule for each set of products.
Input:
A set of products starts with an integer 0 <= n <= 10000, which is the number of products in the set, and continues with n pairs pi di of integers, 1 <= pi <= 10000 and 1 <= di <= 10000, that designate the profit and the selling deadline of the i-th product. White spaces can occur freely in input. Input data terminate with an end of file and are guaranteed correct.
Output:
For each set of products, the program prints on the standard output the profit of an optimal selling schedule for the set. Each result is printed from the beginning of a separate line.
Sample Input:
4 50 2 10 1 20 2 30 1
7 20 1 2 1 10 3 100 2 8 2
5 20 50 10
Sample Output:
80
185
題意:
給出n個商品以及它們的利潤和截至日期,每天只能賣出一個商品,截止日期過後就不能出售了,問最大利潤是多少。
題解:
第一反應肯定是採用貪心的策略,選擇一個最大利潤的出售,但是因為這裡有個日期,這裡的貪心不一定可以得到最後的最大利潤。
所以我們也應該考慮日期,發現當出售商品在其截至日期時,是最優的,因為這將不會影響之前商品的出售。
這裡的貪心我們可以採用優先佇列對其進行優化,並且日期要倒過來列舉(結合貪心策略想想)。
這裡我用的是並查集對其進行優化,商品出售的時間儘可能得接近其截至日期,如果在那天商品出售了,又有另外一個商品在那天出售,那麼我們就挪到前一天進行出售。
我們就用並查集維護離截止日期最近的空閒時間,查詢速度挺快的。
程式碼如下:
#include <cstdio> #include <cstring> #include <algorithm> #include <iostream> using namespace std; const int N = 10005; int f[N]; int n; struct node{ int p,d; bool operator < (const node &A)const{ return A.p<p; } }a[N]; int find(int x){return f[x]==x ? f[x] : f[x]=find(f[x]);} int main(){ while(~scanf("%d",&n)){ for(int i=1;i<=10000;i++) f[i]=i; for(int i=1;i<=n;i++) scanf("%d%d",&a[i].p,&a[i].d); sort(a+1,a+n+1); int ans = 0; for(int i=1;i<=n;i++){ int fd = find(a[i].d); if(fd>0){//存在空閒時間 ans+=a[i].p; f[fd]=fd-1; } } printf("%d\n",ans); } return 0; }
