參考 ： https://www.scratchapixel.com/lessons/mathematics-physics-for-computer-graphics/monte-carlo-methods-mathematical-foundations

Mean And Expected Value 

Again, note that the mean and the expected value are equal however the mean is a simple average of numbers not weighted

by anything, while the expected value is a sum of numbers weighted by their probability. We can write:

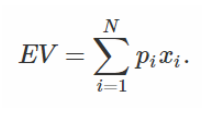
Where EV stands for expected value, and pi is the probability associated with outcome xi.

Let's now formalize this concept. The mean of a population(總體) parameter is denoted with the greek letter μ (read "mu"). In

our card example, you can compute this value in two ways. You can either add up all the numbers on the cards of all the cards

and divide the resulting number by the total number of cards, or if you know the cards probability distribution (let's say we do

have this information) then you can use the method described above: you multiply each outcome by its own probability and

add up the numbers. Let's write these two solutions and check they give the same result:

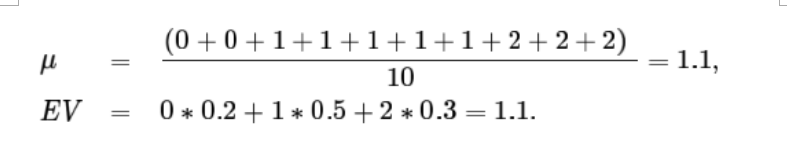
（Mean 和 Expected Value 其實得到的結果是一致的，但是計算方法不一樣，Expected Value 簡單理解就是概率分佈和輸出結果的加權平均）

Sample Mean

Each time we add a new observation and compute the mean of our random variable, using all the observations collected so

far(到目前為止), the value of the mean changes. However what you will eventually(最後) observe(觀察), is that at some point,

you will have so many observations, that adding one more observation to the computation of the mean is going to have less

and less of an effect(越來越少的影響) on the resulting value. Another way of looking at it, is to say that the mean of the random

variables converges to( 收斂) a singular(單一) value as the sample size increases, and if you haven't guessed(猜想) yet, this

value is the same as the expected value (and if you haven't guessed, we will explain it soon). This is generally easy to

intuitively understand. If you have a thousand people whose height is between say 165 and 175 cm (and you have an average

height of 170 cm so far) then having one individual whose height is very different from most people's height in your sample, is

unlikely to have a great impact(影響) on the overall average height of that sample. You can see this as a dilution(稀釋) process.

Adding a drop of(一滴) milk to a one litre of(一公升) pure water is unlikely to make the water look cloudy(渾濁).

Because everything in statistics has a name (and a precise(精確) meaning) the mean of a collection of observations(觀察

值) produced by a random variable X, is called a sample mean (remember that a collection of observations is called a sample or a statistics). Sample mean is generally denoted 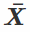 which you can read "X bar", and mathematically we can express it as:

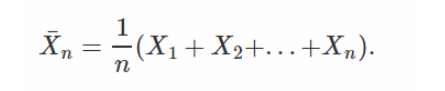
Where X1,X2X1,X2, ... is a sequence of random variables which have the property to be independent and identically

distributed (or i.i.d).

In summary, our C++ program shows that as the sample size increases, the sample mean converges to the expected value:

Where the symbol ≈ means "approximation" (but it would be better in our context to take the habit of(習慣) using the word

estimation(估計) instead and we will soon explain why). The idea that the sample mean converges in value and probability to

the expected value as the sample size increases( sample mean 收斂於一個值，這個值隨著樣本數的增加，這個值越來越可能

是expected value), is expressed(表達) in a theorem from probability theory known as the Law of Large Numbers (大數定律)

(or LLN). They are a few possible approaches (幾種方法)to explaining(解釋) the theorem(定理); one way is to consider than

as(一種方法是考慮) the number of trials(嘗試) becomes large, the relative frequency(相對的頻率) of each outcome from the

experiment tends to(傾向於) approach(靠近) the probability of that outcome(輸出的概率).

In other words, as we keep increasing the number of trials, the theorem tells us that the average of a discrete random variable

tends to approach a limit which is the random variable expected value (see the grey box above for mode details on this):

The superscript(下標) p over the right arrow, means "converges in probability(收斂的概率)". You can also define this property

as:

In words, it means that the probability that the difference(差異)  between the sample mean and the population mean is smaller

than a very very small value (here denoted by the greek symbol epsilon ϵ) is 1 as n approaches infinity. We generally speak

of convergence in probability. In conclusion(最後), you should remember that the sample mean 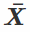 of a random sample

always converge in probability to the population mean μ of the population from which the random sample was taken.

（sample mean 只是進行 取樣值 的 平均，而且 隨著樣本數的增加，sample mean 會越來越靠近 expected value）