Uniformly Sampling A Hemisphere

1. Vector UniformSampleHemisphere(float u1, float u2);

Vector UniformSampleHemisphere(float u1, float u2) {
    float z = u1;
    float r = sqrtf(max(0.f, 1.f - z*z));
    float phi = 2 * M_PI * u2;
    float x = r * cosf(phi);
    float y = r * sinf(phi);
    return Vector(x, y, z);
}
 

作用：

（傳入u1，u2，範圍都是[0，1]，均勻地選擇半球上的一個方向，具體的數學原來可以參考《PBRT》P663，這裡就不抄出來）

choosing a direction on the hemisphere uniformly with respect to solid angle. 

2. float  UniformHemispherePdf();

float UniformHemispherePdf() {
    return INV_TWOPI;
}

作用：

（取樣半球方向的pdf）

For hemispheres (and all other directional sampling), these functions return
values with respect to solid angle. For the hemisphere, the solid angle PDF is a constant
p(ω) = 1/(2π).

Uniformly Sampling Full Sphere

1. Vector UniformSampleSphere(float u1, float u2);

Vector UniformSampleSphere(float u1, float u2) {
    float z = 1.f - 2.f * u1;
    float r = sqrtf(max(0.f, 1.f - z*z));
    float phi = 2.f * M_PI * u2;
    float x = r * cosf(phi);
    float y = r * sinf(phi);
    return Vector(x, y, z);
}
 

作用：

（傳入u1，u2，範圍都是[0，1]，均勻地選擇整一個球上的一個方向）

Sampling the full sphere uniformly over its area follows almost exactly the same derivation,
which we omit here.

2. float  UniformSpherePdf();

float UniformSpherePdf() {
    return 1.f / (4.f * M_PI);
}

作用：

（取樣整一個球方向的pdf）

Uniformly Sampling Disk

(a) When the obvious but incorrect mapping of uniform random variables to points on
the disk is used, the resulting distribution is not uniform and the samples are more likely to be near
the center of the disk. (b) The correct mapping gives a uniform distribution of points.

1. void UniformSampleDisk(float u1, float u2, float *x, float *y);

void UniformSampleDisk(float u1, float u2, float *x, float *y) {
    float r = sqrtf(u1);
    float theta = 2.0f * M_PI * u2;
    *x = r * cosf(theta);
    *y = r * sinf(theta);
}

作用：

（上圖的a，不能均勻取樣一個圓盤）

2. void ConcentricSampleDisk(float u1, float u2, float *dx, float *dy);

void ConcentricSampleDisk(float u1, float u2, float *dx, float *dy) {
    float r, theta;
    // Map uniform random numbers to $[-1,1]^2$
    float sx = 2 * u1 - 1;
    float sy = 2 * u2 - 1;

    // Map square to $(r,\theta)$

    // Handle degeneracy at the origin
    if (sx == 0.0 && sy == 0.0) {
        *dx = 0.0;
        *dy = 0.0;
        return;
    }
    if (sx >= -sy) {
        if (sx > sy) {
            // Handle first region of disk
            r = sx;
            if (sy > 0.0) theta = sy/r;
            else          theta = 8.0f + sy/r;
        }
        else {
            // Handle second region of disk
            r = sy;
            theta = 2.0f - sx/r;
        }
    }
    else {
        if (sx <= sy) {
            // Handle third region of disk
            r = -sx;
            theta = 4.0f - sy/r;
        }
        else {
            // Handle fourth region of disk
            r = -sy;
            theta = 6.0f + sx/r;
        }
    }
    theta *= M_PI / 4.f;
    *dx = r * cosf(theta);
    *dy = r * sinf(theta);
}

作用：

（上圖的b，均勻取樣一個圓盤）

Cosine-Weighted-Hemisphere Sampling

1. Vector CosineSampleHemisphere(float u1, float u2)

inline Vector CosineSampleHemisphere(float u1, float u2) {
    Vector ret;
    ConcentricSampleDisk(u1, u2, &ret.x, &ret.y);
    ret.z = sqrtf(max(0.f, 1.f - ret.x*ret.x - ret.y*ret.y));
    return ret;
}

inline float CosineHemispherePdf(float costheta, float phi) {
    return costheta * INV_PI;
}

作用：

（取樣一個半球的方向，得到的球頂部的方向的概率更加大，pdf 與 cos 成正比，這裡的函式的做法就是，x，y 的取樣就直接用 disk 的取樣，而z 的取樣就是 cos 的）

it is often useful to sample from a distribution
that has a shape similar to that of the integrand being estimated.For example, because
the scattering equation weights the product of the BSDF and the incident radiance with
a cosine term, it is useful to have a method that generates directions that are more likely
to be close to the top of the hemisphere, where the cosine term has a large value, than the
bottom, where the cosine term is small.

Mathematically, this means that we would like to sample directions ω from a PDF

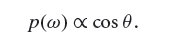
Sampling A Triangle

1. void UniformSampleTriangle(float ud1, float ud2, float *u, float *v);

void UniformSampleTriangle(float u1, float u2, float *u, float *v) {
    float su1 = sqrtf(u1);
    *u = 1.f - su1;
    *v = u2 * su1;
}

作用：

（均勻地取樣一個三角形）

Although uniformly sampling a triangle

Distribution2D

struct Distribution2D {
    // Distribution2D Public Methods
    Distribution2D(const float *data, int nu, int nv);
    ~Distribution2D();
    void SampleContinuous(float u0, float u1, float uv[2],
                          float *pdf) const {
        float pdfs[2];
        int v;
        uv[1] = pMarginal->SampleContinuous(u1, &pdfs[1], &v);
        uv[0] = pConditionalV[v]->SampleContinuous(u0, &pdfs[0]);
        *pdf = pdfs[0] * pdfs[1];
    }
    float Pdf(float u, float v) const {
        int iu = Clamp(Float2Int(u * pConditionalV[0]->count), 0,
                       pConditionalV[0]->count-1);
        int iv = Clamp(Float2Int(v * pMarginal->count), 0,
                       pMarginal->count-1);
        if (pConditionalV[iv]->funcInt * pMarginal->funcInt == 0.f) return 0.f;
        return (pConditionalV[iv]->func[iu] * pMarginal->func[iv]) /
               (pConditionalV[iv]->funcInt * pMarginal->funcInt);
    }
private:
    // Distribution2D Private Data
    vector<Distribution1D *> pConditionalV;
    Distribution1D *pMarginal;
};



Distribution2D::Distribution2D(const float *func, int nu, int nv) {
    pConditionalV.reserve(nv);
    for (int v = 0; v < nv; ++v) {
        // Compute conditional sampling distribution for $\tilde{v}$
        pConditionalV.push_back(new Distribution1D(&func[v*nu], nu));
    }
    // Compute marginal sampling distribution $p[\tilde{v}]$
    vector<float> marginalFunc;
    marginalFunc.reserve(nv);
    for (int v = 0; v < nv; ++v)
        marginalFunc.push_back(pConditionalV[v]->funcInt);
    pMarginal = new Distribution1D(&marginalFunc[0], nv);
}


Distribution2D::~Distribution2D() {
    delete pMarginal;
    for (uint32_t i = 0; i < pConditionalV.size(); ++i)
        delete pConditionalV[i];
}

作用：

（Distribution2D 利用 u,v,[0,1], 進行取樣一個離散2D分佈函式，例如 Texture, 內部主要的實現都是使用  Distribution1D）

Our final example will show how to sample from discrete 2D distributions. We will
consider the case of a 2D function defined over (u, v) ∈ [0, 1]2 by a 2D array of nu × nv
sample values. This case is particularly useful for generating samples from distributions
defined by texture maps and environment maps.