1 前言

作為一名OI選手，至今未寫過fft相關的部落格，真是一大遺憾，這也導致我並沒有真正推過fft的所有式子
這一篇fft的部落格我將詳細介紹多項式乘法，易於理解，主要是為了等我啥時候忘了回來看，當然，一些公式會有些枯燥，如果是初學者請耐心看完哦，還有，畢竟這是手寫出來的，如果有錯誤，歡迎指正！

2 介紹

本欄用來普及一些知識和對FFT的思路進行描述
多項式乘法，顧名思義，首先是講到多項式，那麼什麼是多項式呢？

2.1 多項式

首先是多項式的定義，想必大家都知道(你上過初中吧)，而在這裡，我們所說的多項式都是單個未知數x的
所以，在我們正常人眼中的一個次多項式就是形如 $f$

( x ) = a 0 x 0 + a 1 x 1 + ⋅ ⋅ ⋅ + a n − 1 x n − 1 f(x)=a_0x^0+a_1x^1+···+a_{n-1}x^{n-1}
沒錯，這就是大名鼎鼎的係數表示法
然後呢，由於在後面要用到，所以我在這裡再介紹一種點值表示法
就是將n個不同的值 $x_0,x_1···x_{n-1}$分別帶入 $f(x)$，獲得n個結果 $y_0,y_1···y_{n-1}$，這n對數 $(x_0,y_0),(x_1,y_1)···(x_{n-1},y_{n-1})$就可以表示出這個多項式
看到這裡，如果你是初學者，你一定會感到非常迷茫，這為什麼對呢？
看到這裡，如果你是個FFT高手，你可能會感到迷茫，這為什麼對呢？
（dalao勿噴）

這張圖片裡係數表示法相當於是最右側的那個矩陣
而點值表示法則包含了左邊的兩個矩陣，可以通過這兩個矩陣計算出最右側的那個矩陣，所以兩種表示法是等價的
撒花
注：另外要說的是，由於演算法需要，本部落格所說的n次多項式都預設n是2的冪次（如果不足可以新增0來補）

2.2多項式的乘法

在做了那麼久的各種數學題後，我對多項式乘法有了有了的理解
對於一個一般的給定係數表示法的多項式乘法問題
比如兩個n次多項式A(x),B(x)，給出係數表示法，求它們的乘積C(x)
分別列舉兩個多項式中的每一項，分別是 $O(n)的$，所以總複雜度為 $O(n^2)$
這是一個很方便的做法

你可以發現一件很有趣的事情，那就是如果給出的是點值表示法，並且兩個多項式的x分別對應相等，那麼把y對應相乘，就能 $O(n)$的獲取乘積的點值表示法

2.3 快速傅立葉變換（FFT）

那麼，FFT是用來幹什麼的呢？
對於一個多項式乘法問題，當給出係數表示法的時候， $O(n)$的複雜度有時候並不足夠優越，而FFT就是一個能使多項式乘法做到 $O（nlogn）$的一個演算法，具體的原理其實非常清晰

• 兩個多項式的係數表示法
  求值，O(nlogn)
• 兩個多項式的點值表示法
  點值乘法，O(n)
• 兩個多項式乘積的點值表示法
  插值，O(nlogn)
• 兩個多項式乘積的係數表示法

是不是一目瞭然呢？當然，要具體實現，還需要細細說來

3 實現

現在你已經大致知道FFT要幹什麼了，現在你已經會在點值情況下 $O(n)$進行多項式乘法，剩下的就是要解決兩個問題——求值與插值了

3.1 暴力演算法（ $O(n^3)$）

要先做題，必先暴力
首先是求值，加入你現在隨便找了n個互不相同的x，帶入其中，是什麼複雜度呢 $O(n^2)$的
然後是插值，有一個非常妙的方法，假設所有的a都是未知數，那麼這個問題就變成了經典的高斯消元問題，複雜度 $O(n^3)$
不好意思，這兩個操作的複雜度都光榮的在 $O(n^2)$以上，使得當前這個演算法的總複雜度為 $O(n^3)$，比文章開始的那個 $O（n^2）$都要差，不要灰心，既然複雜度不優，那就循序漸進的優化

3.2 離散傅立葉變換（通過優化使上面演算法複雜度降到 $O(n^2)$，請仔細看完，這是基礎）

你會發現，點值表示法有一個很好的特性，就是那個代入的x可以自己選擇
離散傅立葉變換的思路是將n個x的值取n個單位根（模長為一的複數）

複數（這是一個知識拓展框）

$\sqrt{-1}$這個數，在實數範圍內是不存在的，所以拓展出複數這一概念，設 $i=\sqrt{-1}$，複數就是能夠被表示為 $z=x+y*i$的數。所以對一個複數，可以用有序數對(x,y)表示，在座標軸上有對應的點，而這個複數就是從(0,0)到(x,y)的一條有向線段（只會向量的同學可以把它看成向量），而這個複數的模長就等於(0,0)到(x,y)的距離
由於複數是數，所以也有各種運算
加法：(a+bi)+(c+di)=(a+c)+(b+d)i
減法：(a+bi)-(c+di)=(a-c)+(b-d)i
乘法：(a+bi)*(c+di)=(ac-bd)+(ad+bc)i
當然，C++有專門的complex變數可以宣告，但是

不推薦使用！！！

為什麼呢？因為FFT本身就有一定的常數，如果再用系統complex常數會更大，所以推薦自己手寫struct

那麼什麼是單位根呢？

3.2.1 單位根

單位根所在的點是把單位圓（以原點為圓心，半徑為1的圓）從（0,1）開始平均分成n份的分割點
如下圖，這就是n=8時的單位圓，綠色圓上的紅點就是單位根所在的點

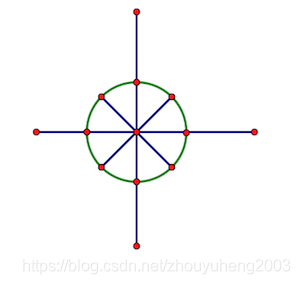
從(0,1)開始逆時針將這n個點編號，所表示的單位根分別為 $w_n^1,w_n^1···,w_n^{n-1}$，特殊的， $w_n^1$被稱為n次單位根。容易發現每個單位根都非常好算，即 $w_n^k=(cos\frac{k}{n} 2π,sin\frac{k}{n} 2π)$
這個用三角函式的想法非常好證
知道了這個之後，你會發現很多性質

性質1： $w_n^k=(w_n^1)^k$

證明：
$     w n k ∗ w n 1 = ( c o s k n 2 π , s i n k n 2 π ) ∗ ( c o s 1 n 2 π , s i n 1 n 2 π ) = ( c o s k n 2 π ∗ c o s 1 n 2 π − s i n k n 2 π ∗ s i n 1 n 2 π , s i n k n 2 π ∗ c o s 1 n 2 π + c o s k n 2 π ∗ s i n 1 n 2 π ) = ( c o s k + 1 n 2 π , s i n k + 1 n 相關推薦 洛谷P3803 【模板】多項式乘法（FFT） 【fft】 n+1 swap 提示 接下來 bug ret const define %d 題目 這是一道FFT模板題 輸入格式 給定一個n次多項式F(x)，和一個m次多項式G(x)。 請求出F(x)和G(x)的卷積。 輸出格式 第一行2個正整數n,m。 接下來一行n+1個數字，從低到 洛谷P3803 【模板】多項式乘法（FFT） git pen == lex def min problem main for 傳送門 FFT我啥都不會，先坑著 1 //minamoto 2 #include<iostream> 3 #include<cstdio> 4 多項式乘法（FFT） 1 前言 作為一名OI選手，至今未寫過fft相關的部落格，真是一大遺憾，這也導致我並沒有真正推過fft的所有式子 這一篇fft的部落格我將詳細介紹多項式乘法，易於理解，主要是為了等我啥時候忘了回來看，當然，一些公式會有些枯燥，如果是初學者請耐心看完哦，還有，畢竟這是手寫出來的，如果有 洛谷 3803 【模板】多項式乘法（FFT） 題目：https://www.luogu.org/problemnew/show/P3803 https://www.cnblogs.com/zwfymqz/p/8244902.html http://www.cnblogs.com/RabbitHu/p/FFT.html http://picks.lo 洛谷 P3803 多項式乘法（FFT） —— FFT 題目：https://www.luogu.org/problemnew/show/P3803 終於學了FFT了！ 參考部落格：https://www.cnblogs.com/zwfymqz/p/8244902.html http://www.cnblogs.com/RabbitHu/p/FFT.html 洛谷OJ P3803 【模板】多項式乘法（FFT） 題目思路：FFT模板題 AC程式碼： // luogu-judger-enable-o2 #include <stdio.h> #include <string.h> #include <iostream> #include < 2018.11.14 uoj#34. 多項式乘法（ntt） 傳送門 今天學習 n t t ntt 【Learning】多項式乘法與快速傅裏葉變換（FFT） alt 技術 cos 相同 es2017 define ostream 意思 呵呵 簡介： 　　FFT主要運用於快速卷積，其中一個例子就是如何將兩個多項式相乘，或者高精度乘高精度的操作。 　　顯然暴搞是$O(n^2)$的復雜度，然而FFT可以將其將為$O(n lg HDU 1402 A * B Problem Plus ——（大數乘法，FFT） 兩個 ret 處理 complex truct std spa strlen mes 　　因為剛學fft，想拿這題練練手，結果WA了個爽= =。 　　總結幾點犯的錯誤： 　　1.要註意處理前導零的問題。 　　2.一定要註意數組大小的問題。（前一個fft的題因為沒用到b數組， Python 普通最小二乘法（OLS）進行多項式擬合 zlabel predict ylabel model for font 結果 param col 多元函數擬合。如 電視機和收音機價格多銷售額的影響，此時自變量有兩個。 python 解法： import numpy as np import pandas as 51Nod 1028 - 大數乘法 V2（FFT） 【題目描述】 【思路】 FFT的基礎應用，把一個大數從低位到高位看成一個多項式，大數想乘看成多項式想乘，多項式的自變數 x x 2018.11.14 uoj#34. 多項式乘法（） 傳送門 N O I p Gym100783C Golf Bot（FFT） 超時 mat int -- open 二進制反轉 lan change ble https://vjudge.net/problem/Gym-100783C 題意： 給出n個數，然後有m次查詢，每次輸入一個數x，問x能否由n個數中2個及2個以下的數相加組成。 思 HDU 4609 3-idiots ——（FFT） ace 代碼 ++ per str [1] 兩個 isp 題目 　　這是我接觸的第一個關於FFT的題目，留個模板。 　　這題的題解見：http://www.cnblogs.com/kuangbin/archive/2013/07/24/3210565.html。 　　FFT 傅裏葉變換（FFT）的多相濾波結構實現 class hold es2017 要求 sca 接收機 .html mar try 作者：桂。 時間：2017-09-25 14:53:01 鏈接：http://www.cnblogs.com/xingshansi/p/7591868.html 前言 A*B problem（FFT） esp mat ble struct operator for fin void gist #include<iostream> #include<cstdio> #include<cstring> #include<cmath& 【learning】多項式乘法&fft type 表示 了解 這就是 () 學習 a記錄 b+ wap [吐槽] 　　以前一直覺得這個東西十分高端完全不會qwq 　　但是向lyy、yxq、yww、dtz等dalao們學習之後發現這個東西的代碼實現其實極其簡潔 　　於是趁著還沒有忘記趕緊來寫一篇博 　　（說 cuda編程-矩陣乘法（1） return mac cpu ims iostream oba 簡單的 oid memory 本方法采用簡單的單線程計算每組行和列乘加運算 代碼如下： #include <stdio.h> #include <stdlib.h> #include 藍橋杯-加法變乘法（java） tac chm init system area 需要 out nor clas 藍橋杯第六屆省賽題目-加法變乘法（java） 題目： 我們都知道：1+2+3+ ... + 49 = 1225 現在要求你把其中兩個不相鄰的加號變成乘號，使得結果為2015 比如： OI中的快速傅裏葉變換（FFT） ali 系列 我認 交流 cpp 實現 AS 需要 部分 快速傅裏葉變換（FFT） 前言 關於這篇文章 ? ? 非常高興能有機會來探討快速傅裏葉變換，也就是大家熟知的 \(FFT\) 在 \(OI\) 中的運用。以前了解過一次 \(FFT\) ，現在過了幾個月，數學和 \ $