機器學習 --- 軟間隔支援向量機

阿新 • • 發佈：2018-11-24

一、軟間隔支援向量機直觀理解

之前所介紹的支援向量機形式都是要求所有的樣本都要能被正確地劃分，這又被稱作"硬間隔支援向量機"，當資料是帶有噪聲的，就可能會產生一些脫離群體的點。在實際情況中，採用硬間隔的方式難以確定合適的核函式使得訓練樣本在特徵空間中線性可分，即使能確定某個核函式能進行很好的劃分，但模型可能也會存在過擬合的現象，導致模型的泛化能力較差。

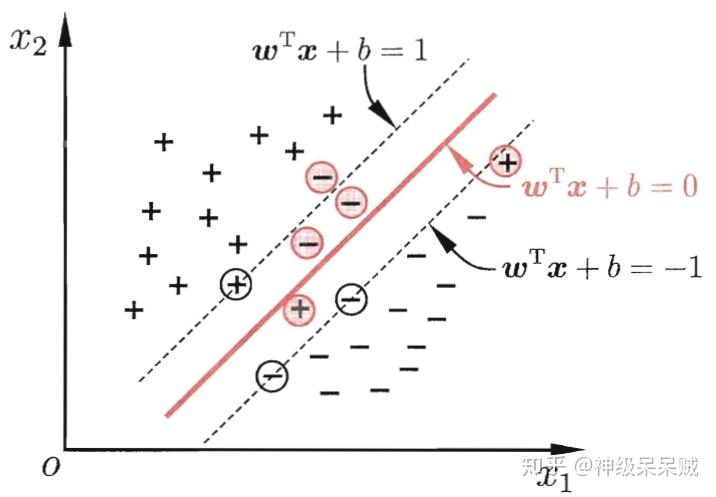
存在一些樣本點不滿足約束條件

軟間隔支援向量機旨在允許模型對一些離群點保持“容忍”態度。

二、軟間隔支援向量基本形式

在硬間隔模型中，約束條件：

$y_i(w^Tx_i+b)\geq 1 , \ \ \ \ \ i=1,2,...,m$

如果樣本存在噪聲，約束條件變成：

$y_i(w^Tx_i+b)\geq 1 -\xi_i , \ \ \ \ \ i=1,2,...,m$

這裡的 $\xi_i \geq 0$

表示第 $i$ 個樣本點允許偏離函式間隔的值，又稱作鬆弛變數。那麼新的優化方程為:

$min\ \frac{1}{2}\left| \left|w \right| \right|^2+C\sum_{i=1}^{m}{\xi_i} \ \ \ \ \ \ \qquad \qquad \qquad\qquad\qquad(1)$

$s.t \ \ y_i(w^Tx_i+b) \geq 1-\xi_i ,\ \ \ \ \ i=1,2,...,m$

$\ \ \ \ \ \ \ \xi_i\geq0 ,\ \ \ \ \ i=1,2,...,m$

這裡的 $C$ 是一個常量，又稱作懲罰係數。當 $C$ 值設定得很大時，目標函式後一項所佔權重比也會很大，優化過程中將會著重優化後一項，即減小第 $i$ 個樣本點允許偏離函式間隔的值，模型退化成硬間隔型式，則可能會出現過擬合。同樣地，當 $C$ 值設定的非常小時，可能出現欠擬合情況。

之前提到的鬆弛變數 $\xi_i$ ：

$\xi_i=l_{0/1}(y_i(w^Tx_i+b)-1)$

其中 $l_{0/1}$ ：

$l_{0/1}=\left\{ \begin{aligned} & 1, \ z<0 \\ & 0, \ otherwise \\ \end{aligned} \right.$

由於 $l_{0/1}$

非凸，非連續，在求解目標函式時較為困難。因此還有一些其他的替代損失函式：

hinge損失： $l_{hinge}(z)=max(0,1-z)$

指數損失： $l_{exp}(z)=exp(-z)$

對率損失： $l_{log}(z)=log(1+exp(-z))$

三、模型求解

由拉格朗日乘子法，將(1)式轉化成：

$L(w,b,\xi,\alpha,\mu)=\frac{1}{2}\left| \left| w \right| \right|^2+C\sum_{i=1}^{m}{\xi_i}+\sum_{i=1}^{m}{\alpha_i(1-\xi_i-y_i(w^Tx_i+b))-\sum_{i=1}^{m}{\mu_i\xi_i}} \ \ \ \ \ (2)$