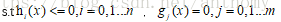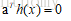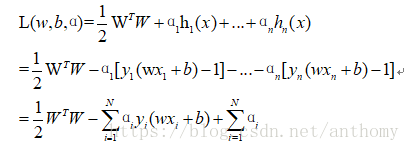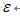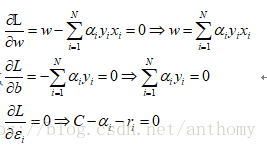一、 引言

最近在機器學習課上，學到的《機器學習實戰》第六章的支援向量機，這部分內容非常多，不僅要會程式設計和測試，還要理解它的數學基礎，這裡對這部分的學習進行一些總結。

二、 SVM的數學原理

從一個簡單的二分問題開始說吧：

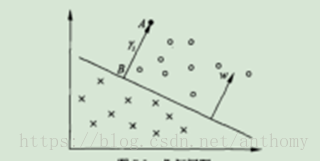
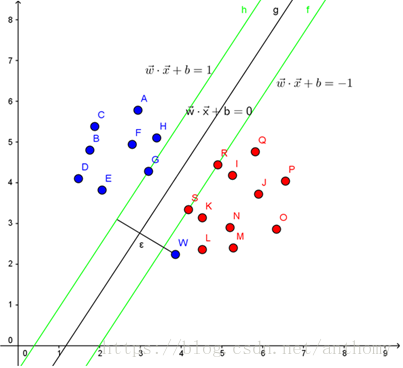
我們要把這兩類不同的點區分開，那麼在這個二維平面上就是找條直線，儘量使得這些點更好的分隔開，那麼這條直線可以表示為AX+BY+C=0.

在資料集中自然是多種屬性的，這時候就可以看成是n維空間，這個時候要區分這些資料，我們的目標是需要找到一個n-1維的超平面，這個超平面可以將資料分成兩類，, 可以表示為W1X1+W2X2+…+WnXn+b=0（等價於 ）每部分資料屬於一個類別，這樣的超平面其實有很多，我們需要找到一個最好的，我們希望這個超平面到每邊最近資料點的距離是最大的，稱為最大間隔超平面，如何找到最好的分割面呢？就是找W的係數，即權值。

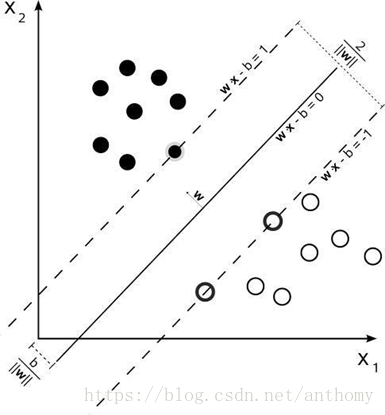
還是以二維平面為例，假設距離區分直線的兩條直線分別為d1和d2,支援向量機找最優權值的策略即使，先到最邊上的點，再找到這兩個距離之和D=d1+d2,然後求解D的最大值.

分介面是二維的，那麼分介面可以表示為W1X1+W2X2+b=0,上分界線可以表示成W1X1+W2X2+b=1，下分界線可以表示成W1X1+W2X2+b=0-1；那麼D就等於兩直線的距離,由初等數學中兩直線距離公式可知，,這裡的W=(w1,w2),是一個向量，|W|為向量的距離，那麼 ,下分界線同理，所以,要使得D最大（期望訓練資料中的每個點到超平面的距離最大），即。

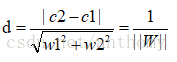
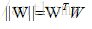
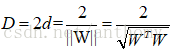
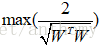
為了方便後續的計算，我們可以引入其對偶問題，這樣優化問題變成了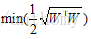，約束條件為 

分介面以上的點有 ，我們可以假設它的標籤y為1，所以分介面以下的點有，我們可以假設它的標籤y為-1。 這樣的話對於上下兩條分界線外的點，約束條件乘以他們的標籤，我們可以修改約束條件為 ，也等價於，又因為求解，不如求解等效的 ，

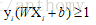
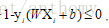
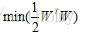
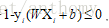
所以最終的優化問題變成了 和約束條件，這麼轉換的原因是為了在形式上滿足KKT條件和拉格朗日乘子法，方便我們接下來求解優化問題中的W和b.

而上下邊界上的點就是支援向量，這些點很關鍵，這也是”支援向量機“命名的由來。

概括來說SVM的核心思想就是找到不同類別之間的分介面，使得兩類樣本儘量落在面的兩邊，而且離分介面儘量遠。

這裡再介紹一下KKT條件和拉格朗日乘子法。

通常情況下我們要求解的最優化問題可以分為三類情況：

<1>無約束的優化問題

Min(f(x))或Max(f(x))

<2>有等式約束的優化問題

Min(f(x))或Max(f(x)) 

<3>有不等式約束的優化問題

Min(f(x))或Max(f(x)) 

對於第一類問題的求解，在高數上我們已經學習過，就是先求f(x)的導數，然後令其為零，可以求得候選最優值，再在這些值中進行驗證，如果是凸函式，就可以保證最優解。

對於第二類問題，一般使用的是拉格朗日乘子法，就是把目標函式和約束條件乘以一個係數寫成一個式子，這個式子稱為拉格朗日函式，係數稱為拉格朗日乘子。即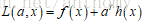 a是橫向量，h(x)是列向量。

再通過拉格朗日函式對各個變數Xi 求偏導，令其為零，求得候選值得集合，再通過驗證得到最優值。

對於第三類優化問題，一般使用的方法KKT條件，同樣地，我們把所有的等式、不等式約束與f(x)寫為一個式子，也叫拉格朗日函式，係數也稱拉格朗日乘子，即

通過一些條件，可以求出最優值的必要條件，這個條件稱為KKT條件。

這些條件表示為：

<1>L(a,b,x)對x求導為零;

<2>g(x)=0;

<3> 

因為約束條件h(x)<=0,如果要滿足這個等式，必須有a=0或者h(x)=0，這個是SVM很多性質的來源，如支援向量的概念。

再回到我們上面提到的SVM分類器，從我們分析的結果 ，。滿足使用拉格朗日乘子法的條件。

1.    求一個最優化問題

2.    存在不等式約束

3.    目標函式是凸函式

這個也是滿足的。

所以引入拉格朗日乘子法，優化的目標改變為：

接下來求偏導，令其等於零：

這時候再帶回L中，把w和b消掉

求解最開始的函式的最小值等價到現在就是求解W的最大值。現在的問題變成了：

其中是KKT條件中的要求。

我們可以發現點w是一個異常點，，這在資料中是非常常見的，屬性上與其附近的點很相近，但標籤卻截然不同，為了解決這個這個問題，我們引入了鬆弛變數

修改之後的約束條件為 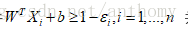並且 

運用拉格朗日乘子法之後的公式就變成了：

我們在優化的時候，儘可能使得鬆弛變數之和最小，常數C是決定鬆弛變數之和對優化問題的影響程度，越大表明影響越嚴重，C是一個大於零的值。

現在把所有問題綜合起來：

，看起來相當複雜是吧，不用擔心，但是該怎麼求還是求。

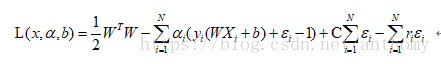
然後對 w,b,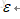分別求導數

因為 ，所以，即，又因為之前就得到 ，所以

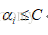
將上述條件代入目標函式中消掉w,b,r,最終得到：

發現 也一起消掉了，並且目標函式也變成了沒加鬆弛變數之前的一樣，但是相比之前添加了新的條件

最終的優化問題就變成了

接下來就是要去找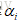最優解了。

這裡就用的到SMO演算法了。

1996年，John Platt釋出了一個稱為SMO的強大演算法，用於訓練SVM。SMO表示序列最小優化（Sequential Minimal Optimization）。SMO是將大優化問題分解為多個小優化問題來求解，小優化問題一般很容易求解，並且對他們進行順序求解的結果與將他們作為整體來求得結果是完全一樣的，而且這樣求解的時間會短很多。

SMO方法：

概要：SMO方法的中心思想是每次取一對αi和αj，調整這兩個值。增大其中一個，同時減小另外一個， αi和αj是具有一定函式關係的，所以說只有一個引數而已，得到了這些 ，就很容易計算出權重向量w了，並得到相應的超平面。

演算法過程:

1.初始化α為0；

2.在每次迭代中(小於等於最大迭代數），找到第一個不滿足KKT條件的訓練資料，對應的αi，在其它不滿足KKT條件的訓練資料中，找到誤差最大的x，對應的index的αj，αi和αj組成了一對，根據約束條件調αi, αj。

不滿足KKT條件的公式

演算法過程的數學表達：

最後來提一下核函式的概念。

再回到我們上面提到構造，都是基於資料完全線性可分，支援向量機（SVM）是一個二分類器，是一個線性的分類器

我們在之前所述是線上性問題的基礎上構造的，那如果是非線性問題呢，比如說之前提到的分界線，如果變成是一個曲線呢，怎麼得到這個曲線方程呢，在多維空間中就很更麻煩。但是數學家們提供瞭解決方法，非線性問題對映到高緯度後，會變成一個線性問題了。

比如：二維下的一個點<x1,x2><x1,x2>, 可以對映到一個5維空間，這個空間的5個維度分別是:x1,x2,x1x2,x12,x22x1,x2,x1x2,x12,x22。

對映到高維度，有兩個問題：一個是如何對映？另外一個問題是計算變得更復雜了。

我們可以使用核函式(Kernel function)來解決這個問題

從上述演算法過程的數學表達我們不難看出，關於向量X的計算，總是在計算兩個向量的內積K(x1,x2)= <x1,x2>，所以在高緯空間裡，公式的變化只有計算低維空間下的內積<x1,x2>變成了計算高緯空間下的內積<x1’,x2’>,核函式提供的方法就是通過原始空間的向量值計算高緯空間的內積，而不去管這個對映的方式。

核函式有很多種，一般使用的是高斯核（徑向基函式（radial basisfunction））

可以通過調節σ來匹配維度的大小，σ越大，維度越低。

三、 程式除錯

1.開啟testSet.txt檔案，得到每行的類標籤和整個資料矩陣，類標籤中的-1改用0代替，為了方便後續的處理

2.簡化版的SMO

虛擬碼大致如下：（不同層次的迴圈用顏色匹配）

建立一個alpha向量並將其初始化為0向量，當迭代次數小於最大迭代次數(外迴圈)，對資料集中每個資料向量(內迴圈)，

如果該資料向量可以被優化：隨機選擇另外一個數據向量，同時優化這個向量

如果兩個向量都不能被優化，退出內迴圈

如果所有向量都未被優化，增加迭代數，進入下次迴圈。

2.1 、檢查alpha[j]是否改變，退出for迴圈，alpha[i]和alpha[j]進行同樣大小的改變，一個增加，一個減小，進行優化之後設定常數項b.

2.2、觀察alpha矩陣，去除掉其中的零元素

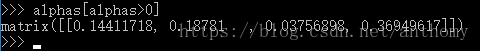
2.3、檢視那些資料點是支援向量，非零的alpha值是支援向量

簡化版SMO對於小規模資料集可用，但對於大規模資料，執行速度會變慢。

完整的SMO演算法通過一個外迴圈來選擇alpha值，選擇過程在兩種方式之間交替：

1-在所有資料集上進行單遍掃描； 2-在非邊界（不等於邊界0/C的值）alpha中實現單遍掃描。實現非邊界值的掃描時，需要建立alpha列表，然後對錶進行遍歷，跳過那些已知不會改變的alpha值。

選擇第一個alpha後，通過內迴圈來選擇第二個alpha，優化過程中選擇最大步長的方式獲取第二個alpha。

完整的Platt SMO演算法包括以下三個部分，對應的程式大家可以到《機器學習實戰》第六章找到。

<1>用於清理程式碼的資料結構和3個用對E快取的輔助函式。

<2>優化過程：（選擇第二個alpha）與之前簡化版SMO差別不大，不過添加了自己的資料結構，在oS中傳遞，使用selectJ代替selectJrand來選擇則第二個alpha，alpha改變時更新Ecache值

<3>外迴圈（包含了kernel函式-高斯核)

經過迭代得到權值W。

3.對資料進行分類的驗證（對第一個資料點分類，得到的值如果大於零，則屬於1類，如果小於零則屬於-1類，並通過命令得到其原始的標籤驗證分類結果的正確性）再對第二個、第三個資料點進行驗證。

4.觀察k1=1.3測試錯誤率，訓練錯誤率，支援向量個數。

5.手寫識別問題

流程 
（1）收集資料：提供原始資料的文字檔案 
（2）準備資料：基於手寫二值影象構造向量 
（3）分析資料：對影象向量進行目測 
（4）訓練演算法：採用兩種不同的核函式，並對徑向基核函式採用不同設定來執行SMO演算法 

（5）測試演算法：編寫測試函式來測試不同核函式並計算error rate 

匯入資料進行測試：kTup=('rbf', 10)

有50個支援向量，測試資料錯誤率為1.6%

四、總結

演算法的實現來源於數學，數學是一個非常強大的工具，深刻了解到數學上的邏輯性，會幫助我們理解程式每一個步驟，在程式設計時更加的有效率。

這次只是實現了一些對簡單問題的分類，接下來有時間的話，想去尋找一些有意思的一些資料集，希望在上面運用支援向量機的方法，再對比一些其他的分類方法，看看支援向量機的優勢與不足。

非常感謝閱讀！如有不足之處，請留下您的評價和問題。

參考文獻

【1】    深入理解拉格朗日乘子法（LagrangeMultiplier) 和KKT條件

【2】    解密SVM系列（三）：SMO演算法原理與實戰求解

【3】  機器學習實戰 - 讀書筆記(06) – SVM支援向量機

https://www.cnblogs.com/steven-yang/p/5658362.html

【4】 《機器學習實戰》-PeterHarrington

【5】 《統計學習方法》-李航