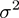Stanford機器學習筆記-8. 支援向量機(SVMs)概述
8. Support Vector Machines(SVMs)
Content
8. Support Vector Machines(SVMs)
8.1 Optimization Objection
8.2 Large margin intuition
8.3 Mathematics Behind Large Margin Classification
8.4 Kernels
8.5 Using a SVM
8.5.1 Multi-class Classification
8.5.2 Logistic Regression vs. SVMs
8.1 Optimization Objection
支援向量機(Support Vector Machine: SVM)是一種非常有用的監督式機器學習演算法。首先回顧一下Logistic迴歸,根據log()函式以及Sigmoid函式的性質,有:
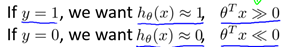
同時,Logistic迴歸的代價函式(未正則化)如下:
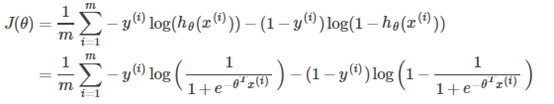
為得到SVM的代價函式,我們作如下修改:

因此,對比Logistic的優化目標

SVM的優化目標如下:
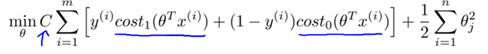
注1:事實上,上述公式中的Cost0與Cost1函式是一種稱為hinge損失的替代損失(surrogate loss)函式,其他常見的替代損失函式有指數損失
注2:注意引數C和λ的對應關係: C與(1 / λ)成正相關。
8.2 Large margin intuition
根據8.1中的代價函式,為使代價函式最小,有如下結論:
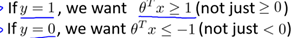
現假設C很大(如C=100000),為使代價函式最小,我們希望
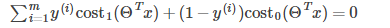
所以代價函式就變為:
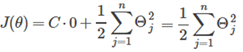
所以問題就變成:

該問題最後的優化結果是找到具有"最大間隔"(maximum margin)的劃分超平面,所以支援向量機又稱大間距分類器(large margin classifier)。那麼什麼是間隔? 為什麼這樣優化就可以找到最大間隔?首先,我們通過圖8-1所示的二維的0/1線性分類情況來直觀感受。
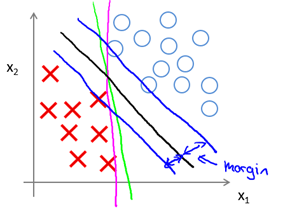
圖8-1 SVM Decision Boundary: Linearly separable case
直觀上,應該去找位於兩類訓練樣本"正中間"的劃分超平面,即圖8-1的黑色直線(二維),因為該劃分超平面對訓練樣本區域性擾動的"容忍"性最好。例如,圖中的粉色和綠色直線,一旦輸入資料稍有變化,將會得到錯誤的預測。換言之,這個劃分超平面所產生的分類結果是最魯棒的,對要預測資料集的泛化能力最強。而兩條藍色直線之間的距離就稱為間隔(margin)。下一節將從數學角度來解釋間隔與最大間隔的優化原理。
8.3 Mathematics Behind Large Margin Classification
首先介紹一些數學知識。
- 2-範數(2-norm): 也可稱長度(length),是二維或三維空間向量長度的推廣,向量u記為||u||。例如,對於向量u = [ u1, u2, u3, u4],||u|| = sqrt(u1^2 + u2^2 + u3^2 + u4^2)
- 向量內積(Vector Inner Product): 設向量a = [a1, a2, … , an],向量b = [b1, b2, … , bn],a和b的的內積定義為:a · b = a1b1 + a2b2 + … + anbn 。向量內積是幾何向量數量積(點積)的推廣,可以理解為向量a在向量b上的投影長度(範數)和向量b的長度的乘積。
所以有:

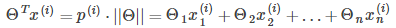
其中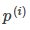 是
是 在
在 向量上的投影長度。
向量上的投影長度。
所以,8.2節得到的優化問題可以轉為如下形式:
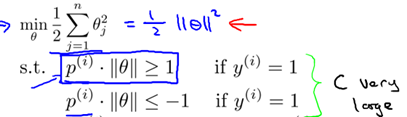
分界線為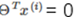 ,所以可知
,所以可知 和分界線正交(垂直),並且當
和分界線正交(垂直),並且當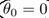 時,分界線過原點(歐式空間)。為使目標最優(取最小值)且滿足約束,
時,分界線過原點(歐式空間)。為使目標最優(取最小值)且滿足約束,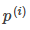 應該儘可能大,這樣就要求間距儘可能的大。直觀的如圖8-2所示,圖左為間距較小的情況,此時的
應該儘可能大,這樣就要求間距儘可能的大。直觀的如圖8-2所示,圖左為間距較小的情況,此時的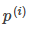 較小,為滿足約束,導致目標函式變大,圖右為最大間距的情況,此時的
較小,為滿足約束,導致目標函式變大,圖右為最大間距的情況,此時的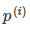 是最大的,所以目標可以儘可能的小。
是最大的,所以目標可以儘可能的小。

圖8-2 兩種不同間距的情況
8.4 Kernels
上述的討論都是基於線性可分的樣本,即存在一個劃分超平面可以將訓練樣本正確分類,然而現實世界存在大量複雜的,非線性分類問題(如4.4.2節的異或/同或問題)。Logistic迴歸處理非線性問題可以通過引入多項式特徵量作為新的特徵量;神經網路通過引入隱藏層,逐層進化解決非線性分類問題;而SVM是通過引入核函式(kernel function)來解決非線性問題。具體做法如下:
-
對於給定輸出x, 規定一定數量的landmarks,記為
 ;
;
-
將x,
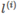 作為核函式的輸入,得到新的特徵量
作為核函式的輸入,得到新的特徵量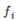 ,若將核函式記為similarity(),則有
,若將核函式記為similarity(),則有
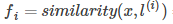 ,其中
,其中 與
與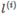 為一一對應;
為一一對應; -
將新的特徵量替代原有特徵量,得到假設函式如下:

現在有兩個問題,
- 如何選擇landmarks?
- 用什麼樣的核函式 ?
對於第一個問題,可以按照如下方式,即將訓練集的輸入作為landmarks

所以特徵量的個數與訓練集的個數相等,即n = m,所以帶有核的SVM變為如下形式:

對於第二個問題,常用的核函式有線性核,高斯核,多項式核,Sigmoid核,拉普拉斯核等,現以常用的高斯核(Gaussian)為例。

高斯核具有如下性質:

也就是說,如果x和landmark接近,那麼核函式的值也就是新的特徵量將會接近1,而如果x和landmark距離很遠,那麼核函式的值將會接近0.
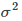 是高斯核的引數,它的大小會影響核函式值的變化快慢,具體的,圖8-3是一個二維情況下的特殊例子,但是所含有的性質是可推廣的。即
是高斯核的引數,它的大小會影響核函式值的變化快慢,具體的,圖8-3是一個二維情況下的特殊例子,但是所含有的性質是可推廣的。即 越大,核函式變化(下降)越緩慢,反之,
越大,核函式變化(下降)越緩慢,反之,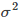 越小,核函式變化越快。
越小,核函式變化越快。

圖8-3 引數對高斯核的影響舉例
- 如何選擇引數?
下面對SVM的引數對偏差和方差的影響做簡要分析:
- C: 由於C和(1 / λ)正相關,結合6.4.2節對λ的分析有:
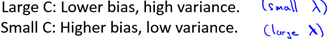

8.5 Using a SVM
上文簡單的介紹了SVM的優化原理以及核函式的使用方式。在實際應用SVM中,我們不需要自己去實現SVM的訓練演算法來得到引數 ,通常是使用現有的軟體包(如liblinear, libsvm)。
,通常是使用現有的軟體包(如liblinear, libsvm)。
但是下面的工作是我們需要做的:
- 選擇引數C的值
-
選擇並實現核函式
-
如果核函式帶引數,需要選擇核函式的引數,例如高斯核需要選擇
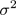
- 如果無核(選擇線性核),即給出線性分類器,適用於n大,m小的情況
- 選擇非線性核(如高斯核),適用於n小,m大的情況
-
如果核函式帶引數,需要選擇核函式的引數,例如高斯核需要選擇
下面是需要注意的地方:
- 在使用核函式之前要對特徵量進行規範化
- 並不是所有的函式是有效的核函式,它們必須滿足Mercer定理。
- 如果想要通過訓練得到引數C或者核函式的引數,應該是在訓練集和交叉檢驗集上進行,,參見6.3節。
8.5.1 Multi-class Classification

8.5.2 Logistic Regression vs. SVMs