一、什麼是MerkleTree

  MerkleTree，是一種樹（資料結構中所說的樹），網上大都稱為MerkleHashTree,這是因為它所構造的MerkleTree的所有節點都是Hash值。MerkleTree具有以下特點：

1.它是一種樹，可以是二叉樹，也可以多叉樹，無論是幾叉樹，它都具有樹結構的所有特點；

2.Merkle樹的葉子節點上的value，是由你指定的，這主要看你的設計了，如MerkleHashTree會將資料的Hash值作為葉子節點的值；

3非葉子節點的value是根據它下面所有的葉子節點值，然後按照一定的演算法計算而得出的。

  在特幣網路中， Merkle樹被用來歸納一個區塊中的所有交易， 同時生成整個交易集合的數字指紋， 且提供了一種校驗區塊是否存在某交易的有效效途徑。 生成一棵完整的Merkle樹需要遞迴地對雜湊節點對進行雜湊， 並將新生成的雜湊節點插入到Merkle樹中， 直到只剩一個雜湊節點， 該節點就是Merkle樹的根。 在比特幣的Merkle樹中兩次使用到了SHA256演算法， 因此其加密雜湊演算法也被稱為double-SHA256。

  當N個數據元素經過加密後插入Merkle樹時，你至多計算2*log2(N)次就能檢查出任意某資料元素是否在該樹中， 這使得該資料結構非常有效。

Merkle樹是自底向上構建的。 在如下的例子中， 我們從A、 B、 C、 D四個構成Merkle樹樹葉的交易開始，如下圖。起始時所有的交易都還未儲存在Merkle樹中，而是先將資料雜湊化， 然後將雜湊值儲存至相應的葉子節點。 這些葉子節點分別是HA、 HB、 HC和HD：

                                                                                                 H~A~ = SHA256(SHA256(交易A))

  通過串聯相鄰葉子節點的雜湊值然後雜湊之， 這對葉子節點隨後被歸納為父節點。 例如， 為了建立父節點HAB， 子節點A和子節點B的兩個32位元組的雜湊值將被串聯成64位元組的字串。 隨後將字串進行兩次雜湊來產生父節點的雜湊值:

                                                                                                   H~AB~=SHA256(SHA256(H~A~ + H~B~))

  繼續類似的操作直到只剩下頂部的一個節點， 即Merkle根。 產生的32位元組雜湊值儲存在區塊頭， 同時歸納了四個交易的所有資料。

二、 Merkle Tree的應用

2.1對比與驗證

  目前， 在計算機領域，Merkle Tree大多用來進行比對以及驗證處理。比在處理比對或驗證的應用場景中時，特別是在分散式環境下進行比對或驗證時，Merkle Tree會大大減少資料的傳輸量以及計算的複雜度。例如，假如是 15,16.......30是一個個資料塊的hash值，我把這些資料從A傳輸到B，資料傳輸到B後，我想驗證下傳輸到B上的資料的有效性型（驗證資料是否在傳輸過程中發生變化），只需要驗證A 和 B上所構造的Merkle。

   Tree的root節點值是否一致即可，如果一致，表示資料是有效的，傳輸過程中沒有發生改變。假如在傳輸過程中，15對應的資料被人篡改，通過Merkle Tree很容易定位找到（因為此時，節點0,1,3,7,15對應的hash值都發生了變化），定位的時間複雜度為O（log(n））。

2.2認證

為了證明區塊中存在某個特定的交易，一個節點只需要計算log2(N)個32位元組的雜湊值， 形成一條從特定交易到樹根的認證路徑或者Merkle路徑即可。 隨著交易數量的急劇增加， 這樣的計算量就顯得異常重要， 因為相對於交易數量的增加， 以基底為2的交易數量的對數的增長會緩慢許多。 這使得比特幣節點能夠高效地產生一條10或者12個雜湊值（ 320-384位元組） 的路徑， 來證明了在一個巨量位元組大小的區塊中上千交易中的某筆交易的存在。

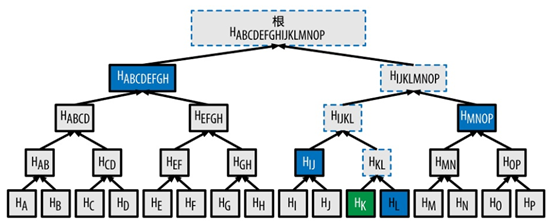
在下圖中，一個節點能夠通過生成一條僅有4個32位元組雜湊值長度（ 總128位元組） 的Merkle路徑， 來證明區塊中存在一筆交易K。該路徑有4個雜湊值（在圖7-5中由藍色標註） HL、 HIJ、 HMNOP和HABCDEFGH。 由這4個雜湊值產生的認證路徑，再通過計算另外四對雜湊值HKL、 HIJKL、 HIJKLMNOP和Merkle樹根（ 在圖中由虛線標註） ， 任何節點都能證明HK（ 在圖中由綠色標註） 包含在Merkle根中。

如何認證：

1.準備階段：得到Merkle認證路徑，即藍色標註；

2.計算階段：

a.由HK（待驗證的節點）和認證路徑中的HL計算可以得到HKL；

b.由HKL和認證路徑中的HIJ可以得到HIJKL；

以此類推可以得到根，只要比較根的大小，就可以知道HK是否在這個區塊中了。