關於資料結構中樹結構的相關分享

一、傳統的資料結構中的樹結構

• 樹結構是一種非線性儲存結構，儲存的是具有“一對多”關係的資料元素的集合。

• 其中，討論較多的是二叉樹。二叉樹的每個結點至多隻有二棵子樹(不存在度大於2的結點)，二叉樹的子樹有左右之分，次序不能顛倒。

1.1 二叉查詢樹

• 二叉查詢樹定義：又稱二叉排序樹或二叉搜尋樹。二叉排序樹或者是一棵空樹，具有下列性質：

1. 左子樹上所有結點的值均小於它的根結點的值；右子樹均大於或等於它的根結點的值；
2. 左、右子樹也分別為二叉排序樹；

• 特點：
  • 二叉查詢樹的性質：對二叉查詢樹進行中序遍歷，即可得到有序的數列。
  • 二叉查詢樹的高度決定了二叉查詢樹的查詢效率。

1.2 平衡二叉樹

• 為了讓二叉搜尋樹的期望高度為 log2n，即使得各操作的時間複雜度為 O(log2n), 於是有了平衡二叉樹(即 AVL樹)。
• 定義：它是一棵空樹或它的左右兩個子樹的高度差的絕對值不超過1，並且左右兩個子樹都是一棵平衡二叉樹。
• 最小二叉平衡樹的節點的公式如下： F(n)=F(n-1)+F(n-2)+1

1.3 平衡二叉樹之紅黑樹

• 定義：紅黑樹是一種自平衡二叉查詢樹，其典型的用途是實現關聯陣列(比如 C++ 中的 STL 中的map,和 set 等關聯式容器都是基於紅黑樹的)。

• 它可以在O(logn)時間內做查詢，插入和刪除，這裡的n是樹中元素的數目。這使得它可以適用於實時應用（real time application）。

• 紅黑樹還是2-3-4樹的一種等同，它們的思想是一樣的，只不過紅黑樹是2-3-4樹用二叉樹的形式表示的。

• 2-3-4 樹把資料儲存在叫做元素的單獨單元中。它們組合成節點。每個節點都是下列之一：

  • 2-節點，就是說，它包含 1 個元素和 2 個兒子；
  • 3-節點，就是說，它包含 2 個元素和 3 個兒子；
  • 4-節點，就是說，它包含 3 個元素和 4 個兒子。

• 如下圖(所示)：

• 紅黑樹的性質：
  紅黑樹是每個節點都帶有顏色屬性的二叉查詢樹，顏色為紅色或黑色。除了二叉查詢樹特有性質之外，紅黑樹還增加了如下要求:

性質1. 節點是紅色或黑色，根是黑色，所有葉子都是黑色

性質2. 每個紅色節點必須有兩個黑色的子節點。(從每個葉子到根的所有路徑上不能有兩個連續的紅色節點，即紅黑相間)，從任一節點到其每個葉子的所有簡單路徑都包含相同數目的黑色節點(簡稱黑高)。

• 紅黑樹的圖例，如下：

• 性質分析：
  • 有了上面的幾個性質作為限制，即可避免二叉查詢樹退化成單鏈表的情況。但是，僅僅避免這種情況還不夠，這裡還要考慮某個節點到其每個葉子節點路徑長度的問題。如果某些路徑長度過長，那麼，在對這些路徑上的及誒單進行增刪查操作時，效率也會大大降低。這個時候性質4和性質5用途就凸顯了，有了這兩個性質作為約束，即可保證任意節點到其每個葉子節點路徑最長不會超過最短路徑的2倍。
  • 原因如下：
  • 當某條路徑最短時，這條路徑必然都是由黑色節點構成。當某條路徑長度最長時，這條路徑必然是由紅色和黑色節點相間構成（性質限定了不能出現兩個連續的紅色節點）。而性質又限定了從任一節點到其每個葉子節點的所有路徑必須包含相同數量的黑色節點。此時，在路徑最長的情況下，路徑上紅色節點數量 = 黑色節點數量。該路徑長度為兩倍黑色節點數量，也就是最短路徑長度的2倍。(如下圖)

• 紅黑樹的自平衡調整操作：
  • 因為每一個紅黑樹也是一個特化的二叉查詢樹，因此紅黑樹上的只讀操作與普通二叉查詢樹上的只讀操作相同。
  • 此外，在紅黑樹上進行插入操作和刪除操作會導致不再符合紅黑樹的性質。恢復紅黑樹的性質需要少量(O(logn))的顏色變更(實際是非常快速的)和不超過三次樹旋轉結構變更(對於插入操作是兩次)。
  • 雖然插入和刪除很複雜，但操作時間仍可以保持為 O(logn) 次。
  • 具體的插入、構建、刪除、和調整操作(程式碼相關的)，可參見維基百科。
  • 紅黑樹調整

1.4 B 樹

• B樹也是一種用於查詢的平衡樹，但是它不是二叉樹，它是多路搜尋樹。
• 定義： B樹（B-tree）是一種樹狀資料結構，能夠用來儲存排序後的資料。這種資料結構能夠讓查詢資料、循序存取、插入資料及刪除的動作，都在對數時間內完成。B樹即一般化的二叉查詢樹，可以擁有多於2個子節點。與自平衡二叉查詢樹不同，B樹為系統最優化大塊資料的讀和寫操作。B-tree演算法減少定位記錄時所經歷的中間過程，從而加快存取速度。這種資料結構常被應用在資料庫和檔案系統的實現上。
  
  
• B樹作為一種多路搜尋樹（並不是二叉的）的性質：
  1. 定義任意非葉子結點最多隻有M個兒子；且M>2；
  2. 根結點的兒子數為[2, M], 非根非葉子結點的兒子數為[M/2, M]；
  3. 每個結點存放至少 M/2-1（取上整）和至多M-1個關鍵字；（至少2個關鍵字）
  4. 非葉子結點的關鍵字個數 = 指向兒子的指標個數-1；
  5. 非葉子結點的關鍵字有序：K[1], K[2], …, K[M-1]；且K[i] < K[i+1]；
  6. 非葉子結點的指標：P[1], P[2], …, P[M]；其中P[1]指向關鍵字小於K[1]的子樹，
     P[M]指向關鍵字大於K[M-1]的子樹，其它P[i]指向關鍵字屬於(K[i-1], K[i])的子樹；
  7. 所有葉子結點位於同一層；
     
     
• M=3 的 B 樹示例圖：
  
  
  
• 比起正常的平衡二叉樹，B樹每個節點顯然能儲存的資料更多，在查詢資料方面也顯得比較高效。
• B樹建立的示意圖：
  
  
  

1.5 B+樹

B+樹是B樹的變體，也是一種多路搜尋樹：

1. 其定義基本與B-樹相同，除了：
2. 非葉子結點的子樹指標與關鍵字個數相同；
3. 非葉子結點的子樹指標P[i]，指向關鍵字值屬於[K[i], K[i+1])的子樹（B-樹是開區間）；
4. 為所有葉子結點增加一個鏈指標；
5. 所有關鍵字都在葉子結點出現；

• 下圖為 M=3 的 B+ 樹的示意圖

• B+樹的搜尋與B樹也基本相同，區別是B+樹只有達到葉子結點才命中（B樹可以在非葉子結點命中），其效能也等價於在關鍵字全集做一次二分查詢；

B+ 樹的性質：
1.所有關鍵字都出現在葉子結點的連結串列中（稠密索引），且連結串列中的關鍵字恰好是有序的；
2.不可能在非葉子結點命中；
3.非葉子結點相當於是葉子結點的索引（稀疏索引），葉子結點相當於是儲存（關鍵字）資料的資料層；
4.更適合檔案索引系統。

• B + 樹的建立示意圖：
  
  
  

• B 樹和 B+ 樹的異同：

  • 結構上
    • B樹中關鍵字集合分佈在整棵樹中，葉節點中不包含任何關鍵字資訊，而B+樹關鍵字集合分佈在葉子結點中，非葉節點只是葉子結點中關鍵字的索引；
    • B樹中任何一個關鍵字只出現在一個結點中，而B+樹中的關鍵字必須出現在葉節點中，也可能在非葉結點中重複出現；
  • 效能上（也即為什麼說B+樹比B樹更適合實際應用中作業系統的檔案索引和資料庫索引？）
    • 不同於B樹只適合隨機檢索，B+樹同時支援隨機檢索和順序檢索；
    • B+樹的磁碟讀寫代價更低。B+樹的內部結點並沒有指向關鍵字具體資訊的指標，其內部結點比B樹小，盤塊能容納的結點中關鍵字數量更多，可一次性將索引讀入記憶體中可以查詢的關鍵字也就越多，相對的，IO讀寫次數也就降低了。而IO讀寫次數是影響索引檢索效率的最大因素。也就是說同樣資料情況下，B+ 樹會 B 樹更加“矮胖”，因此查詢效率更快。
    • B+樹的查詢效率更加穩定。B樹搜尋有可能會在非葉子結點結束，越靠近根節點的記錄查詢時間越短，只要找到關鍵字即可確定記錄的存在，其效能等價於在關鍵字全集內做一次二分查詢。而在B+樹中，順序檢索比較明顯，隨機檢索時，任何關鍵字的查詢都必須走一條從根節點到葉節點的路，所有關鍵字的查詢路徑長度相同，導致每一個關鍵字的查詢效率相當。
    • （資料庫索引採用B+樹的主要原因是，）B-樹在提高了磁碟IO效能的同時並沒有解決元素遍歷的效率低下的問題。B+樹的葉子節點使用指標順序連線在一起，只要遍歷葉子節點就可以實現整棵樹的遍歷。而且在資料庫中基於範圍的查詢是非常頻繁的，而B樹不支援這樣的操作（或者說效率太低）。

1.6 B* 樹

• B* 樹是 B+ 樹的變體，在B+樹的非根和非葉子結點再增加指向兄弟的指標，將結點的最低利用率從1/2提高到2/3。
  
  

• 圖示如下：
  

• B* 樹定義了非葉子結點關鍵字個數至少為(2/3)*M，即塊的最低使用率為2/3（代替B+樹的1/2）；

• B+樹的分裂：當一個結點滿時，分配一個新的結點，並將原結點中1/2的資料複製到新結點，最後在父結點中增加新結點的指標；B+樹的分裂隻影響原結點和父結點，而不會影響兄弟結點，所以它不需要指向兄弟的指標；

• B*樹的分裂：當一個結點滿時，如果它的下一個兄弟結點未滿，那麼將一部分資料移到兄弟結點中，再在原結點插入關鍵字，最後修改父結點中兄弟結點的關鍵字（因為兄弟結點的關鍵字範圍改變了）；如果兄弟也滿了，則在原結點與兄弟結點之間增加新結點，並各複製1/3的資料到新結點，最後在父結點增加新結點的指標；

所以，B*樹分配新結點的概率比B+樹要低，空間使用率更高。

二、字典樹 ( Trie樹 )

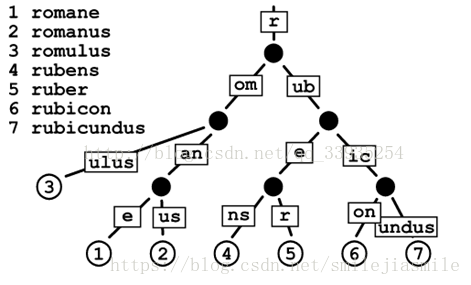
Tire樹稱為字典樹，又稱單詞查詢樹，Trie樹，是一種樹形結構，是一種雜湊樹的變種。典型應用是用於統計，排序和儲存大量的字串（但不僅限於字串），所以經常被搜尋引擎系統用於文字詞頻統計。它的優點是：利用字串的公共字首來減少查詢時間，最大限度地減少無謂的字串比較，查詢效率比雜湊樹高。

Tire樹的三個基本性質：

1. 根節點不包含字元，除根節點外每一個節點都只包含一個字元；
2. 從根節點到某一節點，路徑上經過的字元連線起來，為該節點對應的字串；
3. 每個節點的所有子節點包含的字元都不相同。

Tire樹的應用：

• 串的快速檢索

給出N個單片語成的熟詞表，以及一篇全用小寫英文書寫的文章，請你按最早出現的順序寫出所有不在熟詞表中的生詞。在這道題中，我們可以用陣列列舉，用雜湊，用字典樹，先把熟詞建一棵樹，然後讀入文章進行比較，這種方法效率是比較高的。

• “串”排序

給定N個互不相同的僅由一個單詞構成的英文名，讓你將他們按字典序從小到大輸出。用字典樹進行排序，採用陣列的方式建立字典樹，這棵樹的每個結點的所有兒子很顯然地按照其字母大小排序。對這棵樹進行先序遍歷即可。

• 最長公共字首

對所有串建立字典樹，對於兩個串的最長公共字首的長度即他們所在的結點的公共祖先個數，於是，問題就轉化為求公共祖先的問題。

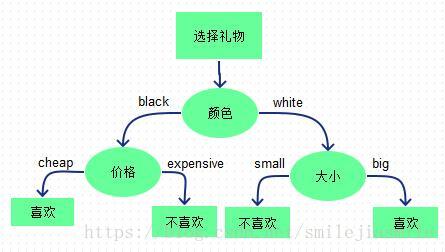
三、決策樹(利用資訊理論的熵依靠決策樹做決策選擇)

• 作為一個Coder,經常遇到敲if, else if, else,其實就就是決策樹的思想。只是這麼多條件，哪個條件特徵先做if，哪個條件特徵後做if比較優呢？怎麼準確定量選擇這個標準就是決策樹演算法的要做的事情。
• 資訊理論中熵的概念。熵度量了事物的不確定性，越不確定的事物，它的熵就越大。具體的，隨機變數X的熵的表示式如下：
• 單隨機變數 X 的熵

$H(X) = -\sum\limits_{i=1}^{n}p_i logp_i$

• 雙變數 X和Y 的聯合熵
  $H(X,Y) = -\sum\limits_{i=1}^{n}p(x_i,y_i)logp(x_i,y_i)$
• 條件熵的表示式H(X|Y)，條件熵類似於條件概率,它度量了我們的X在知道Y以後剩下的不確定性。表示式如下：

$H(X|Y) = -\sum\limits_{i=1}^{n}p(x_i,y_i)logp(x_i|y_i) = \sum\limits_{j=1}^{n}p(y_j)H(X|y_j)$

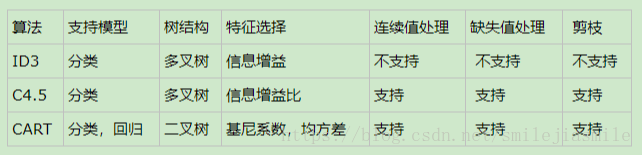
• 根據決策樹構建的過程，可以按照特徵選擇方式分成如下三種大類：

• 資訊增益(又稱為互資訊),定義為： H(X) - H(X|Y) ,記為I(X,Y)。
• 在決策樹 ID3 演算法中叫做資訊增益。ID3演算法就是用資訊增益來判斷當前節點應該用什麼特徵來構建決策樹。資訊增益大，則越適合用來分類。
• ID3 的缺點：
  • 沒有考慮連續特徵，比如長度，密度都是連續值，無法在ID3運用。
  • 取值比較多的特徵比取值少的特徵資訊增益大。
  • ID3演算法對於缺失值的情況沒有做考慮等
  • 沒有考慮過擬合的問題
• 於是提出了 C4.5
  • 對於使用資訊增益作為標準容易偏向於取值較多的特徵的問題。引入一個資訊增益率的變數Ir(X,Y)，它是資訊增益和特徵熵的比值。表示式如下：

$I_R(D,A) = \frac{I(A,D)}{H_A(D)}$

• C4.5 的缺點：
  • 決策樹演算法非常容易過擬合
  • C4.5生成的是多叉樹，在電腦科學中二叉樹往往運算效率更高。
  • C4.5只能用於分類，如果能將決策樹用於迴歸的話可以擴大它的使用範圍。
  • C4.5由於使用了熵模型，裡面有大量的耗時的對數運算,如果是連續值還有大量的排序運算。是否可以通過適當的降低結果準確性來簡化模型的運算強度。
• 前面兩種方式都是基於資訊理論的熵模型，有耗時的計算問題，CART分類樹演算法使用基尼係數來代替資訊增益比，基尼係數代表了模型的不純度，基尼係數越小，則不純度越低，特徵越好。這和資訊增益(比)是相反的。(其實就是加了一個負號，對比資訊熵的定義)
• 在分類問題中，假設有K個類別，第k個類別的概率為pk, 則基尼係數的表示式為：

$Gini(p) = \sum\limits_{k=1}^{K}p_k(1-p_k) = 1- \sum\limits_{k=1}^{K}p_k^2$

• 如果是二類分類問題，概率是p，則基尼係數簡化為：

$Gini(p) = 2p(1-p)$

四、梅克爾帕特里夏樹( Merkle Patricia Tree, MPT)

• MPT: 基於加密學的，自校驗防篡改的資料結構，用來儲存鍵值對關係。MPT是確定的。確定性是指同樣內容的鍵值，將被保證找到同樣的結果，有同樣的根雜湊。關於效率方面，對樹的插入，查詢，刪除的時間複雜度控制在O(log(n))。
• 前言：基數樹（Radix Tree）
• 在一個標準的基數樹裡，要儲存的資料，按下述所述：

[i0, i1, ... iN, value]

• 其中的i0到iN的表示一般是二進位制或十六進位制的格式的字母符號。value表示的是樹節點中儲存的最終值。每一個i0到iN槽位的值，要麼是NULL，要麼是指向另一個節點的指標（在當前這個場景中，儲存的是其它節點的雜湊值）。這樣我們就實現了一個簡單的鍵值對儲存。舉個例子來說，如果你想在這個基數樹中，找到鍵dog所對應的值。首先需要將dog轉換為比如ascii碼值（十六進位制表示是646f67）。然後按字母序形成一個逐層向下的樹。沿著字母組成的路徑，在樹的底部葉節點上，即找到dog對應的值。具體來說，首先找到儲存這個鍵值對資料的根節點，找到下一層的第6個節點，然後再往下一層，找到節點4，然後一層一層往下找，直到完成了路徑 root -> 6 -> 4 -> 6 -> f -> 6 -> 7。這樣你將最終找到值的對應節點。
• 基數樹的缺點:
  • 基數樹另一個主要的缺陷是低效。即使你只想存一個鍵值對，但其中的鍵長度有幾百字元長，那麼每個字元的那個層級你都需要大量的額外空間。每次查詢和刪除都會有上百個步驟。在這裡我們引入Patricia樹來解決這個問題。
• Patricia 樹
• Patricia樹，或稱Patricia trie，或 crit bit tree，壓縮字首樹，是一種更節省空間的Trie。對於基數樹的每個節點，如果該節點是唯一的兒子的話，就和父節點合併。

• Merkle 樹
• Merkle Tree，通常也被稱作Hash Tree，顧名思義，就是儲存hash值的一棵樹。Merkle樹的葉子是資料塊(例如，檔案或者檔案的集合)的hash值。非葉節點是其對應子節點串聯字串的hash。
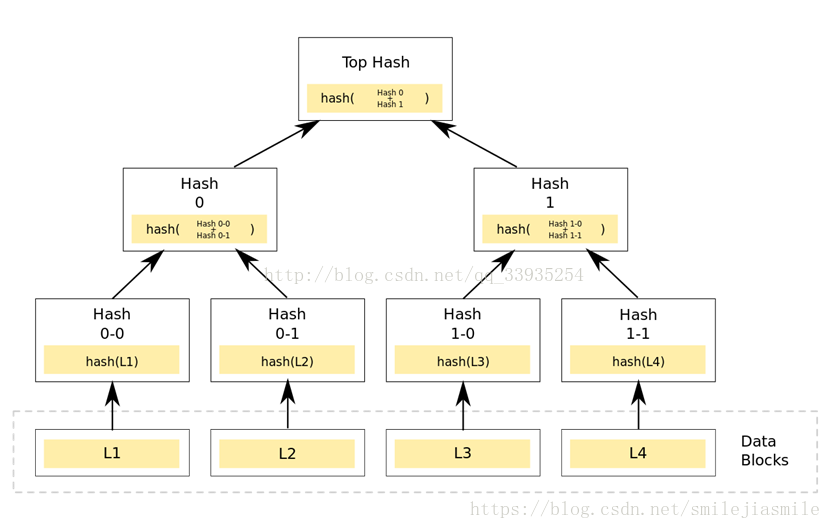
• Merkle Tree 由 Hash List演化而來：
• 在點對點網路中作資料傳輸的時候，會同時從多個機器上下載資料，而且很多機器可以認為是不穩定或者不可信的。為了校驗資料的完整性，更好的辦法是把大的檔案分割成小的資料塊（例如，把分割成2K為單位的資料塊）。這樣的好處是，如果小塊資料在傳輸過程中損壞了，那麼只要重新下載這一快資料就行了，不用重新下載整個檔案。
  怎麼確定小的資料塊沒有損壞哪？只需要為每個資料塊做Hash。BT下載的時候，在下載到真正資料之前，我們會先下載一個Hash列表。那麼問題又來了，怎麼確定這個Hash列表本身是正確的哪？答案是把每個小塊資料的Hash值拼到一起，然後對這個長字串在作一次Hash運算，這樣就得到Hash列表的根Hash(Top Hash or Root Hash)。下載資料的時候，首先從可信的資料來源得到正確的根Hash，就可以用它來校驗Hash列表了，然後通過校驗後的Hash列表校驗資料塊。

• Merkle Tree 可以看做Hash List的泛化（Hash List可以看作一種特殊的Merkle Tree，即樹高為2的多叉Merkle Tree。
• 在最底層，和雜湊列表一樣，我們把資料分成小的資料塊，有相應地雜湊和它對應。但是往上走，並不是直接去運算根雜湊，而是把相鄰的兩個雜湊合併成一個字串，然後運算這個字串的雜湊，這樣每兩個雜湊就結婚生子，得到了一個”子雜湊“。如果最底層的雜湊總數是單數，那到最後必然出現一個單身雜湊，這種情況就直接對它進行雜湊運算，所以也能得到它的子雜湊。於是往上推，依然是一樣的方式，可以得到數目更少的新一級雜湊，最終必然形成一棵倒掛的樹，到了樹根的這個位置，這一代就剩下一個根雜湊了，我們把它叫做 Merkle Root。

• 在p2p網路下載網路之前，先從可信的源獲得檔案的Merkle Tree樹根。一旦獲得了樹根，就可以從其他從不可信的源獲取Merkle tree。通過可信的樹根來檢查接受到的MerkleTree。如果Merkle Tree是損壞的或者虛假的，就從其他源獲得另一個Merkle Tree，直到獲得一個與可信樹根匹配的MerkleTree。
• Merkle Tree和HashList的主要區別是，可以直接下載並立即驗證 Merkle Tree的一個分支。因為可以將檔案切分成小的資料塊，這樣如果有一塊資料損壞，僅僅重新下載這個資料塊就行了。如果檔案非常大，那麼Merkle tree和Hash list都很到，但是Merkle tree可以一次下載一個分支，然後立即驗證這個分支，如果分支驗證通過，就可以下載資料了。而Hash list只有下載整個hash list才能驗證。
• MPT（Merkle Patricia Tree）樹
• MPT（Merkle Patricia Tree）就是這兩者混合的資料結構。
• MPT樹中的節點包括空節點、葉子節點、擴充套件節點和分支節點:
  • 空節點，簡單的表示空，在程式碼中是一個空串。
  • 葉子節點（leaf），表示為[key,value]的一個鍵值對，其中key是key的一種特殊十六進位制編碼，value是value的RLP編碼。
  • 擴充套件節點（extension），也是[key，value]的一個鍵值對，但是這裡的value是其他節點的hash值，這個hash可以被用來查詢資料庫中的節點。也就是說通過hash連結到其他節點。
  • 分支節點（branch），因為MPT樹中的key被編碼成一種特殊的16進位制的表示，再加上最後的value，所以分支節點是一個長度為17的list，前16個元素對應著key中的16個可能的十六進位制字元，如果有一個[key,value]對在這個分支節點終止，最後一個元素代表一個值，即分支節點既可以搜尋路徑的終止也可以是路徑的中間節點。
  • MPT 樹中另一個重要的概念是十六進位制字首(hex-prefix, HP)編碼，用來對key進行編碼。因為字母表是16進位制的，所以每個節點可能有16個孩子。因為有兩種[key,value]節點(葉節點和擴充套件節點)，引進一種特殊的終止符標識來標識key所對應的是值是真實的值，還是其他節點的hash。如果終止符標記被開啟，那麼key對應的是葉節點，對應的值是真實的value。如果終止符標記被關閉，那麼值就是用於在資料塊中查詢對應的節點的hash。

五、電腦科學中的樹結構