[C++]二分查詢法
引用:https://baike.baidu.com/item/%E4%BA%8C%E5%88%86%E6%B3%95/1364267?fr=aladdin
二分法
對於區間
上連續不斷且
的函式
,通過不斷地把函式
的零點所在的區間一分為二,使區間的兩個端點逐步逼近零點,進而得到零點近似值的方法叫二分法。
定義
二分法(Bisection method) 即一分為二的方法. 設
為R的閉區間. 逐次二分法就是造出如下的區間序列
,
,且對任一自然數
,
或者等於
,或者等於
,其中
表示
的中點。
典型演算法
演算法:當資料量很大適宜採用該方法。採用二分法查詢時,資料需是排好序的。
基本思想:假設資料是按升序排序的,對於給定值
,從序列的中間位置k開始比較,
如果當前位置
值等於
,則查詢成功;
若
小於當前位置值
,則在數列的前半段中查詢,
;
若
大於當前位置值
,則在數列的後半段中繼續查詢
,
直到找到為止,時間複雜度:
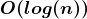
求法
給定精確度
,用二分法求函式
零點近似值的步驟如下:
1 確定區間
,驗證
,給定精確度
.
2 求區間
的中點
.
3 計算
.
(1) 若
,則
就是函式的零點;
(2) 若
,則令
;
(3) 若
,則令
.
(4) 判斷是否達到精確度
:即若
,則得到零點近似值
(或
),否則重複2-4.
例題
Oj Url:http://noi.openjudge.cn/ch0111/02/
http://noi.openjudge.cn/ch0111/01/
01:二分法求函式的零點
總時間限制: 1000ms
記憶體限制: 65536kB
描述
有函式:
已知
,
且方程在區間
有且只有一個根,請用二分法求出該根。
輸入 無
輸出 該方程在區間
中的根。要求四捨五入到小數點後6位。
樣例輸入 無
樣例輸出 不提供
程式程式碼
#include <iostream>
#include <iomanip>
#include <cmath>
typedef double db;
inline bool determine(const db mid) {
db f = pow(mid, 5) - 15.0 * pow(mid, 4) + 85.0 * pow(mid, 3) - 225.0 * pow(mid, 2) + 274.0 * mid - 121.0;
return f > 0.0;
};
int main(int argc, char *argv[]) {
std::ios::sync_with_stdio(false);
db left = 1.5, right = 2.4, mid;
while (right - left > 1e-8) {
mid = left + (right - left) / 2.0;
if (determine(mid)) left = mid;
else right = mid;
};
std::cout << std::fixed << std::setprecision(6) << mid << std::endl;
return 0;
}; 02:查詢最接近的元素
總時間限制: 1000ms
記憶體限制: 65536kB
描述
在一個非降序列中,查詢與給定值最接近的元素。
輸入
第一行包含一個整數
,為非降序列長度。
。
第二行包含個整數,為非降序列各元素。所有元素的大小均在
之間。
第三行包含一個整數,為要詢問的給定值個數。
。
接下來m行,每行一個整數,為要詢問最接近元素的給定值。所有給定值的大小均在之間。
輸出
行,每行一個整數,為最接近相應給定值的元素值,保持輸入順序。若有多個值滿足條件,輸出最小的一個。
樣例輸入
3 2 5 8 2 10 5樣例輸出
8 5
程式程式碼
#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
typedef long long ll;
const int INF = 0x3ffffff;
const int MAX_SIZE = 1000001;
int array[MAX_SIZE] = {};
template <typename _Tp>
inline void quicksort(_Tp *arr, int start, int end) {
int i = start, j = end; _Tp pivot = arr[start];
if (i >= j) return;
while (i != j) {
while (i < j && arr[j] > pivot) --j;
while (i < j && arr[i] < pivot) ++i;
if (i < j) swap(arr[i], arr[j]);
};
swap(arr[i], arr[start]);
quicksort(arr, start, i - 1);
quicksort(arr, i + 1, end);
};
int main(int argc, char *argv[]) {
int n; cin >> n;
for (int i = 0; i < n; ++i) scanf("%d", array + i);
int m; cin >> m;
while (m--) {
int bf, answer, left = 0, mid, right = n - 1; cin >> bf;
if (bf <= array[0]) {cout << array[0] << endl; continue;};
if (bf >= array[n - 1]) {cout << array[n - 1] << endl; continue;};
while (left <= right) {
mid = left + (right - left) / 2;
if(array[mid] <= bf) left = mid + 1;
else right = mid - 1;
};
if (abs(array[left] - bf) < abs(array[right] - bf)) answer = left;
else answer = right;
cout << array[answer] << endl;
};
return 0;
};