邏輯迴歸

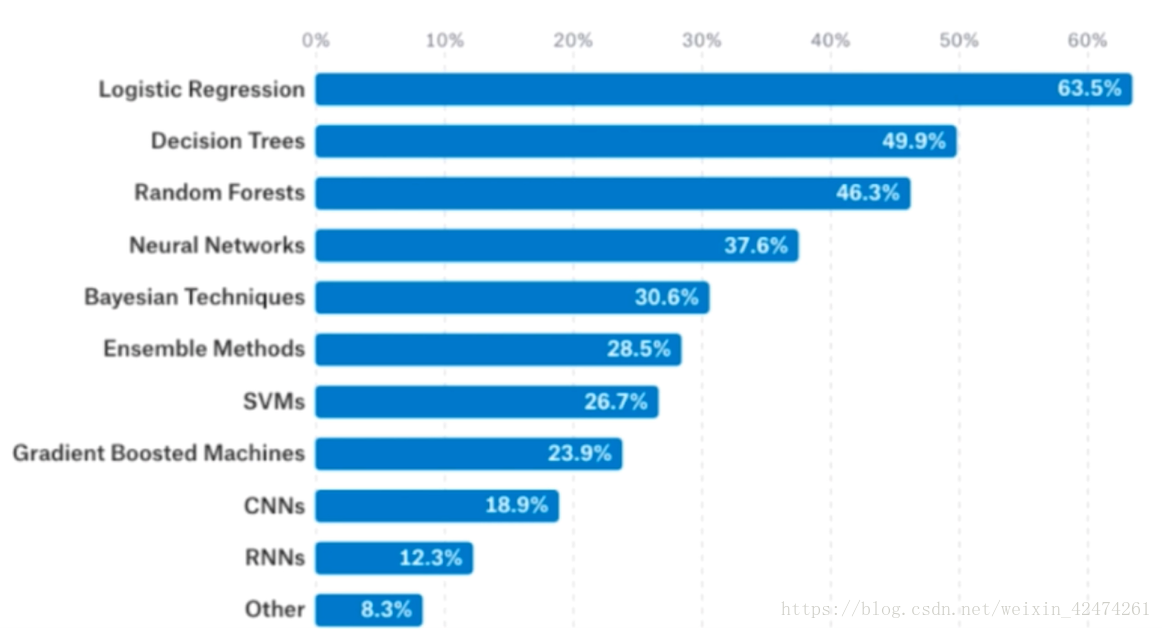
據統計，在kaggle上使用邏輯迴歸解決問題的比例是非常大的，並且超出第二名決策樹20%多，說明邏輯迴歸普適性較強，而神經網路相關演算法對資料的要求比較高。

什麼是邏輯迴歸

聽起來邏輯迴歸是一個迴歸演算法，但是事實上它解決的卻是分類問題。它的原理是將樣本的特徵與樣本發生的概率練習起來。
$P=f($

x ) P = f(x)
根據概率值P進行分類
$P=\{\begin{array}{c}1\end{array}$

0.5 ≤ P < 1

0 0 ≤ P < 0.5 P = \begin{cases} 1 & 0.5 \leq P < 1 \\0 & 0 \leq P < 0.5 \end{cases}
邏輯迴歸本身只可以解決二分類問題，可以通過改進解決多分類問題。
線上性迴歸中通過 $f(x)$的計算，根據樣本值計算出 $y$值，表示為
$y = \Theta^T X_b$
其中 $y = f(x)$的值域在 $(-\infty,+\infty)之間，而邏輯迴歸取值範圍在$[0, 1]之間。因此直接使用線性迴歸的方式來表達邏輯迴歸的值不太合適。
解決方案是通過 $\sigma$方法，來將 $y$的取值加以限定，那麼就的到了下面的式子
$p = \sigma(\Theta^T X_b)$
我們將 $\sigma(t)$設定成這樣一個函式
$\sigma(t)= \frac{1}{1+e^{-t}}$
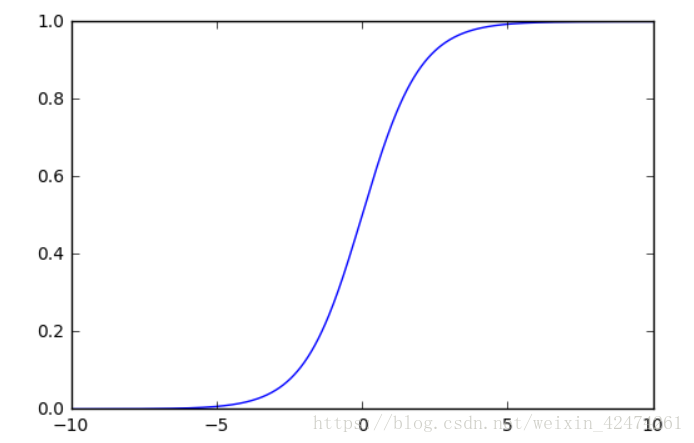
因為這個Sigmoid函式的曲線如下圖1：

通過在 $(0,0)$處建立直角座標系，可以分析得出，當 $x\rightarrow-\infty$時， $y$值無限趨近於0，當 $x\rightarrow\infty$時， $y$值無限趨近於1。
則事件發生的概率可以表示為：
$\sigma(t)= \frac{1}{1+e^{-\Theta^T X_b}}$
例子：病人資料預測腫瘤是良性還是惡性
每來一組新的資料，通過Sigmoid函式的計算把 $y$值來與0.5比較，當概率值 $y > 0.5$時，我們就預測患者腫瘤是惡性的，如果 $y < 0.5$，我們就預測患者的腫瘤是良性的。
問題：
如何找到引數theta，使用這樣的方式，可以最大程度獲得樣本資料X對應的分類輸出y

邏輯迴歸的損失函式

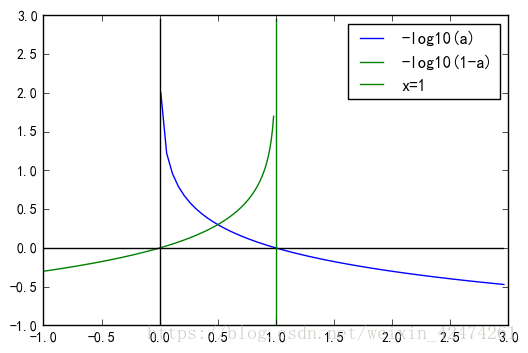
首先它的損失函式趨勢如下
$cost = \begin{cases} 如果y=1,p越小，cost越大 \\如果y=0,p越大，cost越大\end{cases}$
則可以找到滿足該趨勢的如下函式
$cost = \begin{cases}-\log(p) & if & y = 1 \\-\log(1-p)& if &y=0 \end{cases}$

將cost損失函式整合到一起，用一個式子來表達，可得到
$cost = -yln(p)-(1-y)ln(1-p)$
m個樣本求平均
$J(\theta) = -\frac{1}{m} \sum_{i=1}^{m}{y^{(i)}ln(p^{(i)})+(1-y^{(i)})ln(1-p^{(i)})}$
$p^{(i)}=\sigma(\Theta X_b^{(i)})= \frac{1}{1+e^{-\Theta X_b^{(i)}}}$
接