邏輯迴歸的特點

邏輯迴歸的用途

第一用來預測，第二尋找因變數的影響因素。

邏輯迴歸的適用範圍

資料型別

邏輯迴歸的優點

原理的相對簡單，可解釋性強等優點,它還可以作為眾多整合演算法以及深度學習的基本組成單位 Logistic迴歸分析報告結果解讀分析

邏輯迴歸的侷限性

邏輯迴歸模型的引入(從線性迴歸到Logistic迴歸)

廣義線性模型 這一家族中模型的形式基本一致，不同的是因變數不同

• 如果是連續的，就是線性迴歸
• 如果是二項分佈，就是logistic迴歸
• 如果是poisson分佈，就是poisson迴歸
• 如果負二項分佈，就是負二項迴歸

線性迴歸和Logistic迴歸都是廣義線性模型的特例。 假設有一個因變數$y$

y和一組自變數$x_1, x_2, x_3, ... , x_n$，其中$y$為連續變數，我們可以擬合一個線性方程： $y =w_0 +w_1*x_1 +w_2*x_2 +w_3*x_3 +\cdots+w_n*x_n-----(1)$ 並通過最小二乘法估計各個$w$係數的值。 如果$y$為二分類變數，只能取值0或1，那麼線性迴歸方程就會遇到困難: 方程右側是一個連續的值，取值為負無窮到正無窮，而左側只能取值[0,1]，無法對應。為了繼續使用線性迴歸的思想，統計學家想到了一個變換方法，就是將方程右邊的取值變換為[0,1]。最後選中了sigmoid函式：$s$

(x)=11+e−xs(x)=\frac{1}{1+e^{-x}}，sigmoid函式曲線如下： Sigmoid函式在兩側能很快收斂至0和1，此特性很適合邏輯迴歸的需要，將方程(1)右側代入sigmoid函式有

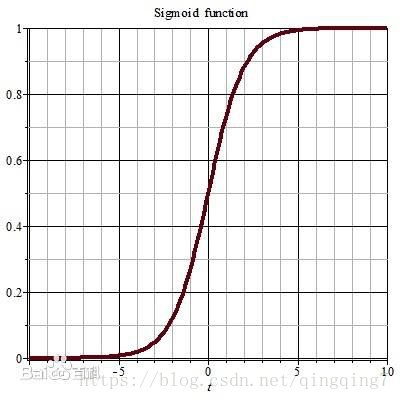
$y=\frac{1}{1+e^{-(w_0 +w_1*x_1 +w_2*x_2 +w_3*x_3 +...+w_n*x_n)}}----(2)$ 按照(2)式，對於任意取值的x,因變數y的取值範圍都為(0~1)；但是在分類模型中，y的取值只能是1或0；如果令$y$

=py=p，我們還需要做一些規定，比如當$p\geq 0.5$時，y的取值為1；當$p< 0.5$時,y的取值為0；當我們通過一定的方法，得到一組合適的引數$w_0 、w_1、w_2、w_3、...、w_n$,那麼只要樣本代入(2)式，根據計算出來p值的大小就可以對的樣本的類別進行判定；此時結果p就相當於y取1的概率，與此對應的，y取0的概率為$1-p$。sigmoid函式好處在於在x=0的兩側能很快收斂至0和1，保證能夠匹配大部分樣本的類別。 那麼如何來求解這樣一組引數呢？ 引數的最優解應該要滿足這樣的要求：最優引數應該讓儘可能多的樣本在給定的屬性值下其類別儘可能呈現其本來的樣子；也就是對於全體樣本，在給定的屬性值和類別取值下，通過(2)式計算得到的類別取值的聯合概率應該最大。 這裡我們就引出了邏輯迴歸模型引數求解的目標函式。

補充知識：

優勢$\Omega$ 優勢，是事件發生與不發生概率之比，用符號$\Omega$來表示。 $\Omega=\frac{p}{1-p}=e^{(w_0 +w_1*x_1 +w_2*x_2 +w_3*x_3 +...+w_n*x_n)}$ $\Omega$是$p$的單調函式，保證了$\Omega$和p增長的一致性，$Ω$的取捨範圍是$(0,+\infty)$； 如果再對$\Omega$取對數，則有 $ln\Omega=ln\frac{p}{1-p}=w_0 +w_1*x_1 +w_2*x_2 +w_3*x_3 +...+w_n*x_n$ $logit$變換 上述兩步變換稱為$logit$變換，$ln\Omega$稱為$logitP$，$logitP$的取捨範圍$(-\infty,+\infty)$，與一般線性迴歸模型吻合，同時與p之間保值單調一致性。這樣我們完成了從一般線性迴歸到邏輯迴歸的轉換。 $logit$變換在後面的引數求解中還會用到，可以簡化推導過程。

邏輯迴歸模型的引數估計

設$y$是0-1型變數，$(x_1,x_2,\dots,x_p)$是與$y$相關的確定性變數即特徵變數；n組觀測資料，記為$(x_{i1},x_{i2},\dots,x_{ip};y_i)(i=1,2,\dots,n)$,其中$y_i$是取值為0或1的隨機變數。 $y_i$是均值為$p_i$的0-1分佈，概率函式為$P(y_i=1)=p_i$；$P(y_i=0)=1-p_i$，我們可以將概率函式合寫為$P(y_i)=p_i^{y_i}(1-p_i)^{1-y_i};i=1,2,\dots,n;y_i=0,1$；於是$(y_1,y_2,\dots,y_n)$

相關推薦