邏輯迴歸

對邏輯迴歸的理解：對線性迴歸的假設函式的 f(x) 又套上了一層sigmoid函式，即g(f(x)).

然後sigmoid函式是長這樣的：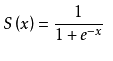

它的影象長這樣：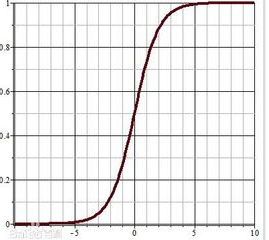

對於線性迴歸得到的結果，再經過一層sigmoid函式，以x=0為界限，左邊為0，右邊為1，邏輯迴歸就是這樣一個二分類的演算法。

那我們再從數學的角度去看一下它的推導過程，在此之前，要知道sigmoid的導函式很特殊，長這樣的，感受一下：

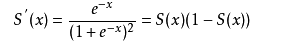
然後是推導過程：

梯度下降演算法的原理在之前的文章中多次提及，這裡不再記錄，就是一個凸函式的求解過程。

softmax函式

 softmax函式是邏輯迴歸的一般化，邏輯迴歸只能夠處理二分類，而softmax能夠處理多酚類，它的公式：

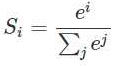
sklearn中常用引數：

lr = LogisticRegressionCV(fit_intercept=True, 
                          multi_class='multinomial', penalty='l2', solver='lbfgs')
## penalty: 過擬合解決引數,l1或者l2

## solver: 引數優化方式
### 當penalty為l1的時候，引數只能是：liblinear(座標軸下降法)；
### 當penalty為l2的時候，引數可以是：lbfgs(擬牛頓法)、newton-cg(牛頓法變種)

## multi_class: 分類方式引數；引數可選: ovr(預設)、multinomial；這兩種方式在二元分類問題中，效果是一樣的；在多元分類問題中，效果不一樣
### ovr: one-vs-rest， 對於多元分類的問題，先將其看做二元分類，分類完成後，再迭代對其中一類繼續進行二元分類
### multinomial: many-vs-many（MVM）,對於多元分類問題，如果模型有T類，我們每次在所有的T類樣本里面選擇兩類樣本出來，
#### 不妨記為T1類和T2類，把所有的輸出為T1和T2的樣本放在一起，把T1作為正例，T2作為負例，
#### 進行二元邏輯迴歸，得到模型引數。我們一共需要T(T-1)/2次分類

## class_weight: 特徵權重引數

### Softmax演算法相對於Logistic演算法來講，在sklearn中體現的程式碼形式來講，主要只是引數的不同而已
## Logistic演算法迴歸(二分類): 使用的是ovr；如果是softmax迴歸，建議使用multinomial