[Luogu P2414] [BZOJ 2434] [NOI2011]阿狸的打字機
洛谷傳送門
BZOJ傳送門
題目背景
阿狸喜歡收藏各種稀奇古怪的東西,最近他淘到一臺老式的打字機。
題目描述
打字機上只有 個按鍵,分別印有 個小寫英文字母和 、 兩個字母。經阿狸研究發現,這個打字機是這樣工作的:
- 輸入小寫字母,打字機的一個凹槽中會加入這個字母(這個字母加在凹槽的最後)。
- 按一下印有 的按鍵,打字機凹槽中最後一個字母會消失。
- 按一下印有 的按鍵,打字機會在紙上打印出凹槽中現有的所有字母並換行,但凹槽中的字母不會消失。
例如,阿狸輸入aPaPBbP,紙上被列印的字元如下:
a aa ab 我們把紙上打印出來的字串從
開始順序編號,一直到
。打字機有一個非常有趣的功能,在打字機中暗藏一個帶數字的小鍵盤,在小鍵盤上輸入兩個數
(其中
),打字機會顯示第
個列印的字串在第
個列印的字串中出現了多少次。
阿狸發現了這個功能以後很興奮,他想寫個程式完成同樣的功能,你能幫助他麼?
輸入輸出格式
輸入格式:
輸入的第一行包含一個字串,按阿狸的輸入順序給出所有阿狸輸入的字元。
第二行包含一個整數 ,表示詢問個數。
接下來 行描述所有由小鍵盤輸入的詢問。其中第 行包含兩個整數 ,表示第 個詢問為 。
輸出格式:
輸出 行,其中第i行包含一個整數,表示第i個詢問的答案。
輸入輸出樣例
輸入樣例#1:
aPaPBbP
3
1 2
1 3
2 3
輸出樣例#1:
2
1
0
說明
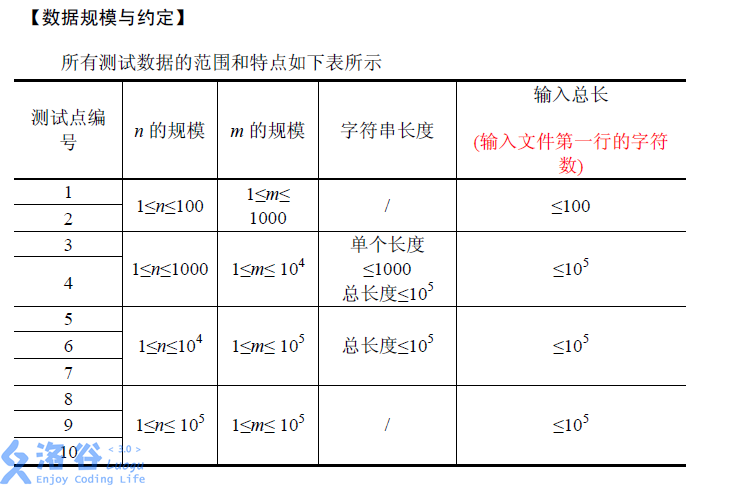
資料範圍:
對於 的資料, ,第一行總長度 。
解題分析
自動機好題。 建自動機什麼的都好說, 只是額外維護一個父親節點表示從其轉移過來的即可完成回退操作。
問題在於如果我們每次暴力匹配複雜度會變成 的。 如何優化?
考慮我們是如何暴力的: 對 串建立 自動機, 將 串依次插入, 暴力跳 , 看是否能到達 串的終止位置。 我們發現, 只要插入的字元在 樹上在 串終止位置的子樹中, 就會產生貢獻。
這樣就好做了:我們離線詢問, 整顆 樹, 每到達一個節點就將其在 樹上的 序處的貢獻 。 如果到達了某個串的終止節點, 就回答其作為 串的所有詢問(直接查詢 在 樹中的子樹貢獻之和)。
程式碼如下:
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <cctype>
#include <algorithm>
#include <queue>
#include <vector>
#define R register
#define IN inline
#define W while
#define gc getchar()
#define lbt(i) ((i) & (-(i)))
#define MX 100500
template <class T>
IN void in(T &x)
{
x = 0; R char c = gc;
for (; !isdigit(c); c = gc);
for (; isdigit(c); c = gc)
x = (x << 1) + (x << 3) + c - 48;
}
int cnt, m, tot, dfn, root;
int son[MX][26], fat[MX], fail[MX], ed[MX], lb[MX], rb[MX], head[MX], tree[MX], p[MX], ans[MX];
char buf[MX];
struct INFO {int tar, tim;};
std::vector <int> to[MX];
std::vector <INFO> que[MX];
std::queue <int> q;
IN void add(R int pos, R int del) {for (; pos <= cnt + 1; pos += lbt(pos)) tree[pos] += del;}
IN int query(R int pos) {int ret = 0; for (; pos; pos -= lbt(pos)) ret += tree[pos]; return ret;}
IN void insert(char *str)
{
R int now = root, len = std::strlen(str), id;
for (R int i = 0; i < len; ++i)
{
if (str[i] == 'P') ed[now] = ++tot, p[tot] = now;
else if (str[i] == 'B') now = fat[now];
else
{
id = str[i] - 'a';
if (!son[now][id]) son[now][id] = ++cnt, fat[son[now][id]] = now;
now = son[now][id];
}
}
}
void build()
{
R int now, cur; fail[0] = -1;
for (R int i = 0; i < 26; ++i) if (son[root][i]) q.push(son[root][i]), to[root].push_back(son[root][i]);
W (!q.empty())
{
now = q.front(); q.pop();
for (R int i = 0; i < 26; ++i)
{
if (son[now][i])
{
cur = fail[now];
W ((~fail[cur]) && (!son[cur][i])) cur = fail[cur];
fail[son[now][i]] = son[cur][i];
q.push(son[now][i]); to[fail[son[now][i]]].push_back(son[now][i]);
}
}
}
}
void DFS1(R int now)
{
lb[now] = ++dfn;
for (R int i = to[now].size() - 1; ~i; --i) DFS1(to[now][i]);
rb[now] = dfn;
}
void DFS2(R int now)
{
add(lb[now], 1);
if (ed[now])
{
INFO cur;
for (R int i = que[now].size() - 1; ~i; --i)
{
cur = que[now][i];
ans[cur.tim] = query(rb[p[cur.tar]]) - query(lb[p[cur.tar]] - 1);
}
}
for (R int i = 0; i < 26; ++i)
if (son[now][i]) DFS2(son[now][i]);
add(lb[now], -1);
}
int main(void)
{
int x, y;
scanf("%s", buf); insert(buf);
in(m);
for (R int i = 1; i <= m; ++i)
{
in(x), in(y);
que[p[y]].push_back({x, i});
}
build(); DFS1(0); DFS2(0);
for (R int i = 1; i <= m; ++i) printf("%d\n", ans[i]);
}
