題目連結：https://vjudge.net/problem/HDU-1317

題目描述：

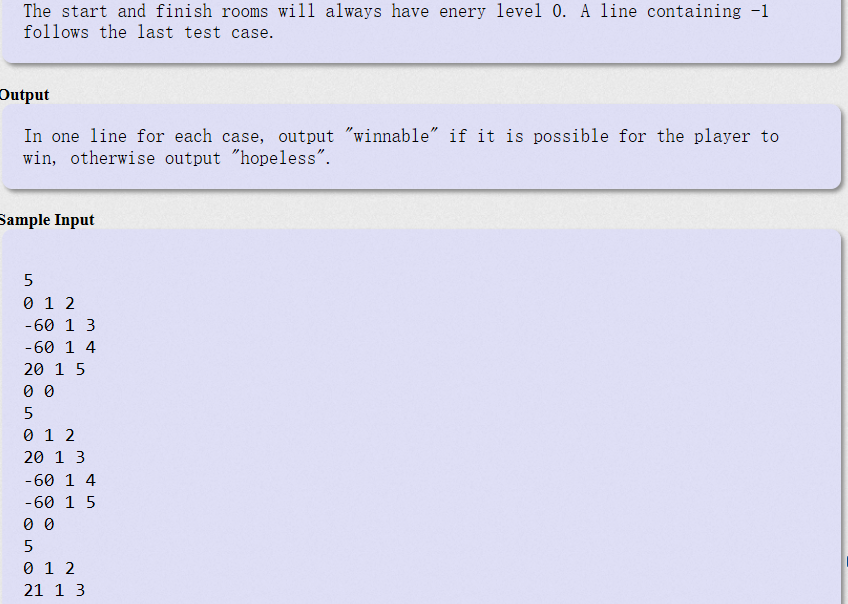
　　題意：玩家起始有100個能量點，剛開始在起始房間中，每個房間外有一條單向的路徑通往其他房間（一個房間可能通往多個房間），具體通往哪些房間可以檢視房間門口的房間列表。每次玩家進入一個房間，他的能量值會更新成 當前自身能量值+房間能量值（重點是房間的能量值可能為負值）。玩家想要終止遊戲的話，要麼是能夠進入到終點房間，要麼是因能量耗盡而累死。需要我們判斷玩家能否進入到終點房間。

　　Floyd演算法（Floyd-Warshall algorithm）又稱為弗洛伊德演算法、插點法，是解決給定的加權圖中頂點間的最短路徑的一種演算法，可以正確處理

　　因為此題中存在負權值，因此用Floyd最短路來解決。

　　思路：首先我們需要檢查是否存在這樣的路從1到達N，如果不存在，直接輸出hopeless。我們可以利用floyd演算法去檢查。Floyd-Warshall演算法是一種在具有正或負邊緣權重（但沒有負週期）的加權圖中找到最短路徑的演算法。因為題中可能會出現負週期——行成環路，可以無限增加能量值。但是可以用於檢查1到N是否連通。然後我們再使用Bellman演算法，如果鬆弛N-1次後，任然存在更新。說明圖中存在負週期，說明能量可以無限疊加，檢查環路的點是否與N連通就行了。如果不存在負週期，則檢查到達N的能量是否大於0。轉載自博文：

程式碼實現：

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int N,M;
const int MAXN =105;
const int INF = 0x3f3f3f3f;
/*    d陣列表示到達i房間的最大的能量值；
    p陣列表示每個房間的能量值；
    G陣列存圖。G[i][j]=1，表示i到j有1條通路。
    E陣列存邊。
 
*/
struct edge{
    int from,to;
}E[MAXN*MAXN];
int d[MAXN],P[MAXN];
int G[MAXN][MAXN];
bool floyd()//判斷是否房間之間是可達的，如不可達，則輸出hopeless
{
    for(int k=1;k<=N;k++)
        for(int i=1;i<=N;i++)
            for(int j=1;j<=N;j++)
                if(G[i][k]&&G[k][j])
                    G[i][j]=1;
    return G[1][N];
}

bool bellman(){
    fill(d,d+MAXN,-INF);
    d[1]=100;//初始值為100
    for(int i=1;i<N;i++)
    {
        bool flag=false;
        for(int j=0;j<M;j++){
            if(d[E[j].to] < d[E[j].from]+P[E[j].to] && d[E[j].from]+P[E[j].to]>0){
                flag=true;
                d[E[j].to]=d[E[j].from]+P[E[j].to];
            }
        }
        if(!flag) break;
    }
    for(int j=0;j<M;j++){
        if(d[E[j].to] < d[E[j].from]+P[E[j].to] && d[E[j].from]+P[E[j].to]>0){
            d[E[j].to]=d[E[j].from]+P[E[j].to];
            if(G[E[j].to][N]){
                return true;
            }
        }
    }
    return d[N]>0;
}

int main(){
    while(~scanf("%d",&N)&&(N!=-1)){
        memset(G,0,sizeof(G));
        memset(E,0,sizeof(E));
        memset(P,0,sizeof(P));
        M=0;
        int con;//記錄連線多少扇門
        for(int i=1;i<=N;i++){
            scanf("%d%d",&P[i],&con);
            for(int j=1;j<=con;j++){
                int tmp;scanf("%d",&tmp);
                E[M++]=(edge){i,tmp};
                G[i][tmp]=1;//說明從門i到門tmp是可達的
            }
        }
        if(!floyd()){
            printf("hopeless\n");
            continue;
        }
        if(bellman()){
            printf("winnable\n");
        }else{
            printf("hopeless\n");
        }
    }
    return 0;
}