二叉排序樹之查詢演算法
1.二叉排序樹的定義與描述
二叉排序樹又稱為二叉查詢樹,它是一種特殊的二叉樹。
定義:二叉排序樹是一顆空樹或者是具有一下性質的二叉樹。
1)若它的左子樹非空,則左子樹上所有的結點值均小於根結點的值。
2)若它的右子樹非空,則右子樹上所有的結點的值均大於(或等於)根結點的值。
3)它的左右子樹也分別是二叉排序樹。
2.資料結構
3.二叉排序樹的建立
可以將樹結點逐個插入到二叉排序樹(一開始可以是一顆空樹)中,只要保證插入後,依然滿足二叉排序樹的特點,就可以建立一個二叉排序樹。
設樹結點的關鍵字值為key
演算法思想:
1)若二叉排序樹是空樹,則將key結點成為二叉排序樹的根結點。
2)若二叉排序樹非空樹,則將key與二叉排序樹的根進行比較:
a.如果key的值等於根結點的值,則停止插入。
b.如果key的值小於根結點的值,則將key所在結點插入左子樹。
c.如果key的值大於根結點的值,則將key所在結點插入右子樹。
演算法實現:
4.二叉排序樹的查詢
因為二叉排序樹是可以看作是一個有序表,所以其查詢過程和折半查詢類似。
演算法思想:
首先將待查關鍵字key與根節點關鍵字t進行比較:
a.如果key = t, 則返回根節點指標。
b.如果key < t,則進一步查詢左子書。
c.如果key > t,則進一步查詢右子樹。
1)遞迴演算法實現:
/*在根指標bst所指二叉排序樹中,遞迴查詢某關鍵字等於key的元素,若查詢成功,返回指向該元素結點指標,否則返回空指*/
BSTree SearchBST(BSTree bst, KeyType key) {
if
return NULL;
else
if (bst->key== key)
return bst;/*查詢成功* /
else {
if
return SearchBST(bst->lchild, key);/*在左子樹繼續查詢*/
else
return SearchBST(bst->rchild, key);/*在右子樹繼續查詢*/
}
}
2)非遞迴實現
BSTree SearchBST(BSTree bst, KeyType key)
/*在根指標bst所指二叉排序樹bst上,查詢關鍵字等於key的結點,若查詢成功,返回指向該元素結點指標,否則返回空指標*/
{
BSTree q;
q=bst;
while(q)
{
if (q->key == key)
return q; /*查詢成功*/
if (q->key > key)
q=q->lchild; /*在左子樹中查詢*/
else
q=q->rchild; /*在右子樹中查詢*/
}
return NULL; /*查詢失敗*/
}完整程式碼描述:
#include <stdio.h>
#include <stdlib.h>
#define ENDKEY 0
typedef int KeyType;
typedef struct node
{
KeyType key ; /*關鍵字的值*/
struct node *lchild,*rchild;/*左右指標*/
}BSTNode, *BSTree;
void InsertBST(BSTree *bst, KeyType key)
/*若在二叉排序樹中不存在關鍵字等於key的元素,插入該元素*/
{
BSTree s;
if (*bst == NULL)/*遞迴結束條件*/
{
s=(BSTree)malloc(sizeof(BSTNode));/*申請新的結點s*/
s-> key=key;
s->lchild=NULL;
s->rchild=NULL;
*bst=s;
}
else
if (key < (*bst)->key)
InsertBST(&((*bst)->lchild), key);/*將s插入左子樹*/
else
if (key > (*bst)->key)
InsertBST(&((*bst)->rchild), key); /*將s插入右子樹*/
}
void CreateBST(BSTree *bst)
/*從鍵盤輸入元素的值,建立相應的二叉排序樹*/
{
KeyType key;
*bst=NULL;
scanf("%d", &key);
while (key!=ENDKEY) /*ENDKEY為自定義常量*/
{
InsertBST(bst, key);
scanf("%d", &key);
}
}
void PreOrder(BSTree root)
/*先序遍歷二叉樹, root為指向二叉樹根結點的指標*/
{
if (root!=NULL)
{
printf("%d ",root->key); /*輸出結點*/
PreOrder(root->lchild); /*先序遍歷左子樹*/
PreOrder(root->rchild); /*先序遍歷右子樹*/
}
}
/*
BSTree SearchBST(BSTree bst, KeyType key)
/ *在根指標bst所指二叉排序樹中,遞迴查詢某關鍵字等於key的元素,若查詢成功,返回指向該元素結點指標,否則返回空指標* /
{
if (!bst)
return NULL;
else
if (bst->key == key)
return bst;/ *查詢成功* /
else
if (bst->key > key)
return SearchBST(bst->lchild, key);/ *在左子樹繼續查詢* /
else
return SearchBST(bst->rchild, key);/ *在右子樹繼續查詢* /
}*/
BSTree SearchBST(BSTree bst, KeyType key)
/*在根指標bst所指二叉排序樹bst上,查詢關鍵字等於key的結點,若查詢成功,返回指向該元素結點指標,否則返回空指標*/
{
BSTree q;
q=bst;
while(q)
{
if (q->key == key)
return q; /*查詢成功*/
if (q->key > key)
q=q->lchild; /*在左子樹中查詢*/
else
q=q->rchild; /*在右子樹中查詢*/
}
return NULL; /*查詢失敗*/
}/*SearchBST*/
BSTNode * DelBST(BSTree t, KeyType k) /*在二叉排序樹t中刪去關鍵字為k的結點*/
{
BSTNode *p, *f,*s ,*q;
p=t;
f=NULL;
while(p) /*查詢關鍵字為k的待刪結點p*/
{
if(p->key==k ) break; /*找到則跳出迴圈*/
f=p; /*f指向p結點的雙親結點*/
if(p->key>k)
p=p->lchild;
else
p=p->rchild;
}
if(p==NULL) return t; /*若找不到,返回原來的二叉排序樹*/
if(p->lchild==NULL) /*p無左子樹*/
{
if(f==NULL)
t=p->rchild; /*p是原二叉排序樹的根*/
else
if(f->lchild==p) /*p是f的左孩子*/
f->lchild=p->rchild ; /*將p的右子樹鏈到f的左鏈上*/
else /*p是f的右孩子*/
f->rchild=p->rchild ; /*將p的右子樹鏈到f的右鏈上*/
free(p); /*釋放被刪除的結點p*/
}
else /*p有左子樹*/
{
q=p;
s=p->lchild;
while(s->rchild) /*在p的左子樹中查詢最右下結點*/
{
q=s;
s=s->rchild;
}
if(q==p)
q->lchild=s->lchild ; /*將s的左子樹鏈到q上*/
else
q->rchild=s->lchild;
p->key=s->key; /*將s的值賦給p*/
free(s);
}
return t;
} /*DelBST*/
void main()
{
BSTree T;
int k;
BSTree result;
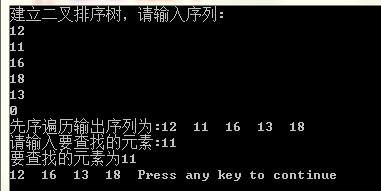
printf("建立二叉排序樹,請輸入序列:\n");
CreateBST(&T);
printf("先序遍歷輸出序列為:");
PreOrder(T);
printf("\n請輸入要查詢的元素:");
fflush(stdin);
scanf("%d",&k);
result = SearchBST(T,k);
if (result != NULL)
printf("要查詢的元素為%d\n",result->key);
else
printf("未找到!\n");
result = DelBST(T,k);
PreOrder(result);
}執行結果圖: