KMP演算法是由三個科學家(kmp分別是他們名字的首字母)創造出來的一種字串匹配演算法.

所解決的問題:

　　求文字字串text內尋找第一次出現字串s的下標,若未出現返回-1。

　　例如

　　　　text : "adesceqwdasdfagf";

　　　　s : "sce";

　　　　return : 3;

　　常規解法 :

　　　　　/**
	 * 常規演算法
	 * 將以i為頭的text子串與s串比對
	 * 如若比對失敗則i++;繼續比對i子串與s。
	 * @param text
	 * @param s
	 * @return
	 */
	public static int strStr(String text, String s) {
		if (text == null || s == null || s.length() == 0 || text.length() < s.length()) {
			return -1;
		}
		int i = 0, j = 0;
		while (i + j < text.length() && j < s.length()) {
			if (text.charAt(i + j) == s.charAt(j)) {
				j++;
			}else {
				i++; j = 0;
			}
		}return j != s.length() ? -1 : i - j;
	}

　　　　由於常規解法並不複雜並且,在註釋上已經有概括講解,所以我們就不再贅述了。

　　　　那麼是否有更好一些的辦法省去一些沒有必要的操作以達到優化演算法的目的呢？

　　　　以下是我們考慮的一個例子:

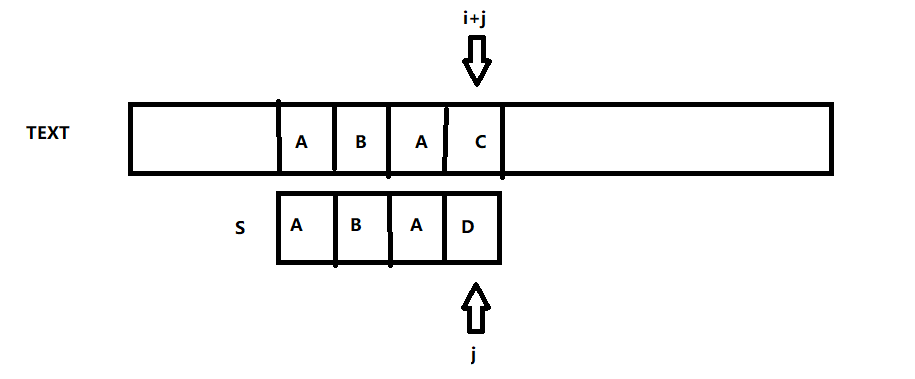
　　　　例如上圖的例子,當前匹配的是以A開頭的子串與s進行比對,而C,D不同,故而按照常規演算法來說應該是i++,也就是i會到達B,j = 0,然後開始新一輪的比對,即TEXT中以B為頭的子串與S進行再一次比對。

　　　　而這樣的做法時間複雜度無疑是O(M*N); (M代表的是S的長度,N代表的是TEXT的長度);但是顯然B和A的比較是無意義的,因為我們知道一個以B開頭的子串是不可能與當前S串匹配的！

　　　　基於此我們推出升級版本的演算法:

　　　　　/**
	 * 升級版
	 * 猜想是否能有辦法加速匹配速度
	 * 如若我第i + j 與 j未匹配上 即:text.charAt(i + j) != s.charAt(j)
	 * 是不是可以直接從i = i + j + 1 , j = 0繼續匹配? 即 以頭為i + j + 1下標為頭的text子串與s串繼續匹配
	 * 不一定可以!,但有時候一定可以,那麼是在什麼時候？
	 * 如若我s.charAt(0)與下標在[1, j]內的s串的字元都不相等,那麼以[i + 1, i + j]為頭的Text子串都不可能匹配上s,
	 * 因為text[i + 1, i + j]與s[1, j]一一對應,所以text[i + 1, i + j]都不與s.charAt(0)匹配
	 * 因為連第一個元素都匹配不上,怎麼可能成功？
	 * 但如若[i + 1, i + j]內有等於第一個元素,那麼就不能直接跳到i = i + j + 1了,為什麼呢？
	 * 假若text.charAt(i + k) == s.charAt(0), k屬於[i + 1, i + j]
	 * 因為第一個字元能匹配就意味著在text.charAt(i + k + 1) != s.charAt(1)...之後都是有可能的
	 * 如若跳過可能直接跳過了正確結論
	 * 那麼基於以上結論我們可以做一個數組arr.
	 * 如若當前下標k和當前下標以前的節點沒有第二個s.charAt(0)
	 * 則當前節點值為 arr[k] = -1;
	 * 如若有且下標為p 則將第一個標誌出來
	 * arr[k] = p;
	 * 雖然這個升級版只對特殊s串有著顯著的加速作用,但它對於我們進一步推至KMP是很關鍵的一箇中間步驟
	 * @param text
	 * @param s
	 * @return
	 */
	public static int strStr1(String text, String s) {
		if (text == null || s == null || s.length() > text.length()) {
			return -1;
		}
		int[] help = getHelpArray(s);
		int i = 0, j = 0;
		while (i + j < text.length() && j < s.length()) {
			if (text.charAt(i + j) == s.charAt(j)) {
				j++;
			}else {
				if (help[j] == -1) {
					i = i + j + 1; j = 0;
				}else {
					i = i + help[j] + 1;  j = 1;
				}
			}
		}return j != s.length() ? -1 : i - j;
	}
	
	public static int[] getHelpArray (String s) {
		if (s == null || s.length() == 0) {
			return null;
		}
		int[] res = new int[s.length()];
		res[0] = -1; int first = -1;
		for (int i = 1; i < res.length; i++) {
			if (first == -1 && s.charAt(0) == s.charAt(i)) {
				first = i;
			}res[i] = first;
		}return res;
	}

　　　　基於以上結論 : 

　　　　條件 ：當前以及匹配了j個元素,在第j+1個元素時不匹配

　　　　1)S[0,j-1]與text[i,i+j-1]一一匹配,那麼我們可以通過這個容易忽略的性質加速演算法。

　　　　2)如若S[1,j]都不等於S.charAt(0)其實我們是有辦法利用1)性質來加速的

　　　　提出問題: 那麼我們能不能做到一個更嚴格的篩選呢？ 例如我們能不能把以i + k為頭的text子串如若存在text.charAt(i + k + e) != S.char.At(e);也給直接跳過了呢？ (k = 0是無意義的因為早就已經確認了,如若繼續加入k = 0,則重複了S[0,j-1]與text[i,i+j-1]一一匹配，故: K > 0)

　　　　在這裡e表示的是S串中第e個元素是否處在i+k為頭的text子串正確的位置i + k + e上,如若不然，則i + k直接可以"淘汰"。

　　　　顯然我們具備這個條件,只需要將text.charAt(i + k + e)找到之前與之對應的S串元素就可以在help陣列內就"淘汰"它！

　　　　但顯然我們有一個要求i + k + e < i + j 即 : k + e < j,因為只有在之前已經通過匹配的我們才知道他與S串的對應關係。 

　　　　對於 e < j - K ：

　　　　j代表的含義是當前已匹配的長度,K是以i + K為頭的text子串,也是以K為頭的S子串（因為1)中的一一匹配性質）而e是以K為頭的S子串所能匹配長度。

　　　　但是並非是e取最大的一個K子串就一定能確認他在j內是無法判斷是否可以淘汰的,只要k + e < j,有一個字元無法匹配,那麼我就一定能確認它要被淘汰,那麼我就不用考慮i + k，而是考慮其他的。

如若S.charAt(k + e) != S.charAt(e)在e的取值範圍e < j - K(此時K已選定)時都能成立,那麼我就無法再不再次匹配時將他淘汰。其實這時候的S[0,e]與S[k,k+e]一一對應的關係有專業的名稱，而我們推出的結論也就是著名的KMP演算法:

　　　　首先在這裡提出一個字首串和字尾串的概念 : 字首串簡單來說就是在這個字串下標包含[0,e]的一個子串,不過他得從0開始。與字首串類似 字尾串是由 [k,j - 1]的一個子串,看到這是不是很眼熟？因為這就是我們之前所推的 S[0,e]與S[k,k+e]一一對應的關係,且因為如若e < j - k就會被淘汰,故而變成了S[0,e]與S[k,j - 1]。

　　　　　　另一個概念 : 最大相等字首字尾長度。

　　　　　　例如 : ABAB 最大相等字首字尾長度是2,如若取3，則字首串為ABA字尾串為BAB，無法匹配。

　　　　　　AIJDWOA 最大相等字首字尾長度是1

　　　　　　AAAA 最大相等字首字尾長度是3，為什麼不是4？ 因為要求K != 0,也就是說字首串和字尾串不能是它本身,這點很重要。如若取他本身則在KMP中會發生無法避免的死迴圈。

　　　　　　為什麼要提出最大相等字首字尾長度這個概念？

　　　　　　因為S[0,e]與S[k,j - 1]一一匹配,如若有一個滿足e最大 可以退出 k是最小符合條件的,那麼就不會漏出未淘汰部分。而且最大相等字首字尾長度其實就是e+1（e是下標從0開始數）.

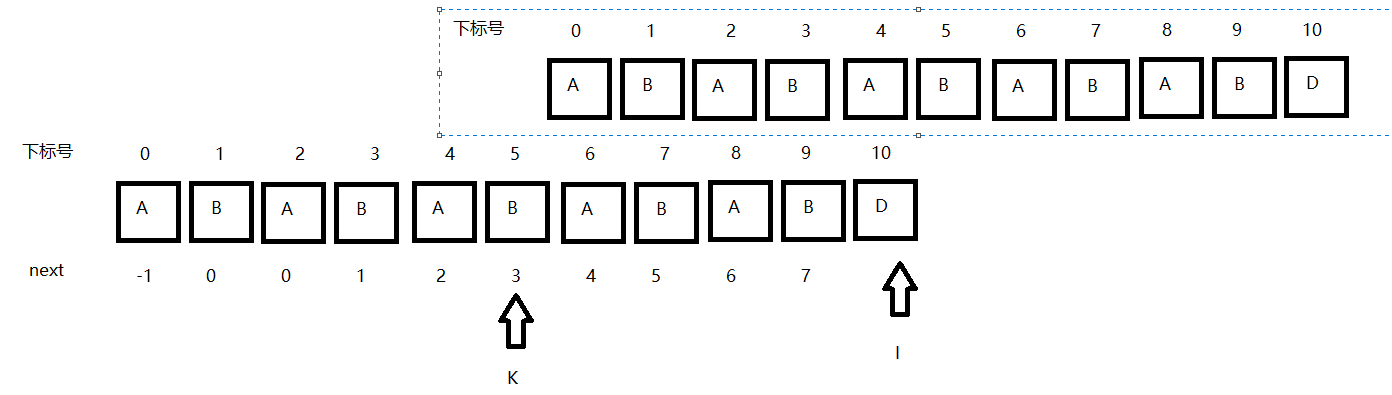
　　　　　　舉例說明 : 這裡的i與上兩個程式的i不同，不再是代表以i為頭的子串的那個i，而是單純的讓i與j進行比較。

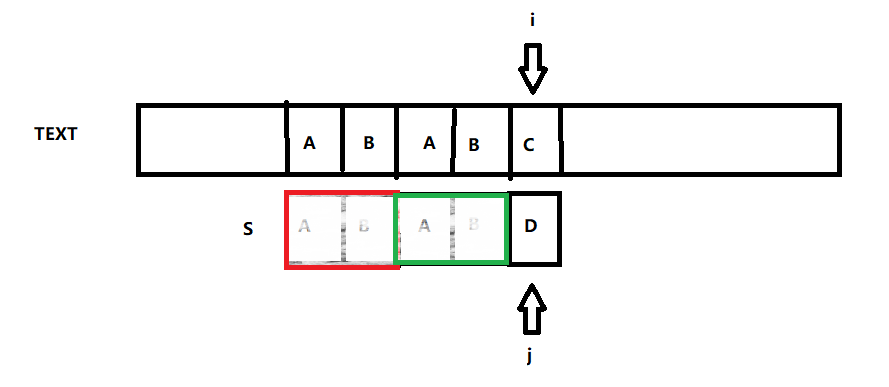
　　在上圖S串中最大相等字首字尾長度為2（U）,那麼我們如若將j移動到2(U)(這裡的2即是最大相等字首字尾長度),而i不變就繼續進行匹配,而且如若你舉更多例子也仍然可以進行這種操作。這樣的話我們就可以無論什麼情況,都能達到i不後退！這就意味著我們的演算法可能可以優化到了O(N)！

　　為什麼是 j = U? 其實這就是說我們前面S.charAt[0,e]與S.charAt[K,K+e]與text.charAt[(i-j) + K,(i-j) + K+e]都一一對應了,i-j代表的是當前正以i-j開頭的子串進行匹配。

　　既然我們已經知道了[0,e]都滿足條件了,那麼直接移動j至e+1比對即可！

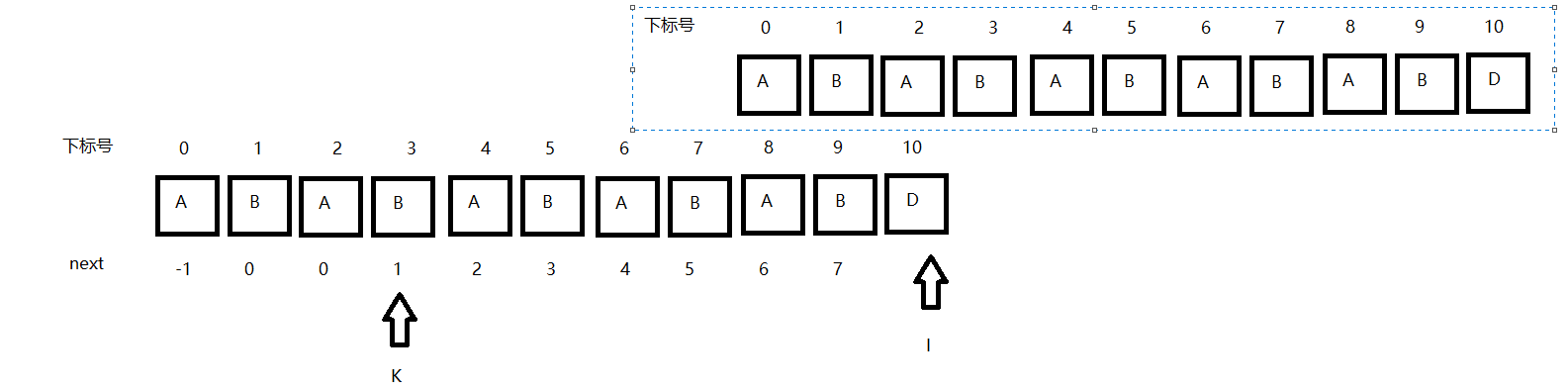
　　但如若再次沒比對成功呢？

　　如上圖,如若j已經指向A，依然A!=C又該如何辦呢？

　　這個問題看似複雜，但其實我們已經解決過了,這就是我們j指向D時候的問題嘛,前面都匹配,在j位置上時與i不匹配,那麼上一次怎麼解決的這次就怎麼解決,唯一的不同就是U是這次對應的U，如若我們早已經把U放入help陣列內，那麼上一次是j = help[U];這一次仍然是。

　　那麼如何求得我每次要的最大相等字首字尾長度？

　　將這部分問題獨立起來(求最大相等字首字尾長度問題)並且簡要概述:

　　　　有一字串S，要求求出S每個下標index(依次為1,2,3,4...)前面index個字元組成的子串的最大相等字首字尾長度並儲存在陣列內返回

　　　　public int[] getNextArray (char[] ch){ //這裡使用char[]會比較方便

　　　　}

如若採取常規做法 : 這是很明顯的O(M*M)

　　常規演算法根本在於 從 i-1 開始猜測U並驗證,直到找到真正的U

　　　　　/**
	 * 判斷每個字元的字首最大對稱 並且將資料組成陣列返回
	 * @param str
	 * @return
	 */
	public static int[] makeNext(char[] ch) {
		if (ch == null) {
			return null;
		}
		int N = ch.length;
		if (N == 1) {
			return new int[]{-1};
		}else if (N == 2) {
			return new int[]{-1, 0};
		}
		int[] next = new int[ch.length];
		//next[0]填入-1 而不是0 是為了標誌這是0號元素 避免使用的時候發生死迴圈
		//當然 你也可以直接在next[0]填入0 然後用下標識別
		next[0] = -1; next[1] = 0;
		for (int i = 2; i < N; i++) {
			int res = i - 1, j = 0;
			while (j < res) {
				if (ch[i - res + j] == ch[j]) {
					j++;
				}else {
					res--; j = 0;
				}
			}next[i] = res;
		}
		return next;
	}

　　但是很幸運,我們有更好的方法來實現這個功能！

　　先貼程式碼後講解:

　　　　public static int[] getNextArray (char[] ch) {
		if (ch == null) {
			return null;
		}
		int N = ch.length;
		if (N == 1) {
			return new int[]{-1};
		}else if (N == 2) {
			return new int[]{-1, 0};
		}
		int[] next = new int[ch.length];
		next[0] = -1; next[1] = 0;
		//這裡的k在i++後其實就是next[i-1]但是有時候k與i-1沒匹配上,意義就不再是這樣了。
		//在下面註釋部分其實就是{}內語句的另一種形式 他們所起的作用是相等的
		int k = 0, i = 2;
		while (i < N) {
			if (ch[k] == ch[i - 1]) {
				next[i++] = ++k;
//				k++;
//				next[i] = k;
//				i++;
			}else if (k > 0) {
				k = next[k];
			}else {
				next[i++] = 0;
//				next[i] = 0;
//				i++;
			}
		}return next;
	}

　　採用這種做法的想法應該是: 我能不能找到某種next[i-1]與next[i]的聯絡來加速演算法？

　　首先我們已知的是

　　S.charAt[0,next[i-1]-1]與S.charAt[(i-2)-next[i-1]-1,i-2]一一匹配

　　那麼如若S.charAt(next[i-1]) == S.charAt(i-1)即可知道next[i] = next[i-1]+1;

　　　　為什麼不能是next[i-1]+p,p屬於[2,正無窮]

　　　　　　因為如若取得next[i-1] + p,那麼就代表有

　　　　　　S.charAt[0,next[i-1] + p - 1]與S.charAt[(i-2)-next[i-1]-p+1,i-1]一一匹配

　　　　　　這裡包含了一個資訊即: [0, next[i-1] + p - 2] 與 [(i-2)-next[i-1]-p+1,i-2]是匹配的,而且next[i-1] + p - 2 > next[i-1]-1

　　　　那麼next[i-1]就不是最大相等字首字尾長度了。

　　那麼如若S.charAt(next[i-1]) != S.charAt(i-1) 就要往回跳了

　　但是這個問題好像怎麼這麼熟悉？？？

　　字串匹配演算法？

　　對的,他還是字串匹配演算法,而且是已知help[0,i-1]的字串匹配演算法。當然,初學時候你或許不能很明白地看出來。

　　在這個圖裡我把下標i-1弄成了I,你就理解為 I = i - 1 吧..（非常抱歉,大家知道就好了..）。

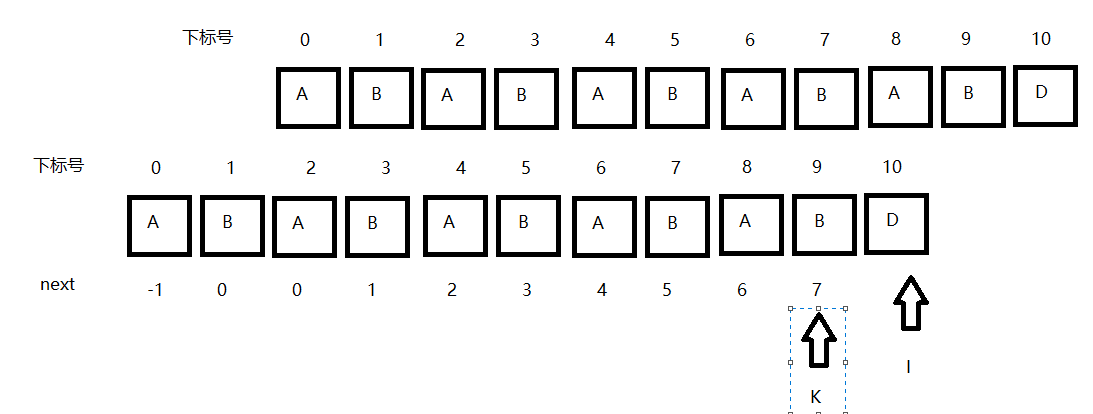
　　在這裡下面的代表的是S串,下面的代表著next串，並且兩個串都具有help[0,i-1]根據之前我們得出的結論,即

　　如若  ch[k] == ch[i-1],這裡的i-1就是之前的討論KMP時的i，為待匹配元素下標,這裡的k就是之前的j為匹配元素下標。

　　那麼i++, j++; 但在這裡就意味著next[i] = next[i-1] + i;也就是當前最大相等字首字尾長度是前一個最大相等字首字尾長度+1；

　　如若ch[k] != ch[i-1],那麼 k = next[k]；也就是 j = U,在這裡j就是k, U就存在netx[j]裡面,也就是說 k = next[k]。

　　getNextArray();的另一種解釋:

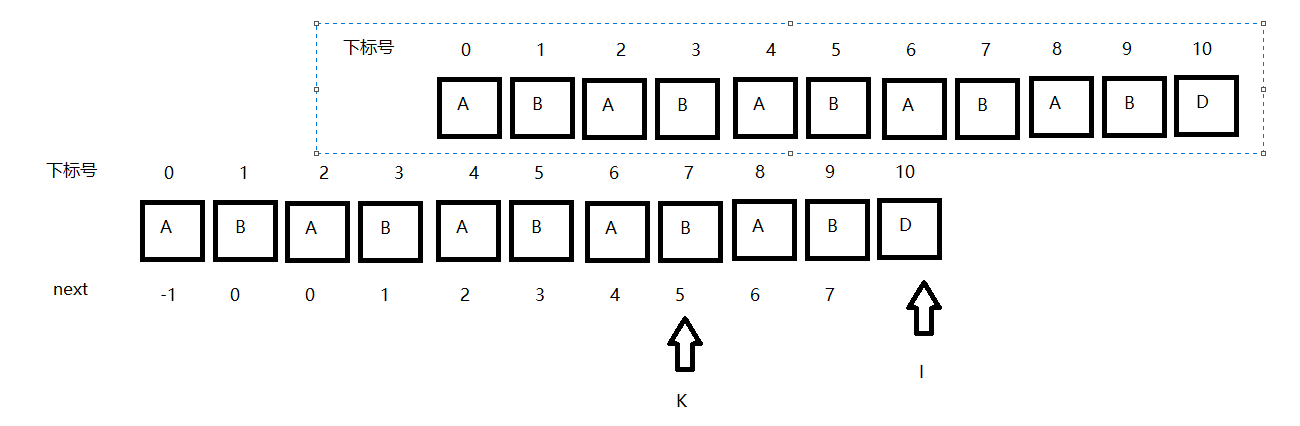
　　在圖片示例中我們可以清楚的看到下標k的移動,k = next[k]就是說下一次與i進行比對的就是next[k]內元素,next[k]內元素即是以k為下標的前k個子串的最大相等字首字尾長度.

　　那麼為什麼要這麼跳？

　　　　這意思是一個下標對應的結果只能是[0,next[k]] U [k+1,k+1],這裡k的初始值是next[i-1]。

　　　  這是一個有點遞迴感覺的區間,但顯然[0,next[k]]中間並非是連續的整數,是否可取取決於資料情況。

　　　　證明 : 一個下標對應的結果只能是[0,next[k]] U [k+1,k+1]

　　　　為什麼不能取到一個結果大於k+1? 

　　　　　　在第一種解釋就解釋了！

　　　　為什麼不能取到(next[k],k+1)的值？

　　　　　　如若取得這部分值,那麼就代表e + 1變短了,或者取到了淘汰的值,那麼就可能遺漏掉正確結論（講最大相等字首字尾長度之前講過）。而next[k]是當前最"巧"值,比k+1大就就證明next[k]不是最大相等字首字尾長度,取(next[k],k+1)就跳過頭了,可能跳過正確結論,例如next[k]開頭的子串就可能是結果。如若取< next[k]那就取到了已淘汰的值,浪費了之前辛辛苦苦求出來的next資料！

　　KMP演算法:

/**
	 * KMP演算法
	 * @param 
	 * @param haystack
	 * @return
	 */
	public static int strStr2(String haystack, String needle) {
		if (needle.length() > haystack.length()) {
			return -1;
		} else if (needle.length() == 0) {
			return 0;
		}
		char[] ch1 = needle.toCharArray();
		char[] ch2 = haystack.toCharArray();
		// 獲取next陣列
		int[] next = getNextArray(ch1);
		int i = 0, j = 0;
		// 比對
		while (j < ch2.length && i < ch1.length) {
			if (ch1[i] == ch2[j]) {
				i++;
				j++;
			} else if (next[i] != -1) {
				i = next[i];
			} else {
				j++;
			}
		}
		return i == ch1.length ? j - i : -1;
	}

　　其實KMP與getNextArray();是同一原理。在懂得了這一原理後,理解程式碼應該是比較容易的，所以我就不一一贅述了。

　　結尾是一些想法:

　　　　為什麼KMP很難掌握而且又很容易忘記？因為這個演算法確實是具有高難度的,思路十分精妙,尤其是getNextArray中再次將其提取為字串匹配問題,且利用已有前i-1個元素的next求出第i個元素的next。是在令人驚歎。同樣,這一部分程式碼也最為關鍵。不要以為它是一個輔助函式，其實它才是KMP的關鍵所在。所以一定要重視,多分析幾次！

　　以下是簡單證明,寫的不算嚴格,但自己看了一遍覺得還是表達出了意思,這個證明有興趣可以自己寫個嚴格的,並且面試會考這個:

　 為什麼是O(N)?

　　　　1)如若TEXT比S短 : 那麼我們不可能再TEXT中找到一個子串等於S，return -1；

　　　　2)如若TEXT.length() >= S.length() : 

　　　　有可能會有人覺得如果我S串極其特殊,且i指向的元素每次都不與j指向元素匹配呢？

　　　　例如 : 

　　　　TEXT : ABABABABC...

　　　　　　　 012345678

　　　　S : ABABABABD 

　　　　　　012345678

　　　　初始i = 8, j = 8; 第一次跳躍到j = 6,i不變,不匹配；第二次j = 4,不匹配；j = 2,不匹配那麼這個長度就與M相關了,並且我僅僅需要隔著一段再出現這種資料就行了　　　　　　　　                  若 TEXT : ABABABABCABABABABCABABABABCABABABABCABABABABCABABABABCABABABABCABABABABCABABABABC...

　　　　那麼我不就很有可能就跌到了O(K*M*N)?

　　　　其實不會

　　　　1) 初始 J = 0 : 

　　　　　　i) i,j不匹配.i++;

　　　　　　ii) i,j匹配,i++;j++;

　　　　2)J = K : 

　　　　　　i)i,j不匹配,j往回跳K/X次數 （X>=1）

　　　　　　ii)i,j匹配, i++;j++;

　　　　在2)i)這裡i,j不匹配往回跳K/X次數 (X>=1),但這裡有一個很重要的前提即:J = K。 那麼證明前K次是匹配的,這K次是N的一部分,那麼對於這一部分來說就是(K-1) + K/X < 2K，就算全域性都是之前舉例的TEXT,那麼 也只能是 N/K * ( K-1 + K/X ) < 2 * N。在這裡K代表的是小於N,大於等於0的任意值,即使會有K1,K2,K3...每次K不一樣,但K1 + K2 + K3...+ Kn  = N一樣是成立的,那麼結果也會小於2*K1 + 2*K2 + 2*K3 +...+ 2*Kn  = 2 * N;

　　　　所以無論多麼極端的資料,也最大為2 * N;