poj2676(dfs+回溯)
| Sudoku
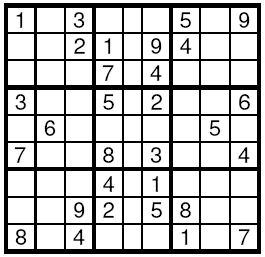
Description Sudoku is a very simple task. A square table with 9 rows and 9 columns is divided to 9 smaller squares 3x3 as shown on the Figure. In some of the cells are written decimal digits from 1 to 9. The other cells are empty. The goal is to fill the empty cells with decimal digits from 1 to 9, one digit per cell, in such way that in each row, in each column and in each marked 3x3 subsquare, all the digits from 1 to 9 to appear. Write a program to solve a given Sudoku-task. Input The input data will start with the number of the test cases. For each test case, 9 lines follow, corresponding to the rows of the table. On each line a string of exactly 9 decimal digits is given, corresponding to the cells in this line. If a cell is empty it is represented by 0. Output For each test case your program should print the solution in the same format as the input data. The empty cells have to be filled according to the rules. If solutions is not unique, then the program may print any one of them. Sample Input Sample Output Source |
||||||||||
填完數獨,不能有同行,不能有同列,不能有同一方格
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define maxn 50 using namespace std; int row[maxn][maxn]; int col[maxn][maxn]; int gird[maxn][maxn]; int mp[maxn][maxn]; bool dfs(int r,int c) { if(r==9) return true; bool flag=false; if(mp[r][c]) {if(c==8) flag=dfs(r+1,0); else flag=dfs(r,c+1); return flag; } int k=(r/3)*3+c/3; for(int i=1;i<=9;i++) { if(!row[r][i]&&!col[c][i]&&!gird[k][i]) { row[r][i]=col[c][i]=gird[k][i]=true; mp[r][c]=i; if(c==8) flag=dfs(r+1,0); else flag=dfs(r,c+1); if(flag) return true; mp[r][c]=0; row[r][i]=col[c][i]=gird[k][i]=false; } } return false; } int main() { int t; scanf("%d",&t); while(t--) { memset(row,0,sizeof(row)); memset(col,0,sizeof(col)); memset(gird,0,sizeof(gird)); for(int i=0;i<9;i++) for(int j=0;j<9;j++) {char x; scanf(" %c",&x); mp[i][j]=x-'0'; if(mp[i][j]) { row[i][mp[i][j]]=true; col[j][mp[i][j]]=true; int k=(i/3)*3+j/3; gird[k][mp[i][j]]=true; } } dfs(0,0); for(int i=0;i<9;i++) {for(int j=0;j<9;j++) printf("%d",mp[i][j]); printf("\n"); } } return 0; }