【機器學習】基於梯度下降法的自線性迴歸模型
阿新 • • 發佈:2018-11-26
回顧
線性迴歸的損失函式為:
梯度下降法求解結果為:
上式為對於一個樣本的對 梯度,在求梯度時,需要遍歷每個
for j in range(樣本特徵數)
的更新公式為:
以上
基於梯度下降法的自線性模型
- 構建模型訓練函式
fit()
fit(X, Y, alphas, threshold=1e-6, maxIter=200, addConstantItem=True)
引數:
- X:訓練資料特徵,X必須是List集合
- Y:訓練資料標籤,Y也必須是List集合
- alphas:學習率
- threshold:損失函式值小於此值停止迭代
- maxIter:迭代次數
- addConstantItem:是否有常數項
再呼叫模型訓練函式後,我們需要對傳入的訓練資料進行校驗,滿足條件才能進行梯度計算以及引數的更新
- 1.校驗資料
def validate(X, Y):
if len(X) != len(Y): # 特徵資料與標籤資料個數不一樣
raise Exception("引數異常")
else:
m = len(X[0]) # 第一個樣本的特徵數目
for l in X: # 遍歷所有樣本
if len(l) != m: # 只要有一個樣本的特徵數目與第一個不一樣
raise Exception("引數異常")
if len(Y[0]) != 1: # 不是單標籤
raise Exception("引數異常")
- 2.計算 差異值
# x表示一個樣本,y表示對應的標籤,a表示theta值
def calcDiffe(x, y, a):
# 計算y - ax的值
lx = len(x) # 特徵數目
la = len(a) # theta個數
if lx == la: # 相等的話就不包含常數項
result = 0
for i in range(lx):
result += x[i] * a[i] # 相乘求和
return y - result
elif lx + 1 == la: # 特徵個數比theta多一個,表示有一個是常數項
result = 0
for i in range(lx):
result += x[i] * a[i]
result += 1 * a[lx] # 加上常數項
return y - result
else : # 否則引數異常
raise Exception("引數異常")
- 3.模型訓練
def fit(X, Y, alphas, threshold=1e-6, maxIter=200, addConstantItem=True):
"""
X:訓練資料特徵,X必須是List集合
Y:訓練資料標籤,Y也必須是List集合
alphas:學習率可選範圍
threshold:損失函式值小於此值停止迭代
maxIter:迭代次數
addConstantItem:是否有常數項
"""
# 資料校驗
validate(X, Y)
# 開始模型構建
l = len(alphas) # 學習率的個數
m = len(Y) # 標籤個數
n = len(X[0]) + 1 if addConstantItem else len(X[0]) # 樣本特徵的個數,如果有常數項就+1
# 模型的格式:控制最優模型
B = [True for i in range(l)]
# 差異性(損失值)
J = [np.nan for i in range(l)] # loss函式的值
# 1. 隨機初始化theta值(全部為0), a的最後一列為常數項
a = [[0 for j in range(n)] for i in range(l)] # theta,是模型的係數,有len(alpha)組,分別記錄每個學習率的模型係數
# 2. 開始計算
for times in range(maxIter): # 迭代次數
for i in range(l): # 選擇學習率
if not B[i]:
# 如果當前alpha的值已經計算到最優解了,那麼不進行繼續計算
continue
# 梯度下降計算(計算所有資料)
ta = a[i] # 第i組theta值,與alpha對應
for j in range(n): # 遍歷樣本特徵
alpha = alphas[i] # 選擇學習率
ts = 0
for k in range(m): # 遍歷所有樣本
if j == n - 1 and addConstantItem: # 最後一個是常數項將公式中的x_j設為1
ts += alpha*calcDiffe(X[k], Y[k][0], a[i]) * 1
else: # 其他的theta更新公式後半部分按公式計算
ts += alpha*calcDiffe(X[k], Y[k][0], a[i]) * X[k][j]
t = ta[j] + ts # 更新theta
ta[j] = t # 記錄新的theta
# 計算完一個alpha值的theta的損失函式
flag = True
js = 0
for k in range(m):
js += math.pow(calcDiffe(X[k], Y[k][0], a[i]),2) # 損失函式
if js > J[i]:
flag = False
break;
if flag:
J[i] = js
for j in range(n):
a[i][j] = ta[j] # 更新theta
else:
# 標記當前alpha的值不需要再計算了
B[i] = False
# 計算完一個迭代,當目標函式/損失函式值有一個小於threshold的結束迴圈
r = [0 for j in J if j <= threshold]
if len(r) > 0:
break
# 如果全部alphas的值都結算到最後解了,那麼不進行繼續計算
r = [0 for b in B if not b]
if len(r) > 0:
break
# 3. 獲取最優的alphas的值以及對應的theta值
min_a = a[0]
min_j = J[0]
min_alpha = alphas[0]
for i in range(l):
if J[i] < min_j:
min_j = J[i]
min_a = a[i]
min_alpha = alphas[i]
print("最優的alpha值為:",min_alpha)
# 4. 返回最終的theta值
return min_a
- 預測結果與模型評估
# 預測結果
def predict(X,a):
Y = []
n = len(a) - 1
for x in X:
result = 0
for i in range(n):
result += x[i] * a[i]
result += a[n]
Y.append(result)
return Y
# 計算實際值和預測值之間的相關性
def calcRScore(y,py):
if len(y) != len(py):
raise Exception("引數異常")
avgy = np.average(y)
m = len(y)
rss = 0.0
tss = 0
for i in range(m):
rss += math.pow(y[i] - py[i], 2)
tss += math.pow(y[i] - avgy, 2)
r = 1.0 - 1.0 * rss / tss
return r
模型比較
至此,基於梯度下降法的自線性迴歸模型就構建好了,下面我們可以利用自模型進行訓練,並與sklearn庫中的線性迴歸模型進行對比,對比結果如下:
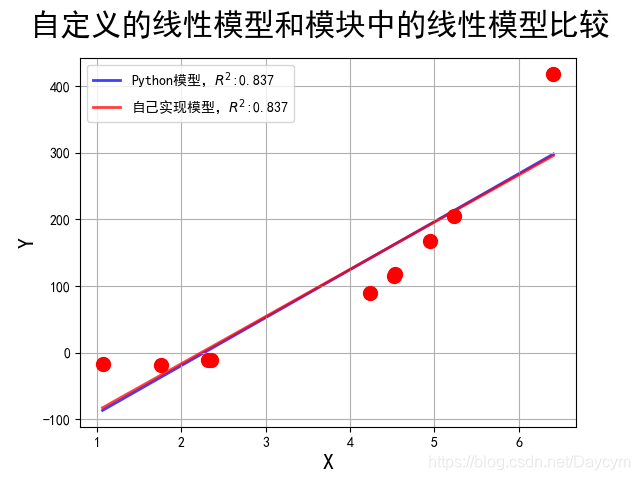
上圖我們可以發現,自己實現的模型與python自帶的模型的結果基本一致
原始碼
Github下的08_基於梯度下降法的線性迴歸.py
