8.霍夫變換:線條——介紹、引數模型、直線擬合_1
目錄
介紹
引數模型
直線擬合
介紹
到目前為止,我們一直在做影象處理,你把一個影象 和 應用一些函式相加得到一個新的影象我標記為
。
這很好,整個課程,實際上是整個職業生涯,數以萬計的PHD寫在影象處理上。
但這不是我們來這裡的原因。
我們來談談真正的計算機視覺。
在真實的視野中,你仍然可以拍攝一張照片,但你得到的是好東西。
整個想法是我們把影象放進去,然後把東西拿出來。
那麼有哪些例子呢?
也許只是一條線。
左邊有一張圖片中間有一些關於它的邊緣描述,你可以看到這張圖片中有很多線條。
或者你想找到圓:
實際上這有點難看,但是有個保齡球。
找到保齡球的方法是找到影象中的所有圓圈。
嗯,你猜怎麼著?
只有一個圓,那就是保齡球。
或者,這裡還有一些硬幣:
只要找到硬幣就行了。
事實上,我要告訴你們這張特別的圖片是很多年前,由我的一個朋友拼湊起來的。
他現在是一個非常著名的研究員,在做一些我不能說的事情。
但這是為了展示如何對圓進行霍夫變換。
你甚至可以找到類似的東西,幫我找到這輛車:
你們可以看到,在左邊這裡有一些我們可以定位汽車的例子。
但實際上,汽車就在中間。
實際上,這是一個任意形狀的概念,我們會講到如何求任意形狀。
現在我們即將討論廣義霍夫變換。
引數模型
今天我們將關注於尋找引數模型。
引數模型的意思是它是一個類,它是一個模型,它代表了一組例項,每個例項都可以用引數的特定設定來表示。
例如,直線是引數模型。圓是一個引數模型。
而且,就像我說的,我們甚至可以談論一個引數化模板,你有一個模板,你可以根據一些引數的值改變它的形狀。
所以,當你試著去擬合一個引數模型,或者換句話說,你試著在你的影象中找到一個引數模型。
它們本質上是一個杯子,有一些東西你必須記住。
首先,你要用什麼引數模型?
也就是說,如何表示,如何從引數到所表示的東西。
事實上,今天,我們將向你們展示即使對於像直線這樣簡單的東西,引數化是如何起作用的。
關於這個模型的另一件事,這實際上對我們有利,就是影象中的一點或者邊緣或模板屬於模型的概念,
不僅僅是通過檢視邊緣來確定,你需要觀察很多不同的邊或者整個模型。
擴充套件支援的概念是我們要利用的。
最後,當你去尋找引數模型時,你可以說,如果電腦是無限快的,每次我們使用一個電腦,它們就會覺得自己變得無限快。
我只需要在所有可能的地方檢查每一條線。
事實上,即使是非常非常非常快的電腦,可能的模型的數量非常非常非常大,結果是,你真的,真的,真的,我迷路了。
事實證明,你是一臺非常快的計算機,但是,你仍然需要擔心計算的組合問題。
直線擬合
這裡有一個簡單的例子。
你可能會想,我為什麼要找直線?
正如左邊的例子,你可能想知道晶片的位置是否正確,這樣你就能看到晶片上的線條。
或者這是得克薩斯大學的塔你發現的邊緣,你可能只是想看到你是否可能在州議會和你想確保塔德克薩斯大學不是向左傾斜。
這對你們有些人來說是個笑話。但現在我們假設,找到直線是我們想做的。
你可能會想,等一下,我們花了很長時間學習如何找到邊。
我們沒有完成嗎?我們不能找到邊嗎?
肯定可以找到!
我們來討論一下尋線的困難:
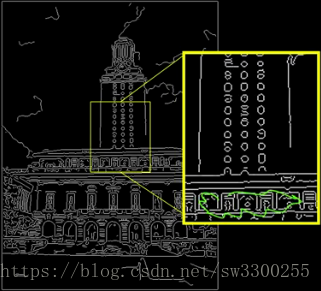
這是同樣的德克薩斯大學塔,還是由Christian Gromen贊助的,我們運行了一個邊緣檢測。
我在這裡做的是:我放大出了一部分出來,以便我們可以討論一些現象。
第一個問題是:這裡有很多與直線無關的點。
所以下面這些小的邊點,這些與直線無關,所以我們必須能夠高效快速地處理它們:
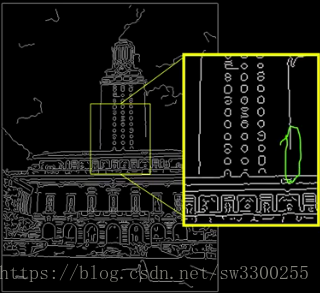
第二個問題:實際上只有部分線路被檢測到。
舉個例子,你可以看到這條線有一個很大的缺口:
儘管我們真正想做的是:找到整條直線。
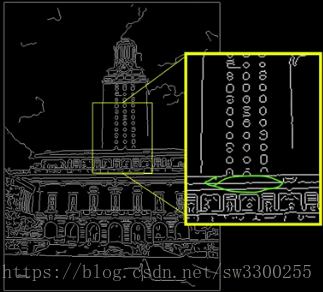
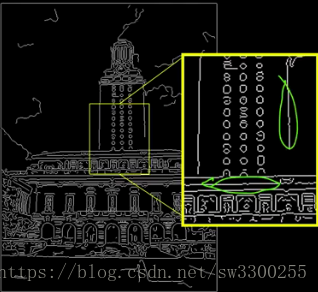
第三問題:噪音和不整齊實際上是可以幫助我們找到邊緣的地方。
在這裡,你會注意到,在這條線上,所有這些畫素並沒有完全在直線上:
你可以看到畫素也在這裡跳躍:
因此,我們必須能夠從這些噪聲測量到邊緣的位置,以便找到實際的線。
小測驗:
讓我們試著建立一些關於如何從邊到線的直覺。
記住,邊緣影象只是畫素的集合,像這樣的畫素,在那裡可以找到可能的線條。
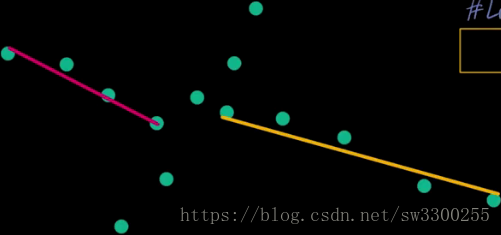
在這幅圖中你能識別多少行?
答案:你可以用不同的方式來識別線條。
例如,這可能是一條短的線段:
右手邊的一條長線段:
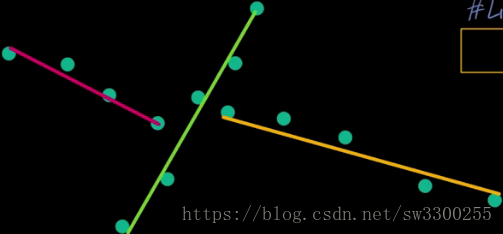
和一條對角線相交:
這是一組一致的線段,幾乎佔據了所有的邊緣點。
但還有其他的可能性。
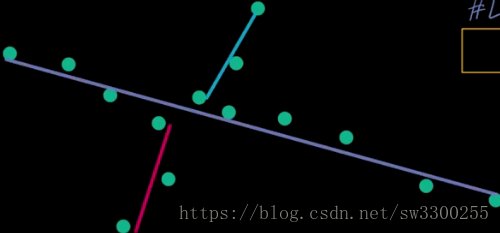
例如,這條長線段穿過,兩邊各有兩個短線段。
這個問題沒有唯一正確的答案。
希望這將使您瞭解如何在影象中查詢線段並不是一項簡單的任務。
——學會編寫自己的程式碼,才能練出真功夫。