圓方樹學習筆記
一直對聯通分量不怎麼了解
先開坑吧
$ tarjan$求割點
首先有一個性質:無向圖的$ dfs$樹沒有橫插邊
搜尋的時候判斷每個孩子能否回到自己上方
若不可行則自己為割點
注意特判根節點:只要自己的不聯通子樹數量$ \geq 2$則一定是割點
$ tarjan$求點雙連通分量
考慮$ tarjan$的時候
如果通過這個點的某子樹推出自己是割點
那麼從棧頂一直彈到把這個孩子彈出去再加上自己這個點一定構成點雙連通分量
放張圖吧
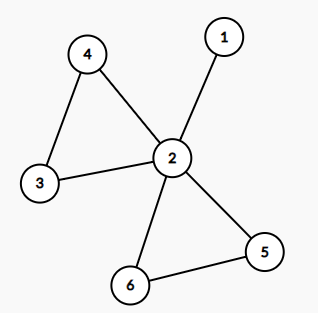
假設這張圖的$ dfs$序是$1 2 3 4 5 6$
維護搜尋棧:
$1 $
$1 、2$
$1 、2 、3$
$1 、2 、3 、4$
發現點雙:$2 、3 、4$ 彈出$ 3 、4$
$1 、2、 5$
$1 、2、 5 、6$
發現點雙:$2 、5 、6 $彈出$ 5、 6$
這樣就找出了所有點雙連通分量
構建圓方樹
如果我們對於每一個點雙連通分量以及大小為$ 2$的連通分量都新建一個點稱為方點
把原圖中的點稱為圓點
先刪除原圖上所有邊
對於每一個連通分量,我們把所有圓點往這個方點上連邊
這樣生成的樹稱為圓方樹
如上圖的圓方樹為:
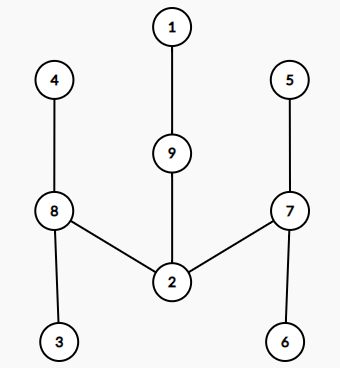
(請自行把點$ 7、8、9$腦補成方點)
圓方樹的性質:
1.不存在圓點-圓點邊以及方點-方點邊
2.圓方樹一定是一棵樹
3.如果原圖連通,構建出的圓方樹也一定連通
應用:
$ 1.$求仙人掌任意兩點間最短路:BZOJ 2125
直接構建圓方樹,圓點到方點的距離為這個圓點到這個方點父親的圓點在原圖上的最短距離
每次詢問求出$ LCA$,若$ LCA$是圓點則直接求路徑權值和
若$ LCA$是方點則跳到$ LCA$下面的圓點,然後求一下環上最短路即可
$ 2.$求從$ x$走到$ y$的路徑上可能經過的最小點權,帶修改 UOJ #30
如果兩個點經過了某個連通分量,一定可以走到這個連通分量的最小值
直接構建圓方樹,圓點存點權,方點用$ multiset$存連通分量的點權集合
通過一些巧妙的操作來減小修改的複雜度
$ 3.$求數對$(x,y,z)$的數量使得滿足存在一條$x$到$z$的路徑上經過$y$,要求$x,y,z$兩兩不同 APIO2018 鐵人兩項
直接構建圓方樹,令圓點權值為$ -1$,方點權值為$ size(點雙大小)$,然後直接在樹上做就好了
