仙人掌&圓方樹學習筆記+簡單應用

仙人掌&圓方樹學習筆記

前言

一直覺得仙人掌和圓方樹是非常高深的演算法。直到連續隨機跳題跳到兩道。我受不了啦！！！於是點進了一個連結。（傳銷現場有木有啊！）

推薦連結：戳這裡

然後發現並沒有想象中那麼難。而且，，，很好玩。日常賽前學演算法（大霧退役之前還是多多益善一波吧，錯過了可能就遇不上了！

定義:仙人掌

任意一條邊至多在一個環裡的無向聯通圖在這裡插入圖片描述

定義:仙人掌的圓方樹

仙人掌 $G = (V, E)$ 的圓方樹 $T = (V_T , E_T)$ 為滿足以下條件的無向圖: $V_ T = R_ T ∪ S_ T , R_ T = V, R_ T ∩ S_ T = ∅$

V_{T} = R_{T} \cup S_{T}, R_{T} = V, R_{T} \cap S_{T} = \emptyset

,我們稱

R_ T

集合為圓點、

S_ T

集合為方點

\forall e \in E

,若

e

不在任何簡單環中,則

e ∈ E_T

對於每個仙人掌中的簡單環

R

,存在方點

p_ R ∈ S_ T

,並且

\forall p \in R

滿足

(p _R , p) \in E_ T

,即對每個環建方點連所有點

嚴格的定義總是格外地難懂啊。簡單地說，把除了環上的所有邊保留。對於每個環，新建一個方點，把所有環上的點與這個方點連邊，刪除原有的環上的邊。

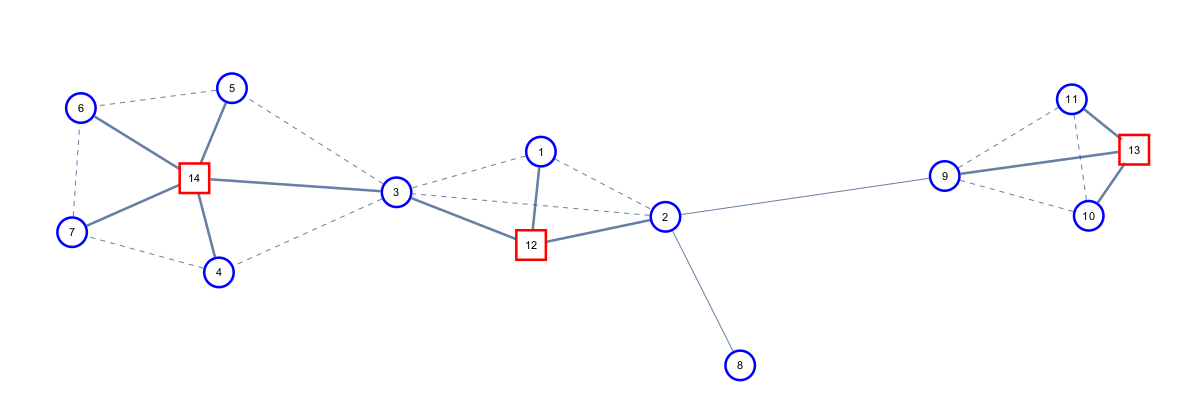
如何證明圓方樹是一棵樹？首先顯然，它仍然聯通。其次，對於每個環，新建的邊數等於刪除的邊數，點數多了一個。所以最後一定是一棵樹。

圓方樹的構造與性質

構造就是 $Tarjan$ 縮環啊。性質：

方點不會和方點連邊。（不然就有一條邊在兩個環裡了）
圓方數是一顆無根樹，無論以仙人掌的哪個根構建出來的圓方樹都是一樣地，進一步地，仙人掌的圓方樹和仙人掌是一一對應的。
定義以 $r$ 為根的仙人掌的 $p$ 子仙人掌為除去 $p$ 到 $r$ 的所有簡單路徑後， $p$ 所在聯通塊，則 $p$ 子仙人掌對應圓方樹就是 $r$ 的圓方樹上以 $p$ 為根的子樹。最後一條性質看上去很拗口。實際上，它想表達的意思是，仙人掌並不改變原圖任意兩點之間的連通性。這裡的連通性包括路徑資訊，連邊情況

等。

簡單圓方樹問題

題目大意：給定一個仙人掌，求最大獨立集。這道題其實並不需要真正建立出圓方樹。只需要在 $Tarjan$ 的時候把環的情況處理一下。具體地，對於樹邊，照常轉移。直接跳過環。然後在環上合併子樹的資訊。唯一不同的是如果當前子仙人掌的根要選，那麼環上和根相鄰的兩個節點都不能選（處理方法和基環樹類似）。

#include<bits/stdc++.h>
const int M = 130000, N = 55000;
int ri() {
    char c = getchar(); int x = 0, f = 1; for(;c < '0' || c > '9'; c = getchar()) if(c == '-') f  = -1;
    for(;c >= '0' && c <= '9'; c = getchar()) x = (x << 1) + (x << 3) - '0' + c; return x * f;
}
int to[M], nx[M], pr[N], g[N], dfn[N], low[N], f[N][2], tp, tm;
void add(int u, int v) {to[++tp] = v; nx[tp] = pr[u]; pr[u] = tp;}
void adds(int u, int v) {add(u, v); add(v, u);}
void Tra(int x[2], int y[2]) {x[0] += std::max(y[0], y[1]); x[1] += y[0];}
void Mg(int x[2], int y[2]) {int t = x[0] + y[0]; x[0] = std::max(t, x[1] + y[1]); x[1] = t;}
void Rdp(int u, int v) {
    int x[2] = {0};
    for(int i = v; i != u; i = g[i]) Mg(x, f[i]);
    f[u][0] += x[0]; x[0] = 0; x[1] = -1e9;
    for(int i = v; i != u; i = g[i]) Mg(x, f[i]);
    f[u][1] += x[1];
}
void Tar(int u, int fa) {
    dfn[u] = low[u] = ++tm; g[u] = fa; f[u][1] = 1; f[u][0] = 0;
    for(int i = pr[u]; i; i = nx[i]) {
        if(!dfn[to[i]]) Tar(to[i], u), low[u] = std::min(low[u], low[to[i]]);
        else if(to[i] != fa) low[u] = std::min(low[u], dfn[to[i]]);
        if(low[to[i]] > dfn[u]) Tra(f[u], f[to[i]]); //樹邊 
    }
    for(int i = pr[u]; i; i = nx[i]) //環 
        if(g[to[i]] != u && dfn[u] < dfn[to[i]]) 
            Rdp(u, to[i]);
}
int main() {
    int n = ri(), m = ri();
    for(int i = 1;i <= m; ++i) adds(ri(), ri());
    Tar(1, 0); printf("%d\n", std::max(f[1][1], f[1][0]));
    return 0;
}

題目大意：求仙人掌上任意兩點最短路，沒有負邊權。這題必須建出圓方樹。考慮邊權。圓圓邊不變，圓方邊定義為這個節點到環頂的最短距離（兩個方向比一下）。這樣，如果穿過了某個環，考慮兩種情況。

從環上某個結點 $v$ 進入，從環頂 $p$ 出。會經過一條邊權為 $dist(v,p)$ 的圓方邊和一條邊權為0的圓方邊( $dist(p,p)=0$ )，正好是穿過環的最短路。
從環上某個結點 $v$ 進入，從環上某個節點 $u$ 出。這樣子的話。起點終點在圓方樹上的 $Lca$ 必定是當前這個環對應的方點。用樹剖/倍增求出 $u$ , $v$ ，判斷哪個方向更加優秀即可。（類似基環樹的處理方法）

其餘情況不變，直接跑 $Lca$ 即可。這道題就很好地體現了圓方樹與仙人掌的對應關係。同時也提醒了我們在圓方樹上處理問題要重點考慮圓方邊，讓其儘量反映出原圖的各種性質。

#include<bits/stdc++.h>
const int N = 2e4 + 10;
int ri() {
    char c = getchar(); int x = 0, f = 1; for(;c < '0' || c > '9'; c = getchar()) if(c == '-') f  = -1;
    for(;c >= '0' && c <= '9'; c = getchar()) x = (x << 1) + (x << 3) - '0' + c; return x * f;
}
int fa[N], de[N], tot, n; 
struct Edge {
    int to[N << 2], nx[N << 2], w[N << 2], pr[N], tp;
    void add(int u, int v, int W) {to[++tp] = v; nx[tp] = pr[u]; pr[u] = tp; w[tp] = W;}
    void adds(int u, int v, int w) {add(u, v, w); add(v, u, w);} 
};
struct Round_Square_Tree {
    Edge T; int sz[N], fa[N], ds[N], de[N], d[N], di[N], c[N];
    void dfs1(int u, int ff) {
        fa[u] = ff; de[u] = de[ff] + 1; sz[u] = 1;
        for(int i = T.pr[u], v; i; i = T.nx[i]) 
        if((v = T.to[i]) != ff){
            di[v] = di[u] + T.w[i]; dfs1(v, u);
            sz[u] += sz[v]; sz[ds[u]] < sz[v] ? ds[u] = v : 0;
        }
    }
    void dfs2(int u, int c) {
        d[u] = c; if(!ds[u]) return ; dfs2(ds[u], c);
        for(int i = T.pr[u]; i; i = T.nx[i]) 
            if(T.to[i] != ds[u] && T.to[i] != fa[u]) 
                dfs2(T.to[i], T.to[i]);
    }
    int Lca(int u, int v) {
        for(;d[u] != d[v]; u = fa[d[u]]) de[d[u]] < de[d[v]] ? u ^= v ^= u ^= v : 0;
        return de[u] < de[v] ? u : v;
    }
    int Jump(
              
           
              
              
            
            相關推薦
			   
            
            
            
 

    

    
    仙人掌&圓方樹學習筆記+簡單應用
      
							
							
							仙人掌&圓方樹學習筆記
前言
一直覺得仙人掌和圓方樹是非常高深的演算法。
直到連續隨機跳題跳到兩道。我受不了啦！！！
於是點進了一個連結。（傳銷現場有木有啊！）
推薦連結 ：戳這裡
然後發現並沒有想象中那麼難。
而且，，，
很好玩。
日常賽前學演算法（大 

  
 

    

    
    仙人掌圓方樹學習筆記
      以後會逐漸完善，現在會先存放一些程式碼 
廣義圓方樹對於每個仙人掌的環新建一個方點，原仙人掌上的點為圓點，向這個環上的所有圓點連邊，使得所有的邊連線的都是 $ 1 $ 個圓點和 $ 1 $ 個方點 
廣義圓方樹長這個樣子 
 
然後就可以用樹形 dp 的方法來解決很多仙人掌上的問題啦 
bzoj 4316（求 

  
 

    

    
    仙人掌&圓方樹學習筆記
      仙人掌&圓方樹學習筆記
1、仙人掌
圓方樹用來幹啥？
——處理仙人掌的問題。
仙人掌是啥？

(圖片來自於\(BZOJ1023\))
——也就是任意一條邊只會出現在一個環裡面。
當然，如果你的圖片想看起來舒服一點，也可以把圖片變成這樣子

(圖片來源於網路)
2、DFS樹
為啥要寫這個？--因為這個看 

  
 

    

    
    仙人掌&圓方樹學習筆記
      https   思維題   bzoj   不變   n)   條件   連通性   普通   一朵   仙人掌&圓方樹學習筆記
1、仙人掌
圓方樹用來幹啥？
——處理仙人掌的問題。
仙人掌是啥？

(圖片來自於\(BZOJ1023\))
——也就是任意一條邊只會出現在一個環裏面。
當然，如果你的圖片想 

  
 

    

    
    洛谷4630 BZOJ APIO2018 鐵人兩項 圓方樹 dp （圓方樹學習筆記）
       
 
  
  
 題目連結 題意：給你一個n個點m條邊的無向圖，求所有的能從s到c再到t的三元組個數，其中每個點在一條路徑上至多經過一次。n,m1e5量級。 
 題解： 首先介紹一下圓方樹。 
 還記得zyb大佬憑藉圓方樹在APIO拿AU並在SD二輪進隊，近年來圓方樹也成為了一個熱門演算法，於是還是很有必 

  
 

    

    
    圓方樹學習筆記
      一直對聯通分量不怎麼了解 
先開坑吧 
 
$ tarjan$求割點 
首先有一個性質：無向圖的$ dfs$樹沒有橫插邊 
搜尋的時候判斷每個孩子能否回到自己上方 
若不可行則自己為割點 
注意特判根節點：只要自己的不聯通子樹數量$ \geq 2$則一定是割點 
 
  
$ tarjan 

  
 

    

    
    CF487E Tourists + 圓方樹學習筆記（圓方樹+樹剖+線段樹+multiset)
      QWQ果然我已經什麼都學不會的人了。 
這個題目要求的是圖上所有路徑的點權和！QWQ（我只會樹上啊！） 
這個如果是好啊 
這時候就需要 
圓方樹！ 
首先在介紹圓方樹之前，我們先來一點簡單的前置知識 
首先，我們需要知道什麼是 
點雙聯通分量 
若一個無向圖中的去掉任意一個節點都不會改變此圖的連通性，即不存 

  
 

    

    
    圓方樹和廣義圓方樹學習小記
      
							
							
							圓方樹，解決毒瘤仙人掌問題的利器。

有了圓方樹，什麼樹上的演算法都可以套在仙人掌上了，比如說點分治、樹鏈剖分、虛樹等等。

OI資料結構無窮無盡，只有你不會的，沒有你想不到的。

資料參見WC2017講稿。



圓方樹：

圓方樹分為圓點和方點。

圓點就是 

  
 

    

    
    【模板】靜態仙人掌(圓方樹)
      仙人掌圖   getchar   size   str   ++i   fin   etc   pro   lock   
 傳送門 
Description 

給你一個有\(n\)個點和\(m\)條邊的仙人掌圖，和\(q\)組詢問
每次詢問兩個點\(u,v\)，求兩點之間的最短路。

Solution 
 

  
 

    

    
    [學習筆記]圓方樹
      由於   圓點   大堆   分類討論   ace   可能   detail   成了   基本   圓方樹：元芳你怎麽看
 
圓方樹推薦

 
 
圓方樹是什麽？
Tarjan家族中，最不好處理的是點雙
因為一個割點可能屬於很多的DCC。
為了把圖縮成一棵樹，我們不得不做出這樣的處理：
摘自：https: 

  
 

    

    
    【BZOJ2125】最短路（仙人掌，圓方樹）
      return   namespace   tdi   ring   fine   .com   HA   names   truct   【BZOJ2125】最短路（仙人掌，圓方樹）
題面
BZOJ
求仙人掌上兩點間的最短路
題解
終於要構建圓方樹啦
首先構建出圓方樹，因為是仙人掌，和一般圖可以稍微的不一樣
 

  
 

    

    
    仙人掌&圓方樹
      sdoi   uoj   problem   仙人掌圖   clas   ref   zoj   .org   http   仙人掌&圓方樹
Tags：圖論

占個坑？
咕咕咕

[x] [luogu4320]道路相遇 https://www.luogu.org/problemnew/show/P43 

  
 

    

    
    bzoj4564: [Haoi2016]地圖 仙人掌的圓方樹 莫隊 分塊
       
 
  
  
 bzoj4564: [Haoi2016]地圖 
 Description 
 一天rin來到了一個遙遠的都市。這個都市有n個建築，編號從1到n，其中市中心編號為1，這個都市有m條雙向通 行的街道，每條街道連線著兩個建築，其中某些街道首尾相連連線成了一個環。rin通過長時間的走訪，已經清楚 

  
 

    

    
    UOJ#23. 【UR #1】跳蚤國王下江南 仙人掌 Tarjan 點雙 圓方樹 點分治 多項式 FFT
      原文連結https://www.cnblogs.com/zhouzhendong/p/UOJ23.html 
題目傳送門 - UOJ#23 
題意 
　　給定一個有 n 個節點的仙人掌（可能有重邊）。 
　　對於所有的 $L(1\leq L\leq n-1)$ ，求出有多少不同的從節點 1 出發的包含 L 條 

  
 

    

    
    批處理命令學習筆記——簡單的批處理應用例項
      
                (1) 利用 FOR 迴圈掃描 IP 地址
下面的命令使用了4個FOR巢狀，用法為：“C:\>TEST.BAT <網路地址>”。

for /l %%a in (0,1,255) do for /l %%b in (0,1,255) do (
    for 

  
 

    

    
    圖論雜項細節梳理&模板（虛樹，圓方樹，仙人掌，還有。。。）
      準備   while   class   www   哪裏   容易   return   mes   模板   虛樹
%自為風月馬前卒巨佬%
用於優化一類樹形DP問題。
當狀態轉移只和樹中的某些關鍵點有關的時候，我們把這些點和它們兩兩之間的LCA弄出來，以點的祖孫關系連成一棵新的樹，這就是虛樹。
容易證明， 

  
 

    

    
    ## vue學習筆記--簡單父子組件--
      his   scrip   變量   event   cli   通訊   按鈕   itl   事件   ## vue學習筆記
### 組件之間的通訊1. 父組件到子組件```js    //father    <div>        <son msg="父組件的信息寫在這">&l 

  
 

    

    
    《機器學習》第三章 決策樹學習  筆記加總結
      分類問題   子集   觀察   組成   cas   普通   重復   1.0   需要   《機器學習》第三章 決策樹學習
決策樹學習方法搜索一個完整表示的假設空間，從而避免了受限假設空間的不足。決策樹學習的歸納偏置是優越選擇較小的樹。
3.1.簡介
決策樹學習是一種逼近離散值目標函數的方法，在這種方法 

  
 

    

    
    PHP學習筆記-簡單的面向過程寫的驗證碼
      php<?php
/**
 * Created by PhpStorm.
 * User: Administrator
 * Date: 2017\10\10 0010
 * Time: 19:44
 */
 
//生成隨機驗證碼
$strNumber = join(‘‘,range(0,9));
$s 

  
 

    

    
    斯坦福2014機器學習筆記七----應用機器學習的建議
      訓練集   image   是的   bsp   推斷   學習曲線   正則   偏差   wid   一、綱要
　　糾正較大誤差的方法
　　模型選擇問題之目標函數階數的選擇
　　模型選擇問題之正則化參數λ的選擇
　　學習曲線
二、內容詳述
　　1、糾正較大誤差的方法
　　當我們運用訓練好了的模型來做預測時

仙人掌&圓方樹學習筆記+簡單應用