以後會逐漸完善，現在會先存放一些程式碼

廣義圓方樹對於每個仙人掌的環新建一個方點，原仙人掌上的點為圓點，向這個環上的所有圓點連邊，使得所有的邊連線的都是 $ 1 $ 個圓點和 $ 1 $ 個方點

廣義圓方樹長這個樣子

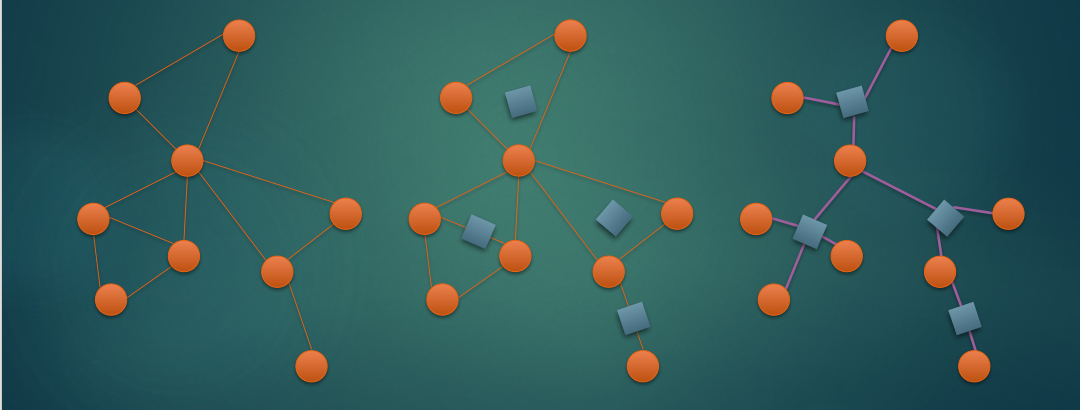
然後就可以用樹形 dp 的方法來解決很多仙人掌上的問題啦

bzoj 4316（求仙人掌最大獨立集

建出圓方樹，進行樹形 dp

對於圓點 $ i $，記 $ f_{i,0} $ 表示不選取 i，i 子樹的最大獨立集，$ f_{i,1} $ 表示 $ i $ 子樹的最大獨立集

然後要注意一下在原仙人掌上有連邊的兩個點不能同時選

如一個方點的父親不能和它在原圖裡連的兩個圓點同時選

感覺這個 dp 也不是很煩

#include <bits/stdc++.h>
#define CIOS ios::sync_with_stdio(false);
#define rep(i, a, b) for(register int i = a; i <= b; i++)
#define per(i, a, b) for(register int i = a; i >= b; i--)
#define DEBUG(x) cerr << "DEBUG" << x << " >>> ";
using namespace std;

typedef unsigned long long ull;
typedef long long ll;

template <typename T>
inline void read(T &f) {
    f = 0; T fu = 1; char c = getchar();
    while (c < '0' || c > '9') { if (c == '-') fu = -1; c = getchar(); }
    while (c >= '0' && c <= '9') { f = (f << 3) + (f << 1) + (c & 15); c = getchar(); }
    f *= fu;
}

template <typename T>
void print(T x) {
    if (x < 0) putchar('-'), x = -x;
    if (x < 10) putchar(x + 48);
    else print(x / 10), putchar(x % 10 + 48);
}

template <typename T>
void print(T x, char t) {
    print(x); putchar(t);
}

const int N = 1e5 + 5;

vector <int> a[N], b[N];
int low[N], dfn[N], f[N][2], tmp[N][2], st[N], top;
int n, m, oldn, _time;

void tarjan(int u) {
    st[++top] = u; low[u] = dfn[u] = ++_time;
    for(register int i = 0; i < a[u].size(); i++) {
        int v = a[u][i];
        if(!dfn[v]) {
            tarjan(v);
            low[u] = min(low[u], low[v]);
            if(low[v] >= dfn[u]) {
                int tmp = 0; ++n;
                while(tmp != v) {
                    tmp = st[top--];
                    b[n].push_back(tmp);
                    b[tmp].push_back(n);
                }
                b[u].push_back(n);
            }
        } else low[u] = min(low[u], dfn[v]);
    }
}

void dfs(int u, int fa) {
    if(u <= oldn) {
        f[u][0] = 0; f[u][1] = 1;
        for(register int i = 0; i < b[u].size(); i++) {
            int v = b[u][i]; if(v == fa) continue; dfs(v, u);
            f[u][0] += f[v][1]; f[u][1] += f[v][0];
        }
        f[u][1] = max(f[u][1], f[u][0]);
    } else {
        for(register int i = 0; i < b[u].size(); i++) dfs(b[u][i], u);
        tmp[0][0] = tmp[0][1] = f[b[u][0]][0];
        for(register int i = 1; i < b[u].size(); i++) {
            int v = b[u][i];
            tmp[i][0] = tmp[i - 1][1] + f[v][0];
            tmp[i][1] = tmp[i - 1][0] + f[v][1];
            tmp[i][1] = max(tmp[i][1], tmp[i][0]);
        }
        f[u][0] = tmp[b[u].size() - 1][0];
        tmp[0][0] = f[b[u][0]][0]; tmp[0][1] = f[b[u][0]][1];
        for(register int i = 1; i < b[u].size(); i++) {
            int v = b[u][i];
            tmp[i][0] = tmp[i - 1][1] + f[v][0];
            tmp[i][1] = tmp[i - 1][0] + f[v][1];
            tmp[i][1] = max(tmp[i][1], tmp[i][0]);
        }
        f[u][1] = tmp[b[u].size() - 1][1];
    }
}

int main() {
    read(n); read(m); oldn = n;
    for(register int i = 1; i <= m; i++) {
        int u, v; read(u); read(v);
        a[u].push_back(v);
        a[v].push_back(u); 
    }
    tarjan(1); dfs(1, 0);
    print(f[1][1], '\n');
    return 0;
}

// Rotate Flower Round.