迴圈序列模型——05.序列模型第一週課程筆記
阿新 • • 發佈:2018-11-26
一、為什麼使用序列模型
能處理非固定大小輸入的問題,例如語音識別,DNA序列分析,機器翻譯這種是一串序列的問題。
二、 數學符號表示
以自然語言處理為例:
x: Harry Potter and Hermione Granger invented a new spell.
以這句話為輸入x,希望得到一個相同長度的y,判斷每個單詞是否表示人名。
首先需要構建一個按字母排序的單詞詞典,當然該詞典中包含單詞的個數因網路和計算資源的不同而不同,一般有4000個等,在這裡我們為了表示方便,假設單詞數量為1000。然後將每個單詞對應在字典中的位置,對映成一個長度為1000的一維向量(onehot)。具體表示方法如下所示:
| 符號 | 說明 |
|---|---|
| 表示該句話的第 個單詞,在此處表示Harry在詞典中序號為4。 | |
| 表示第 個單詞的輸出。 | |
| 這個序列的長度為9 | |
| 這個序列的輸出長度為9 | |
| 樣本中第 個序列的第 個單詞 | |
| 樣本中第 個輸入序列的長度 |
注意:如果樣本中出現了詞典中不包含的單詞,需要定義一個Unknown向量,以及每句話的結尾EOS向量。
三、迴圈神經網路模型
1 為什麼不能用標準的神經網路
- 在序列輸入問題中,大部分的輸入不能輸出都不能統一
- 在同一個單詞在文字的不同位置不能分享特徵
2 迴圈神經網路
2.1 前向傳播
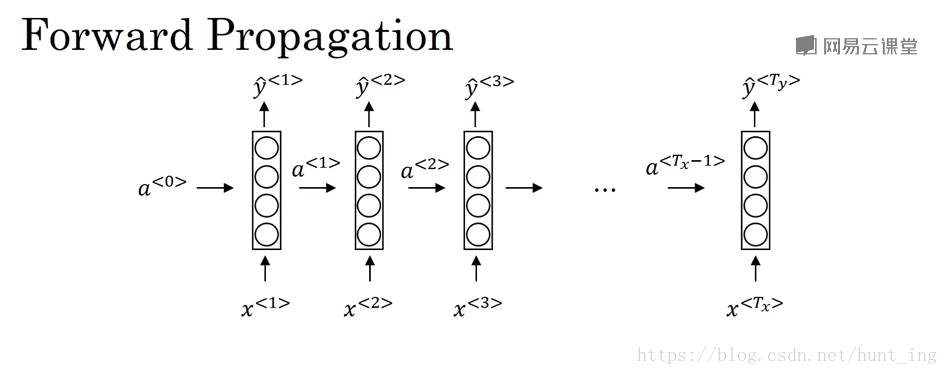
公式可以簡化為
2.2 方向傳播
對於一個判斷是否為人名的二分類問題,可以定義損失函式:
通過梯度下降演算法不斷更新引數
時間反向傳播(backpropagation through time)
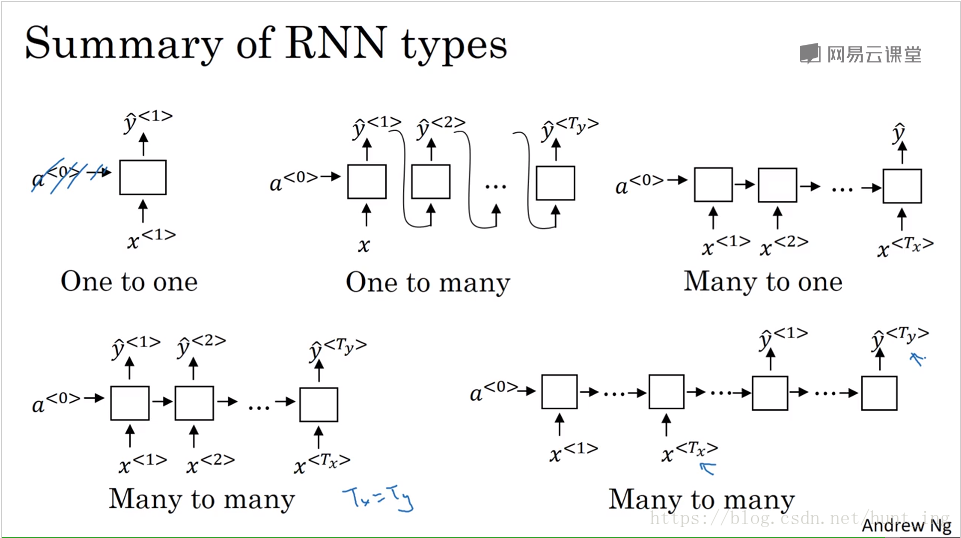
2.3 不同型別的迴圈神經網路
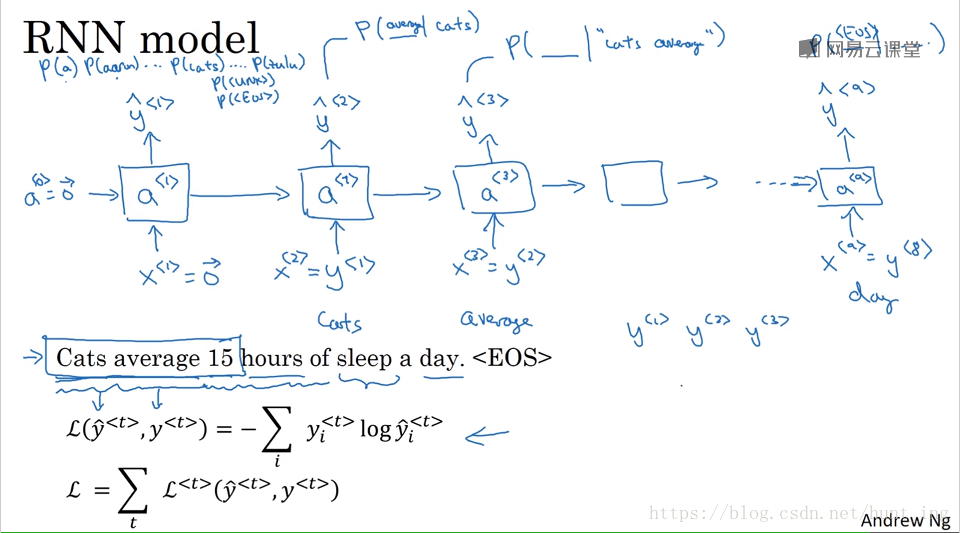
3 語言模型和序列生成
3.1 生成過程
一句話概括就是:單詞出現的概率。
需要訓練集:一個大的語料庫(corpus of English text 數量眾多的句子)
3.2 生成取樣
通過每個單元生成的softmax概率,然後以每個單詞的概率做隨機,到第二個單元時以第一個單元的結果為輸入,然後再生成softmax概率,如此迴圈直到生成EOS標誌或者限定時間數。
3.3 字元模型
相比較詞彙模型