BiLSTM+CRF

現在比較流行的是bilstm+crf，即在bilstm後面接了crf層

• 經過bilstm得到隱狀態序列 $(h_1,h_2$
  , . . . , h n ) ∈
  R n ∗ m (h_1,h_2,...,h_n) \in R^{n*m}
• 接入一個線性層，轉換隱狀態序列的維度，從 $m$
  m 維轉換到 $k$維， $k$是標籤數。我們可以理解這一步是由網路自動學習當前單詞對應到每個標籤的分數。
• 接下來是CRF層，這一層需要學得的引數是 $(k+2)*(k+2)$的矩陣T，此處考慮了start和end標籤， $T_{ij}$表示從標籤 $i$到標籤 $j$的轉移得分。可以看出通過新增CRF考慮了標籤之間的關係

這裡提到接上CRF層，和真正的CRF是不同的，不要混淆

資料：

• tensorflow之bilstm+crf程式碼簡析
  https://blog.csdn.net/guolindonggld/article/details/79044574
• bilstm+crf原理簡析
  https://www.cnblogs.com/Determined22/p/7238342.html
• 對lstm+crf實現的細緻解析
  https://createmomo.github.io/2017/11/11/CRF-Layer-on-the-Top-of-BiLSTM-5/

CRF

生成式模型與判別式模型
1）生成式模型：直接對聯合概率進行建模，比如：GMM, HMM,NB
2) 判別式模型：對條件概率進行建模，比如：CRF, MEMM

概率無向圖模型

概率無向圖模型又稱馬爾可夫隨機場或馬爾可夫網路，是一個可以由無向圖表示的聯合概率分佈。該聯合分佈滿足成對/區域性/全域性馬爾可夫性。

概率有向圖模型又稱貝葉斯網路。
我們如何把貝葉斯網路轉換為馬爾可夫網路呢？
第一步：將節點的父節點兩兩進行連線
第二步：去掉箭頭

如何計算聯合概率：因子分解
概率無向圖模型的聯合概率為：圖中所有最大團上的隨機變數的函式的乘積，然後進行歸一化
$P(Y) = \frac{1}{Z} \prod\limits_C \psi_C(Y_C)$
其中 $Z = \sum\limits_Y \prod\limits_C \psi_C(Y_C)$，是歸一化因子。 $\psi_C(Y_C)$是C上定義的嚴格正函式，被稱作勢函式。

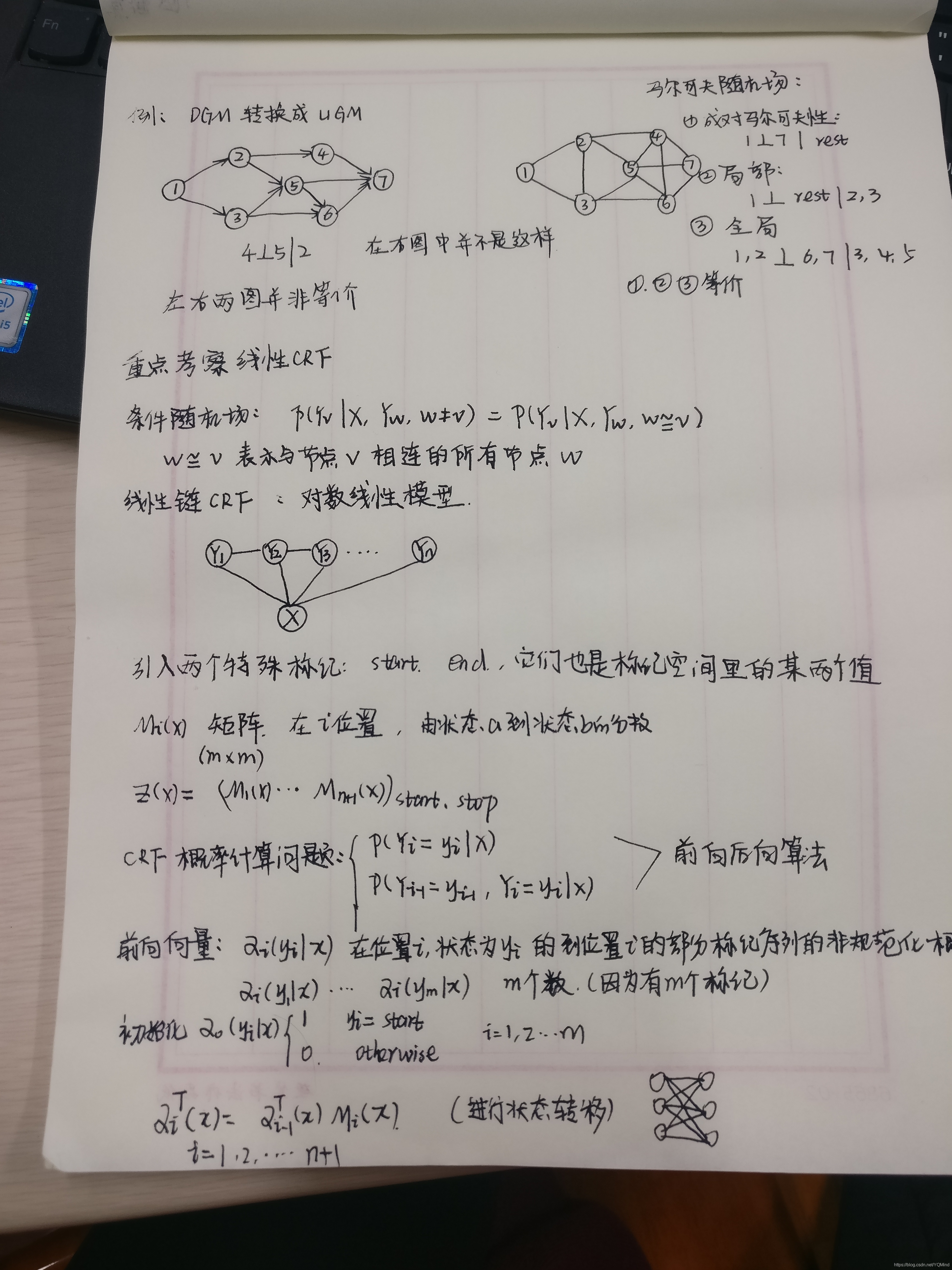
線性鏈CRF
條件概率P(Y|X), X是句子，Y是標註序列。條件隨機場是給定X條件下，Y滿足馬爾可夫性(Y是馬爾可夫隨機場)。
簡單來說，有多個特徵模板。每個特徵模板都要滑過每個位置，相加起來，得到該特徵模板對整個句子的一個打分。然後對多個特徵模板加權求和。
引數化形式：
$p(y|x) = \frac{1}{Z(x)}exp(\sum\limits_{i,k} \lambda_kt_k(x,i,y_{i-1},y_i) + \sum\limits_{i,l}\mu_ls_l(x,i,y_i))$
從這個式子，我們可以看出，線性鏈CRF中有兩類特徵函式，邊上的特徵函式（轉移特徵）、點上的特徵函式（狀態特徵）。

因此在有的地方，你可能會看到其他人並不是這樣的引數化形式。他們做了一定了簡化，即將這兩類特徵函式用一個形式表達了。你只需要記住有這兩類特徵函式就可以了，邊和點。

還有一點需要注意，特徵函式都是人為設計的，因此線上性鏈CRF中需要學習的引數是，每個特徵函式對應的權重，即 $\lambda_k, \mu_l$

學習過程中的有點混亂的筆記

感想：
CRF的資料看了很多，而且大部分都是捏來的李航老師的《統計機器學習》，不得不說自己一次次懷疑自己，怎麼就看不懂呢？
堅持看下去之後，我認為理解CRF的三個問題關鍵在於：

1. 對CRF的引數化形式要十分熟悉，而且要靈活變換。本質是不變的，但是應用的形式是可以變化的
2. CRF同樣具有HMM中的三個問題：概率估計問題、引數學習問題和預測問題。其中概率估計問題使用前向後向演算法，預測問題使用維特比演算法，這兩個問題的思路和HMM是一樣的，這就考察你的學習遷移能力啦