原題

題目描述
現在有一個圓圈，圓圈上有若干個點，請判斷能否在若干個點中選擇三個點兩兩相連組成一個等邊三角形？
這若干個點在圓圈上按順時針順序分佈。
如果可以的話輸出"Yes"(不含引號)
不可以的話輸出"No"(不含引號)

輸入
第一行一個整數n，表示圓圈上有n個點
第二行n個整數，分別表示第1個點與第2個點之間圓弧的長度、第2個點與第3個點之間圓弧的長度······第n個點與第1個點之間圓弧的長度
3 <= n <= 10^6
1 <= x_i <= 1000 ( 1 <= i <= n)

輸出
如果可以組成等邊三角形則輸出"Yes"(不含引號)
否則輸出"No"(不含引號)

樣例輸入
樣例輸入1：
4
1 1 2 2

樣例輸入2：
8
4 2 4 2 2 6 2 2

樣例輸出
樣例輸入1：
Yes

樣例輸入2：
Yes

提示
對於樣例2配圖：

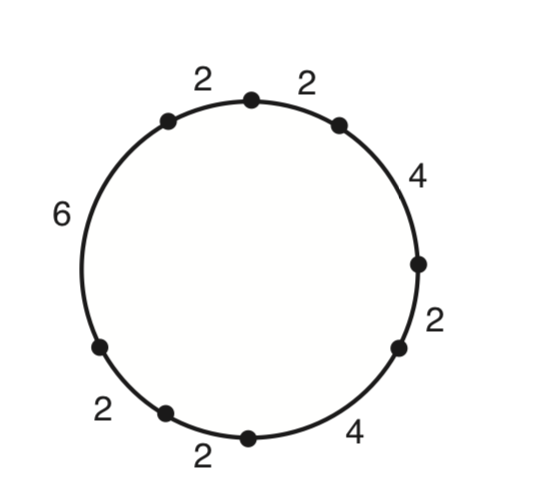
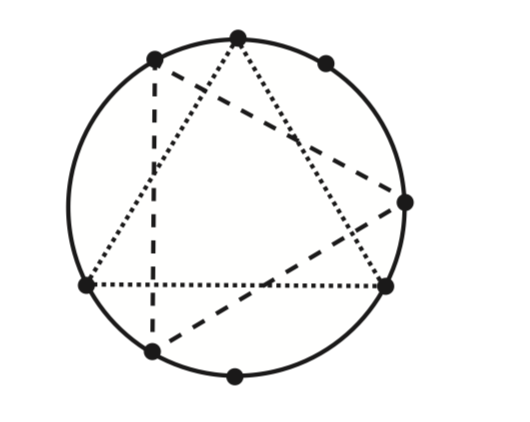
感慨

又一次被題目嚇破了膽。。。實際上這個題還是挺簡單的(看了凱哥的題解。。）

解法

①既然要找到圓內是否有等邊三角形，那麼就應該從等邊三角形的性質入手，如果為等邊三角形那麼這三個三角形的頂點一定三等分圓弧

②有了①的結論那麼這個題就好做多了。首先我們可以把圓看成一條直線，圓上的點可以對映為直線上的點，二維變一維

③之後我們把每個出現的點都用桶去記錄，這裡好像因為資料大小的問題還是開map比較保險，畢竟re還是罰時不少的

④然後記錄每一個點的座標，再記錄好三等分圓弧的量，然後尋找是否有這樣的點即可

⑤這裡有一個小結論就是如果直線的長度%3不等於0的話，那麼可以直接判斷為沒有，不過資料好像不強這個地方沒有考慮到

程式碼

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/hash_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
typedef long long ll;
gp_hash_table <ll,ll> bk,x;
ll pt,n;
int main()
{
  ios::sync_with_stdio(0);
  cin.tie(0);
  cout.tie(0);
  cin>>n;
  for(int i=0;i<n;i++)
  {
    int t;
    cin>>t;
    bk[pt]=1;
    x[i]=pt;
    pt+=t;
  }
  if(pt%3!=0)
  return cout<<"No",0;
  ll r=pt/3;
  for(int i=0;i<n;i++)
  {
    ll x1=x[i]+r;
    ll x2=x[i]+r+r;
    if(bk[x1]&&bk[x2])
    return cout<<"Yes",0;
    if(x1>=pt||x2>pt)
    break;
  }
  cout<<"No";
}