習題4.1

1.擺渡的士兵 n個士兵組成的分隊必須越過一條又深又寬又沒有橋的河。他們注意到在岸旁有兩個12歲大的小男孩在玩划艇。然而船非常小，只能容納兩個男孩或一名士兵。怎樣才能讓士兵渡過河，並且留下兩個男孩操縱這條船？這條船要在岸與岸之間橫渡多少次？

解答：每次只能容納一名士兵，所以士兵一定是一個一個過河，同時需要有小男孩將船劃回來，那麼每一次士兵過河之前，兩個小男孩先划船過去，然後一個小男孩划船回來，另一個小男孩在士兵過河之後把船劃回來。所以擺渡n個士兵，需要執行這樣的步驟n次，每次船在岸與岸之間橫渡4次，共4n次。

2.交替放置的玻璃杯 有2n個玻璃杯挨個排成一行，前n個裝滿蘇打水，其餘n個杯子為空。交換杯子的位置，使之按照一空一滿一空(filled-empty-filledempty pattern

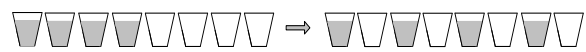
解答：給2n個杯子從左至右從1開始依次編號，將第2個杯子與第n-1個杯子互換，那麼此問題轉化為2(n-2)個杯子的問題。交換次數M(n)=M(n-2)+1,當n>2時; M(1)=0;M(2)=1.

3.標記單元格 為下列任務設計一個演算法。n為任意偶數，在一張無限大的繪圖個字紙上標記n個單元格，使得每個被標記的單元格有奇數個相鄰的標記單元格。相鄰是指兩個單元格在水平方向兩個單元格在水平方向或垂直方向上相鄰，但非對角方向上相鄰。被標記的單元格必須形成連續域，也就是說區域中任意一對標記單元格之間有一條經過一系列相鄰標記單元格的路徑。

解答：根據題意，以下列出了n=2,4,6的標記結果，每增加兩個標記格，則只能在水平方向（該方向可任意指定）增加一個單元格，在豎直方向交替增加一個單元格，只有這樣才能滿足題目要求。

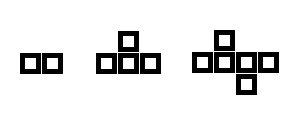
6.隊伍排序 給定一個完全迴圈賽的比賽結果，其中n個隊伍兩兩比賽一次。每場比賽以一方勝出或者平局結束。設計一個演算法，把n個隊伍排序，序列中每個隊伍都不曾輸給緊隨其後的那個隊。說明該演算法的時間效率型別。

解答：以任意一個隊伍初始化所求序列，然後將其他隊伍依次插入該序列。插入過程中，將當前隊伍與序列中的隊伍從前到後一一比較，若找到勝利或者平局的隊伍，則插入到該隊伍的前方，否則會一直比較，直到最後插入隊伍末端。該演算法的效率型別為O(n2)，最差情況下每次插入時都位於隊伍最末端。

習題4.2

10.蛛網問題 一隻蜘蛛位於網的底端(S)，而一隻蒼蠅位於網的頂端(F)。沿著箭頭方向在線上移動，蜘蛛有多少不同的路徑到達蒼蠅處？

解答：從S出發按照拓撲排序的順序依次遍歷節點，對每個節點計算從S出發到達它存在多少路徑，計算方法是對所有前驅節點的路徑數求和。計算得到到達F節點的路徑數是141。

習題4.3

11.格雷碼和漢諾塔

a. 為什麼漢諾塔的經典遞迴演算法產生的移動盤子動作可以用來生成二進位制反射格雷碼？

解答：題目原文：Show that the disk moves made in the classic recursive algorithm for the Tower-of-Hanoi puzzle can be used for generating the binary reflected Gray code.

定義從小到大的盤子序號分別為1，2，……n，初始化一個全為0的n位序列，m號盤子對應從右到左的第m位，每次移動一個盤子，則該位的元素翻轉，構成二進位制反射格雷碼的一個序列。

b. 如何利用二進位制反射格雷碼來解決漢諾塔問題？

解答：在生成格雷碼的演算法中，依次改變的位數是最低位和從右往左數第一個1所在位的左一位，對應漢諾塔的盤子就是最小的盤子和中間某個盤子。最小的盤子有兩種可能的移動方案，其他的盤子只有一種可能。對於最小盤子移動到的柱子的解決方法是，根據觀察，當盤子總數是奇數時，最小盤子的位置依次是“3->2->1->3->2->1...”；當總數是偶數時，這個順序是“2->3->1->2->3->1...”。據此從格雷碼到漢諾塔的一種對應解決方案就產生了。

12.展會彩燈 早些年，在展會上可能會看到這樣一種彩燈：一個被連線到若干開關上的電燈泡，只當所有開關閉合的時候才會發光。每一個開關由一個按鈕控制；按下按鈕就會切換開關狀態，但是開關的狀態是無法知道的。目標就是點亮燈泡。設計一個點亮燈泡的演算法，使其在有你n個開關時，在最壞的情況下，需要按動按鈕的次數最少。

解答：可以利用二進位制反射格雷碼的特性，相鄰兩個位串只相差一位數字，而2n個位串都是不同的。將n個開關分別對應n位二進位制格雷碼的每一位，每當格雷碼的序列某一位發生變化，切換對應的開關狀態。

習題4.4

7.猜圖片 一個非常流行的解題遊戲是這樣的：給選手出示42張圖片，每行6張，共7行。選手可以給大家做一些是非題，來確定他要尋找的圖片。然後進一步要求選手用盡可能少的問題來確定目標圖片。給出解決問題的最有效的演算法，並指出需要提問的最大次數。

解答：把42張圖片依次標號，用二分查詢方法，比如第一個問題是“目標圖片的序號是不是大於21？”，所需提問的最大次數是

10.a.為假幣問題的三分演算法寫一段虛擬碼。請確保該演算法會正確處理所有的n值，而不僅僅是那些3的倍數。

解答： 每次平均分三堆的結果可能有：餘數0、餘數1、餘數2

如果餘數0：平均分，任選兩堆（堆1+堆2）比較，如果平衡：堆3含假幣；如果不平衡：比較堆1和堆3，如果平衡：堆2含假幣；如果不平衡：堆1含假幣；

餘數1:平均分後得到3堆+1個硬幣，任選兩堆（堆1+堆2）比較，如果平衡：比較堆1和堆3，如果平衡：剩餘的單個硬幣為假，如果不平衡：堆3為含假幣的堆如果不平衡：比較堆1和堆3，如果平衡：堆2含假幣；如果不平衡：堆1含假幣

餘數2:平均分後得到3堆+2個硬幣，任選兩堆（堆1+堆2）比較，如果平衡：比較堆1和堆3，如果平衡：假幣在兩個單個硬幣中，這兩個硬幣必然是不平衡的，這時從堆中找出任意一枚硬幣，從兩個單個硬幣中拿出硬幣1進行比較，如果平衡：假幣為幣2；如果不平衡，假幣為幣1；如果堆1和堆3不平衡：堆3為含假幣的堆，如果不平衡：比較堆1和堆3，如果平衡：堆2含假幣；如果不平衡：堆1含假幣。

b.為假幣問題的三分演算法的稱重次數建立一個遞推關係，並在n=3k的情況下對它求解。

解答：稱重次數W(n)=W( )+1,當n>1;W(1)=0。當n=3k，W(3k)=W(3k-1)+1，解得W(3k)=k=log3n。

c.當n的值非常大時，該演算法要比把硬幣分成兩堆的演算法快多少倍？這個答案應該與n無關。

解答：

習題4.5

10.另類單堆拈遊戲 請考慮這個另類的單堆拈遊戲，它規定誰拿走最後一個棋子就輸了。該遊戲的其他條件都不變，即該堆棋子有n個，每次每個玩家最多拿走m個，最少拿走1個棋子。請指出該遊戲的勝局和敗局是怎樣的？

分析：當n=1，先拿的人輸；當2<=n<=m+1,先拿的人選擇n-1個棋子拿走能夠贏；當n=m+2，先拿的人會輸……以此類推。

解答：敗局是n mod (m+1) = 1，勝利的策略是每次拿走(n-1) mod (m+1)的棋子。

11.壞巧克力 兩個玩家輪流掰一塊m×n格的巧克力，其中一塊1×1的小塊是壞的。每次掰只能順著方格的邊界，沿直線一掰到底，每掰一次，掰的人把兩塊中不含壞巧克力的那塊吃掉，誰碰到最後那塊塊巧克力就算輸了。在這個遊戲中，先走好還是後走好？

解答：相當於多堆拈遊戲，每邊到達壞巧克力塊的距離就是一堆，然後用二進位制數位和計算。

寫一個互動程式，讓大家可以和這個計算機玩這個遊戲。這個程式在勝局應該走出致勝一步，在敗局中則只要隨機下出合理的一步即可。

#include<iostream>  
//巧克力大小  
#define M 8  
#define N 8  
  
//設定壞巧克力塊的位置  
#define X  4  
#define Y  4  
  
void print(char cho[M][N])  
{  
    //打印出巧克力形狀  
    for (int i = 0; i<M; i++)  
    {  
        for (int j = 0; j<N; j++)  
            printf("%d ", cho[i][j]);  
        printf("\n");  
    }  
}  
//執行掰巧克力的函式  
void Execute(char cho[M][N], char pos, int index)  
{  
    //掰下一列  
    if (pos == 'C' || pos == 'c')  
    {  
        for (int i = 0; i<M; i++)  
        {  
            for (int j = 0; j<N; j++)  
                if (j == index)cho[i][j] = 3;  
        }  
    }  
    //掰下一行  
    else if (pos == 'R' || pos == 'r')  
    {  
        for (int i = 0; i<M; i++)  
        {  
            if (i == index)  
            {  
                for (int j = 0; j<N; j++)cho[i][j] = 3;  
            }  
        }  
    }  
}  
//分析行，給出決策可以掰那些行  
void Row(char cho[M][N], char dm[])  
{  
    for (int i = 0; i<M; i++)  
    {  
        int s = -1;  
        //去掉壞巧克力所在行  
        if (i != X)  
        {  
            for (int j = 0; j<N; j++)  
            {  
                if (cho[i][j] != 3)s = 1;  
            }  
        }  
        dm[i] = s;  
    }  
}  
//分析列，給出決策可以掰那些列  
void Col(char cho[M][N], char dm[])  
{  
    for (int j = 0; j<N; j++)  
    {  
        int s = -1;  
        //去掉壞巧克力所在列  
        if (j != Y)  
        {  
            for (int i = 0; i<M; i++)  
            {  
                if (cho[i][j] != 3)s = 1;  
            }  
        }  
        dm[j] = s;  
    }  
}  
  
//預處理，計算機模擬執行掰的過程，然後計算剩餘步驟  
int PreDispose(char cho[M][N], char dm[])  
{  
    int cnt = 0;  
    //巧克力塊的副本  
    char cho_t[M][N];  
  
    //可以掰的行標，用1表示  
    char row[M];  
    //可以掰的列表，用1表示  
    char col[N];  
    memset(row, -1, M); memset(col, -1, N);  
  
    memcpy(cho_t, cho, M*N);  
    Execute(cho_t, dm[0], dm[1]);  
  
    //分析行，給出決策  
    Row(cho, row);  
    //分析列，給出決策  
    Col(cho, col);  
  
    for (int i = 0; i<M; i++)  
        if (row[i] != -1)cnt++;  
    for (int j = 0; j<N; j++)  
        if (col[j] != -1)cnt++;  
  
    return cnt;  
}  
  
//分析現在的巧克力,並給出決策，掰哪一塊  
void Alaysize(char cho[M][N], char dm[2])  
{  
    //可以掰的行標，用1表示  
    char row[M];  
    //可以掰的列表，用1表示  
    char col[N];  
  
    memset(row, -1, M); memset(col, -1, N);  
  
    //分析行，給出決策  
    Row(cho, row);  
    //分析列，給出決策  
    Col(cho, col);  
  
  
    //進行預處理，判斷執行後的剩餘次數,找到一個剩餘次數為奇數的步驟執行  
    for (int i = M - 1; i >= 0; i--)  
    {  
        if (row[i] != -1)  
        {  
            dm[0] = 'R';  
            dm[1] = i;  
            if (PreDispose(cho, dm) % 2 != 0)  
            {  
                printf("找到最佳步驟:\n");  
                return;  
            }  
        }  
    }  
    for (int j = N - 1; j >= 0; j--)  
    {  
        if (col[j] != -1)  
        {  
            dm[0] = 'C';  
            dm[1] = j;  
            if (PreDispose(cho, dm) % 2 != 0)  
            {  
                printf("找到最佳步驟:\n");  
                return;  
            }  
        }  
    }  
    //如果沒有最佳步驟，則隨便走一步  
    return;  
}  
  
//計算機掰巧克力的過程  
void Computer(char cho[M][N])  
{  
    char dm[2];  
    dm[0] = -1; dm[1] = -1;  
    //讓計算機開始分析巧克力，並給出決策  
    Alaysize(cho, dm);  
    printf("計算機給出決策 %c %d\n", dm[0], dm[1]);  
    if (dm[0] == -1 && dm[1] == -1)  
    {  
        printf("計算機輸了\n");  
    }  
    //掰巧克力  
    Execute(cho, dm[0], dm[1]);  
}  
  
int main()  
{  
    //製作巧克力  
    char cho[M][N];  
  
    char pos[10];  
  
    char cmd = 0;  
    int index = 0;  
  
    //設定壞巧克力  
    memset(cho, 0, M*N);  
    cho[X][Y] = 1;  
  
    //列印巧克力  
    print(cho);  
  
    printf("請輸入命令:\n");  
    scanf("%s", pos);  
  
    while (1)  
    {  
        cmd = pos[0];  
        index = atoi(pos + 1);  
  
        if (cmd == 'Q' || cmd == 'q')break;  
  
        //掰巧克力  
        Execute(cho, cmd, index);  
        //打印出巧克力形狀  
        print(cho);  
  
        //計算機處理  
        Computer(cho);  
        //打印出巧克力形狀  
        print(cho);  
  
        printf("請輸入命令:\n");  
        scanf("%s", pos);  
    }  
  
    return 0;  
}  

12.翻薄餅 有n張大小各不相同的薄餅，一張疊在另一張上面。允許大家把一個翻板插到一個薄餅下面，然後可以把板上面這疊薄餅翻個身。我們的目標是根據薄餅的大小重新安排它們位置，最大的薄餅要放在最下面。設計一個演算法來解這個謎題。

解答：找到最大的薄餅，先將它翻到頂，然後全部翻過來。這樣最大的薄餅就位於最下方，問題轉化成將第二大的薄餅放在下方第二個位置。採用減治法（減一）思想，不斷地執行該步驟。