python數據結構與算法(8)
阿新 • • 發佈:2018-11-28
sel 是否為空 earch pen klist term ado append shadow 鏈表與順序表的對?
鏈表失去了順序表隨機讀取的優點,同時鏈表由於增加了結點的指針域,空 間開銷?較?,但對存儲空間的使?要相對靈活。
鏈表與順序表的各種操作復雜度如下所示:
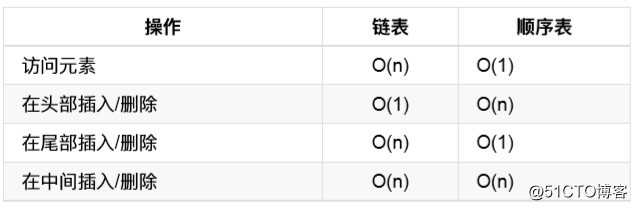
註意雖然表?看起來復雜度都是 O(n),但是鏈表和順序表在插?和刪除時進 ?的是完全不同的操作。鏈表的主要耗時操作是遍歷查找,刪除和插?操作 本身的復雜度是O(1)。順序表查找很快,主要耗時的操作是拷?覆蓋。因為 除了?標元素在尾部的特殊情況,順序表進?插?和刪除時需要對操作點之 後的所有元素進?前後移位操作,只能通過拷?和覆蓋的?法進?。
鏈表失去了順序表隨機讀取的優點,同時鏈表由於增加了結點的指針域,空 間開銷?較?,但對存儲空間的使?要相對靈活。
鏈表與順序表的各種操作復雜度如下所示:

註意雖然表?看起來復雜度都是 O(n),但是鏈表和順序表在插?和刪除時進 ?的是完全不同的操作。鏈表的主要耗時操作是遍歷查找,刪除和插?操作 本身的復雜度是O(1)。順序表查找很快,主要耗時的操作是拷?覆蓋。因為 除了?標元素在尾部的特殊情況,順序表進?插?和刪除時需要對操作點之 後的所有元素進?前後移位操作,只能通過拷?和覆蓋的?法進?。
雙向鏈表
?種更復雜的鏈表是“雙向鏈表”或“雙?鏈表”。每個節點有兩個鏈接:?個指 向前?個節點,當此節點為第?個節點時,指向空值;?另?個指向下?個 節點,當此節點為最後?個節點時,指向空值。
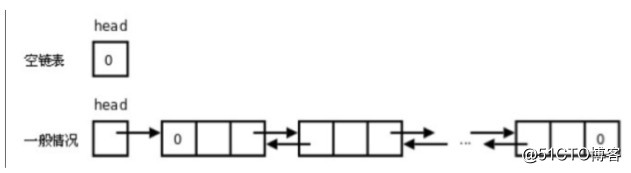
操作
is_empty() 鏈表是否為空 length() 鏈表?度 travel() 遍歷鏈表 add(item) 鏈表頭部添加 append(item) 鏈表尾部添加 insert(pos, item) 指定位置添加 remove(item) 刪除節點 search(item) 查找節點是否存在
實現
class Node(object): """雙向鏈表節點""" def __init__(self, item): self.item = item self.next = None self.prev = None class DLinkList(object): """雙向鏈表""" def __init__(self): self.__head = None def is_empty(self): """判斷鏈表是否為空""" return self.__head == None def length(self): """返回鏈表的?度""" cur = self.__head count = 0 while cur != None: count += 1 cur = cur.next return count def travel(self): """遍歷鏈表""" cur = self.__head while cur != None: print cur.item, cur = cur.next print "" def add(self, item): """頭部插?元素""" node = Node(item) if self.is_empty(): # 如果是空鏈表,將_head指向node self.__head = node else: # 將node的next指向_head的頭節點 node.next = self.__head # 將_head的頭節點的prev指向node self.__head.prev = node # 將_head 指向node self.__head = node def append(self, item): """尾部插?元素""" node = Node(item) if self.is_empty(): # 如果是空鏈表,將_head指向node self.__head = node else: # 移動到鏈表尾部 cur = self.__head while cur.next != None: cur = cur.next # 將尾節點cur的next指向node cur.next = node # 將node的prev指向cur node.prev = cur def search(self, item): """查找元素是否存在""" cur = self.__head while cur != None: if cur.item == item: return True cur = cur.next return False
python數據結構與算法(8)
